Hüllkurvendemodulation

Inhaltsverzeichnis

1 Funktionsweise bei idealen Bedingungen
2 Realisierung eines Hüllkurvendemodulators (1)
3 Realisierung eines Hüllkurvendemodulators (2)
4 Anwendung der Hüllkurvendemodulation bei $m > 1$

Funktionsweise bei idealen Bedingungen

Wir gehen zunächst von folgenden Voraussetzungen aus:

Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt.
Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”. Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } =$ 0 gesetzt:

$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$

Der Modulationsgrad sei $m$ ≤ 1. Aus der Definition $m = q_{\rm max}/A_{\rm T}$ folgt somit auch $q(t) + A_{\rm T}$ ≥ 0.
Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen. Mit $H_{\rm K}(f) =$ 1 und $n(t) =$ 0 erhält man somit für das Empfangssignal:

$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$

In dieser Gleichung bezeichnet $a(t)$ die Hüllkurve von $r(t)$ . Die Phasenfunktion $\mathbf{ϕ}(t)$ ist 0.

Ein Hüllkurvendemodulator detektiert die Hüllkurve $a(t)$ seines Eingangssignals $r(t)$ und gibt diese nach Eliminierung des Gleichanteils $A_{\rm T}$ als Sinkensignal aus: $v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$ Die Entfernung des Gleichanteils $A_{\rm T}$ kann beispielsweise durch einen Hochpass realisiert werden, der alle Frequenzen bis auf $f =$ 0 ungehindert passieren lässt.

Sind alle obigen Voraussetzungen erfüllt, so gilt $υ(t) = q(t)$ . Das bedeutet, dass mit einem (idealen) Hüllkurvendemodulator durchaus ein ideales Nachrichtenübertragungssystem realisiert werden kann.

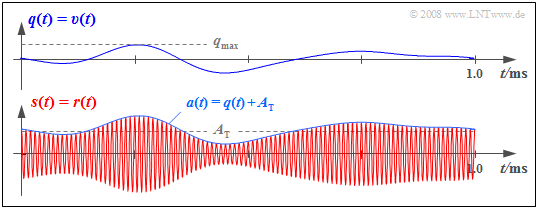
Unten sehen Sie das Empfangssignal $r(t) = s(t)$ , wobei „ZSB–AM mit Träger” zugrunde liegt (Modulationsgrad $m =$ 0.5). Die vom Hüllkurvendemodulator auszuwertende Hüllkurve $a(t)$ ist gleich der Summe aus dem Quellensignal $q(t)$ und dem beim Sender zugesetzten Gleichanteil $A_{\rm T}$ .

Für das Demodulatorausgangssignal nach Eliminierung des Gleichanteils $A_{\rm T}$ mit einem Hochpass gilt $υ(t) = q(t)$ , vorausgesetzt, dass das Quellensignal $q(t)$ keinen Gleichanteil beinhaltet hat. Ein solcher würde durch den Hochpass ebenfalls entfernt.

Realisierung eines Hüllkurvendemodulators (1)

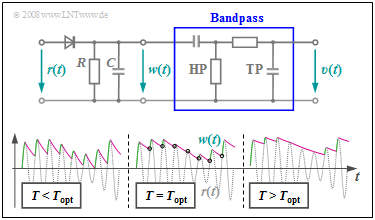
Die nebenstehende Schaltung zeigt eine einfache Realisierungsmöglichkeit des Hüllkurvendemodulators.

Darunter sehen Sie die Signale $r(t)$ und $w(t)$ zur Verdeutlichung des Prinzips.

Betrachten Sie zunächst den mit $T = T_{\rm opt}$ bezeichneten mittleren Signalausschnitt.

Der erste Schaltungsteil – bestehend aus einer Diode und der Parallelschaltung eines Widerstands $R$ und einer Kapazität $C$ – erfüllt folgende Aufgaben:

Ist das grau gezeichnete Signal $r(t)$ größer als die Spannung $w(t)$ an $R$ und $C$ , so leitet die Diode, es gilt $w(t) = r(t)$ und die Kapazität $C$ wird aufgeladen. Diese Bereiche sind grün markiert.
Gilt $r(t) < w(t)$ wie zu den violett markierten Zeiten, so sperrt die Diode und die Kapazität entlädt sich über den Widerstand $R$ . Das Signal fällt exponentiell mit der Zeitkonstanten $T = R · C$ ab.
Ab den mit Kreisen markierten Zeitpunkten gilt wieder $r(t) > w(t)$ und die Kapazität wird wieder aufgeladen. Man erkennt aus der Skizze, dass $w(t)$ in etwa mit der Hüllkurve $a(t)$ übereinstimmt.
Die Abweichungen zwischen $w(t)$ und $a(t)$ sind um so geringer, je größer die Trägerfrequenz im Vergleich zur Nachrichtenfrequenz ist. Als Richtwert wird oft $f_{\rm T} ≥ 100 · B_{\rm NF}$ angegeben.
Gleichzeitig sollte die Zeitkonstante $T$ stets sehr viel größer als $1/f_{\rm T}$ und sehr viel kleiner als $1/B_{\rm NF}$ sein. Ein guter Kompromiss ist das geometrische Mittel zwischen beiden Grenzen:

$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, \hspace{2cm} T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF}}} \hspace{0.05cm}.$

Ist die Zeitkonstante $T$ zu klein wie im linken Bereich obiger Skizze, so wird der Kondensator stets zu schnell entladen und die Differenz $w(t) – a(t)$ unnötig groß.
Auch ein zu großer Wert $T > T_{\rm opt}$ führt zu einer Verschlechterung, wie im rechten Signalausschnitt dargestellt. In diesem Fall kann $w(t)$ der Hüllkurve $a(t)$ nicht mehr folgen.

Bei einer NF–Bandbreite von 5 kHz sollte die Trägerfrequenz mindestens 500 kHz gewählt werden. Die Zeitkonstante $T$ muss sehr viel größer als $1/f_{\rm T} =$ 2 μs und gleichzeitig sehr viel kleiner als $1/B_{\rm NF} =$ 200 μs sein. Der optimale Wert entsprechend der Kompromissformel ist dann: $T_{\rm opt} = {1}/{\sqrt{5 \cdot 10^5 \, {\rm Hz}\cdot 5 \cdot 10^3 \, {\rm Hz}}} = 20 \, \mu s \hspace{0.05cm}.$

Realisierung eines Hüllkurvendemodulators (2)

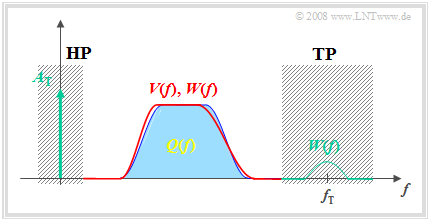
Die folgende Grafik verdeutlicht die Wirkungsweise des Hüllkurvendemodulators im Frequenzbereich:

Das Spektrum $W(f)$ des Signals $w(t)$ an der $RC$ –Parallelschaltung unterscheidet sich vom Spektrum $Q(f)$ des Quellensignals wie folgt:

Aufgrund des beim Sender zugesetzten Trägersignals $z(t)$ beinhaltet die Spektralfunktion $W(f)$ eine Diraclinie bei $f =$ 0 mit dem Gewicht $A_{\rm T}$ (Trägeramplitude).
$W(f)$ weist zudem auch Spektralanteile im Bereich um die Trägerfrequenz $f_{\rm T}$ auf, die sich mit dem gezackten Zeitverlauf $w(t)$ erklären lassen (siehe Grafik im letzten Abschnitt).
Auch im NF–Bereich unterscheidet sich $W(f)$ gegenüber $Q(f)$ geringfügig. Der Fehler wird dabei um so geringer sein, je größer die Trägerfrequenz im Vergleich zur NF-Bandbreite ist.

Während die zwei erstgenannten Signalverfälschungen durch den Hochpass und den Tiefpass eliminiert werden, bleibt die geringfügige Abweichung zwischen dem Sinkensignal $υ(t)$ und dem Quellensignal $q(t)$ im Bereich 0 $< f < B_{\rm NF}$ erhalten, wie aus dem Vergleich von $V(f)$ und $Q(f)$ hervorgeht.

Anwendung der Hüllkurvendemodulation bei $m > 1$

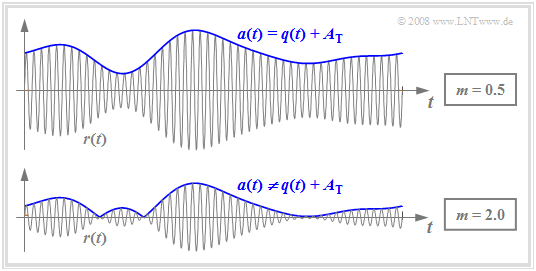
Die nachfolgende Grafik zeigt die ZSB–AM–Signale für $m =$ 0.5 und $m =$ 2.

Aus dieser Darstellung erkennt man folgende Unterschiede:

Solange der Modulationsgrad $m$ ≤ 1 ist, gilt für die Hüllkurve des Bandpass–Signals:

$a(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$

Hier ist mit dem Hüllkurvendemodulator eine ideale Demodulation möglich:

$υ(t) = q(t)$ .

Dagegen gilt bei $m$ > 1 folgender Zusammenhang:

$$