Zweiseitenband-Amplitudenmodulation

Beschreibung im Frequenzbereich (1)

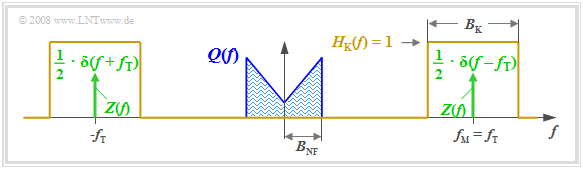
Wir betrachten die folgende Aufgabenstellung: Ein Nachrichtensignal $q(t)$ , dessen Spektrum $Q(f)$ auf den Bereich $\pm B_{\rm NF}$ bandbegrenzt ist, soll mit Hilfe einer harmonischen Schwingung der Frequenz $f_{\rm T}$ , die wir im Weiteren als Trägersignal $z(t)$ bezeichnen, in einen höherfrequenten Bereich verschoben werden, in dem der Kanalfrequenzgang $H_{\rm K}(f)$ günstige Eigenschaften aufweist.

Darstellung der Amplitudenmodulation im Frequenzbereich

Die Grafik verdeutlicht die Aufgabenstellung, wobei folgende vereinfachende Annahmen getroffen sind:

Das gezeichnete Spektrum $Q(f)$ ist hier schematisch zu verstehen. Es besagt, dass in $q(t)$ nur Spektralanteile im Bereich $|f| ≤ B_{\rm NF}$ enthalten sind. $Q(f)$ könnte auch ein Linienspektrum sein.
Der Kanal sei in einem Bereich der Bandbreite $B_{\rm K}$ um die Frequenz $f_{\rm M}$ ideal, das heißt, es gelte $H_{\rm K}(f) =$ 1 für $|f – f_{\rm M}| ≤ B_{\rm K}/2.$ Rauschstörungen werden vorerst nicht betrachtet.
Das Trägersignal sei cosinusförmig (Phase $ϕ_T =$ 0) und besitze die Amplitude $A_{\rm T} =$ 1 (ohne Einheit). Die Trägerfrequenz $f_{\rm T}$ sei gleich der Mittenfrequenz des Übertragungsbandes.
Das Spektrum des Trägersignals $z(t) = \cos(ω_{\rm T} · t)$ lautet somit (in der Grafik grün eingezeichnet):

$Z(f) = \frac{1}{2} \cdot \delta (f + f_{\rm T})+\frac{1}{2} \cdot \delta (f - f_{\rm T})\hspace{0.05cm}.$

Beschreibung im Frequenzbereich (2)

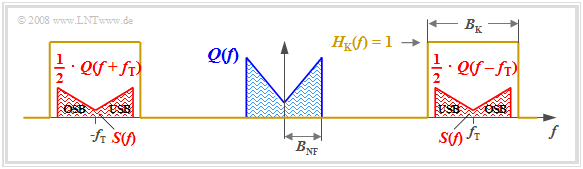
Wer mit den Gesetzmäßigkeiten der Spektraltransformation und insbesondere mit dem Faltungssatz vertraut ist, kann sofort eine Lösung für das Spektrum $S(f)$ des Modulatorausgangssignals angeben: $\begin{align*} S(f) & = Z(f) \star Q(f) = \frac{1}{2} \cdot \delta (f + f_{\rm T})\star Q(f)+\frac{1}{2} \cdot \delta (f - f_{\rm T})\star Q(f)\\ & = \frac{1}{2} \cdot Q (f + f_{\rm T})+\frac{1}{2} \cdot Q(f - f_{\rm T}) \hspace{0.05cm}.\end{align*}$

Bei dieser Gleichung ist berücksichtigt, dass die Faltung einer verschobenen Diracfunktion $δ(x – x_0)$ mit einer beliebigen Funktion $f(x)$ die verschobene Funktion $f(x – x_0)$ ergibt.

Die Grafik zeigt das Ergebnis. Man erkennt folgende Charakteristika:

Aufgrund der systemtheoretischen Betrachtungsweise mit positiven und negativen Frequenzen setzt sich $S(f)$ aus zwei Anteilen um $\pm f_{\rm T}$ zusammen, die jeweils formgleich mit $Q(f)$ sind.
Der Faktor 1/2 ergibt sich wegen der Trägeramplitude $A_{\rm T} =$ 1. Somit ist $s(t = 0)$ gleich $q(t = 0)$ , so dass auch die Integrale über deren Spektralfunktionen $S(f)$ bzw. $Q(f)$ gleich sein müssen.
Die Kanalbandbreite $B_{\rm K}$ muss mindestens doppelt so groß sein wie die Signalbandbreite $B_{\rm NF}$ , was zu der Namensgebung Zweiseitenband–Amplitudenmodulation (ZSB–AM) geführt hat.
Zu beachten ist, dass $B_{\rm NF}$ und $B_K$ absolute und nicht etwa äquivalente Bandbreiten sind. Letztere sind über flächengleiche Rechtecke definiert und werden im Tutorial mit $Δf_q$ bzw. $Δf_{\rm K}$ bezeichnet.
Die Spektralfunktion $S(f)$ beinhaltet keine Diraclinien bei der Trägerfrequenz $(\pm f_{\rm T})$ . Deshalb wird das hier beschriebene Verfahren auch als ZSB–AM ohne Träger bezeichnet.
Die Frequenzanteile oberhalb der Trägerfrequenz $f_{\rm T}$ nennt man das obere Seitenband (OSB), diejenigen unterhalb von $f_{\rm T}$ bezeichnet man als das untere Seitenband (USB).