Qualitätskriterien

1. Modulationsverfahren
2. Allgemeine Beschreibung
3. Qualitätskriterien

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Ideales und verzerrungsfreies System

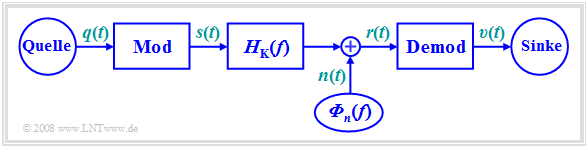
In allen nachfolgenden Kapiteln wird stets von folgendem Modell ausgegangen:

Die Aufgabe eines jeden Nachrichtenübertragungssystems besteht darin, an der räumlich entfernten Sinke ein Signal $υ(t)$ zur Verfügung zu stellen, das sich möglichst wenig vom Quellensignal $q(t)$ unterscheidet. Bei $υ(t) = q(t)$ würde man von einem idealen System sprechen.

In der Praxis werden sich die Signale $q(t)$ und $υ(t)$ stets unterscheiden, wofür es folgende Gründe gibt:

• Nichtideale Realisierung von Modulator und Demodulator,
• lineare Dämpfungs– und Phasenverzerrungen sowie Nichtlinearitäten,
• externe Störungen und stochastische Rauschprozesse,
• frequenzunabhängige Dämpfung und Laufzeit.

Ist nur die letztgenannte Einschränkung wirksam, so liegt ein verzerrungs– und rauschfreies System vor, und es gilt: $$v(t) = \alpha \cdot q(t- \tau).$$

Durch den Dämpfungsfaktor $α$ ist das Sinkensignal $υ(t)$ gegenüber dem Quellensignal $q(t)$ nur „leiser”. Auch eine Laufzeit $τ$ ist oft tolerabel, zumindest bei einer unidirektionalen Übertragung. Dagegen wird bei einer bidirektionalen Kommunikation – zum Beispiel einem Telefonat – schon eine Laufzeit von 300 Millisekunden als sehr störend empfunden.

Signal–zu–Stör–Leistungsverhältnis (1)

Im allgemeinen Fall wird sich das Sinkensignal $υ(t)$ auch gegenüber $α · q(t – τ)$ unterscheiden, und es gilt für das Fehlersignal: $$\varepsilon (t) = v(t) - \alpha \cdot q(t- \tau) = \varepsilon_{\rm V} (t) + \varepsilon_{\rm St} (t).$$

Dieses setzt sich aus zwei Anteilen zusammen:

• den linearen und nichtlinearen Verzerrungen $ε_{\rm V}(t)$, die durch Modulator, Kanal und Demodulator hervorgerufen werden können und deterministisches Verhalten zeigen,
• der stochastischen Komponente $ε_{\rm St}(t)$, die von der HF–Störung $n(t)$ am Demodulatoreingang herrührt. Im Gegensatz zu $n(t)$ handelt es sich bei $ε_{\rm St}(t)$ um eine niederfrequente Störung.

Als Maß für die Qualität des Nachrichtensystems wird das Signal–zu–Stör–Leistungsverhältnis $ρ_υ$ an der Sinke als Quotient der Leistungen (Varianzen) von Nutzanteil $υ(t) – ε(t)$ und Störanteil $ε(t)$ definiert: $$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}} {[v(t)-\varepsilon(t)]^2 }\hspace{0.1cm}{\rm d}t,$$ $$P_{\varepsilon} = \overline{\varepsilon^2(t)} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t$$ $$\Rightarrow \hspace{0.5cm}\rho_{v} = \frac{ P_{v -\varepsilon}}{P_{\varepsilon}} \hspace{0.05cm}.$$

Für die Leistung des Nutzanteils erhält man unabhängig von der Laufzeit $τ$: $$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \overline{\alpha^2 \cdot q^2(t - \tau)}= \alpha^2 \cdot P_{q}.$$ Hierbei bezeichnet $P_q$ die Leistung des Quellensignals $q(t)$: $$P_{q} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}} {q^2(t) }\hspace{0.1cm}{\rm d}t .$$ Damit erhält man: $$\rho_{v} = \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{v} = 10 \cdot {\rm lg} \hspace{0.15cm} \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon}} \hspace{0.05cm}.$$ Im Folgenden bezeichnen wir $ρ_υ$ kurz als das Sinken–SNR (Signal–to–Noise–Ratio) und 10 · lg $ρ_υ$ als den Sinken–Störabstand, der bei Verwendung des Zehner–Logarithmus (lg) in dB angegeben wird.