Das Gram-Schmidt-Verfahren
Inhaltsverzeichnis
Programmbeschreibung
Das Applet verdeutlicht das »Gram–Schmidt–Verfahren«. Dieses ermöglicht, eine Menge {s1(t),...,sM(t)} energiebegrenzter Signale mit Hilfe von N≤M orthonormalen Basisfunktionen φ1(t),...,φN(t) in folgender Form darzustellen:
- si(t)=N∑j=1sij⋅φj(t),i=1,...,M,j=1,...,N.
Der vektorielle Repräsentant der Musterfunktion s1(t) lautet dann:
- si=(si1,si2,...,siN).
Das Applet zeigt alle Grafiken, die zum Verständnis des Gram–Schmidt–Verfahrens erforderlich sind, und als jeweiliges Ergebnis
- die 2D–Darstellung der M vektoriellen Repräsentanten, falls N=2,
- die 3D–Darstellung der M vektoriellen Repräsentanten, falls N=3.
English Description
This applet illustrates the »Gram–Schmidt process«. This allows to represent a set {s1(t),...,sM(t)} of energy-limited signals in the following form, using N≤M orthonormal basis functions φ1(t),...,φN(t):
- si(t)=N∑j=1sij⋅φj(t),i=1,...,M,j=1,...,N.
The vectorial representative of the pattern function s1(t) is then:
- si=(si1,si2,...,siN).
The applet shows all the graphics, necessary to understand the Gram–Schmidt process, and as the respective result.
- the two-dimensional representation of the M vectorial representatives, if N=2,
- the three-dimensional representation of the M vectorial representatives, if N=3.
Theoretischer Hintergrund
Signaldarstellung mit orthonormalen Basisfunktionen
Wir gehen von einer Menge {si(t)} möglicher Sendesignale aus, die den möglichen Nachrichten mi eineindeutig zugeordnet sind. Mit i=1, ... , M gelte:
- m∈{mi},s(t)∈{si(t)}:m=mi⇔s(t)=si(t).
Für das Folgende setzen wir weiter voraus, dass die M Signale si(t) energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.
Satz: Eine jede Menge {s1(t),...,sM(t)} energiebegrenzter Signale lässt sich in N≤M orthonormale Basisfunktionen φ1(t),...,φN(t) entwickeln. Es gilt:
- si(t)=N∑j=1sij⋅φj(t),i=1,...,M,j=1,...,N.
Jeweils zwei Basisfunktionen φj(t) und φk(t) müssen orthonormal zueinander sein, das heißt, dass gelten muss (δjk nennt man das Kronecker–Symbol):
- <φj(t),φk(t)>=∫+∞−∞φj(t)⋅φk(t)dt=δjk={10fallsj=kfallsj≠k.
Der Parameter N gibt dabei an, wieviele Basisfunktionen φj(t) benötigt werden, um die M möglichen Sendesignale darzustellen. Mit anderen Worten: N ist die »Dimension des Vektorraums«, der von den M Signalen aufgespannt wird. Dabei gilt:
- Ist N=M, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien Ei= <si(t),si(t)> können durchaus ungleich Eins sein.
- Der Fall N<M ergibt sich, wenn mindestens ein Signal si(t) als Linearkombination von Basisfunktionen φj(t) dargestellt werden kann, die sich bereits aus anderen Signalen sj(t)≠si(t) ergeben haben.
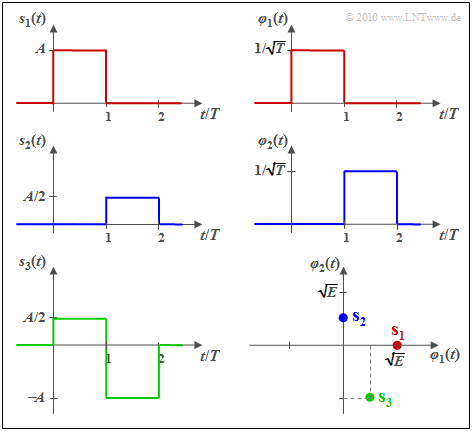
Beispiel 1: Wir betrachten M=3 energiebegrenzte Signale gemäß der Grafik.
Man erkennt sofort:
- Die Signale s1(t) und s2(t) sind zueinander orthogonal.
- Die Energien sind E1=A2⋅T=E und E2=(A/2)2⋅T=E/4.
- Die Basisfunktionen φ1(t) und φ2(t) sind jeweils formgleich mit s1(t) bzw. s2(t).
- Beide Signale besitzen jeweils die Energie „Eins”:
- φ1(t)=s1(t)√E1=s1(t)√A2⋅T=1√T⋅s1(t)A
- ⇒s1(t)=s11⋅φ1(t),s11=√E,
- φ2(t)=s2(t)√E2=s2(t)√(A/2)2⋅T=1√T⋅s2(t)A/2
- ⇒s2(t)=s21⋅φ2(t),s21=√E/2.
- Das Signal s3(t) kann durch die vorher bestimmten Basisfunktionen φ1(t) und φ2(t) ausgedrückt werden:
- s3(t)=s31⋅φ1(t)+s32⋅φ2(t),
- ⇒s31=A/2⋅√T=√E/2,s32=−A⋅√T=−√E.
Trotz M=3 gilt also im vorliegenen Fall nur N=2.
Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen φ1(t) und φ2(t) als Achsen dargestellt, wobei E=A2⋅T gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist.
Die vektoriellen Repräsentanten der Signale s1(t), s2(t) und s3(t) in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:
- s1=(√E,0),s2=(0,√E/2),s3=(√E/2,−√E).
Das Verfahren nach Gram-Schmidt
Im letzten Beispiel war die Bestimmung der beiden orthonormalen Basisfunktionen φ1(t) und φ2(t) sehr einfach, da diese formgleich mit s1(t) bzw. s2(t) waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen φ1(t), ... , φN(t) für beliebig vorgebbare Signale s1(t), ... , sM(t), und zwar wie folgt:
- Die erste Basisfunktion φ1(t) ist stets formgleich mit s1(t). Es gilt:
- φ1(t)=s1(t)√E1=s1(t)||s1(t)||⇒||φ1(t)||=1,s11=||s1(t)||,s1j=0f¨urj≥2.
Hinweise zur Nomenklatur:
(1) Ausgehend von zwei reellen und energiebegrenzten Zeitfunktionen x(t) und y(t) erhält man für das innere Produkt allgemein:
- <x(t),y(t)>=∫+∞−∞x(t)⋅y(t)dt.
(2) Daraus ergibt sich die Euklidische Norm der Zeitfunktion s1(t):
- ||s1(t)||=√<s1(t),s1(t)>
Es wird nun angenommen, dass aus den Signalen s1(t), ... , sk−1(t) bereits die Basisfunktionen φ1(t), ... , φn−1(t) berechnet wurden (n≤k).
- Dann berechnen wir mittels der nächsten Funktion sk(t) die Hilfsfunktion
- θk(t)=sk(t)−n−1∑j=1skj⋅φj(t)mitskj=<sk(t),φj(t)>,j=1,...,n−1.
- Hat diese Hilfsfunktion die Norm ||θk(t)||=0, so liefert sk(t) keine neue Basisfunktion. Vielmehr lässt sich dann sk(t) durch die n−1 bereits vorher gefundenen Basisfunktionen φ1(t), ... , φn−1(t) ausdrücken:
- sk(t)=n−1∑j=1skj⋅φj(t).
- Eine neue Basisfunktion (nämlich die n–te) ergibt sich nur für den Fall ||θk(t)||≠0:
- φn(t)=θk(t)||θk(t)||⇒||φn(t)||=1.
Diese Prozedur wird solange fortgesetzt, bis alle M Signale berücksichtigt wurden.
- Danach hat man alle N≤M orthonormalen Basisfunktionen φj(t) gefunden.
- Der Sonderfall N=M ergibt sich nur dann, wenn alle M Signale linear voneinander unabhängig sind.
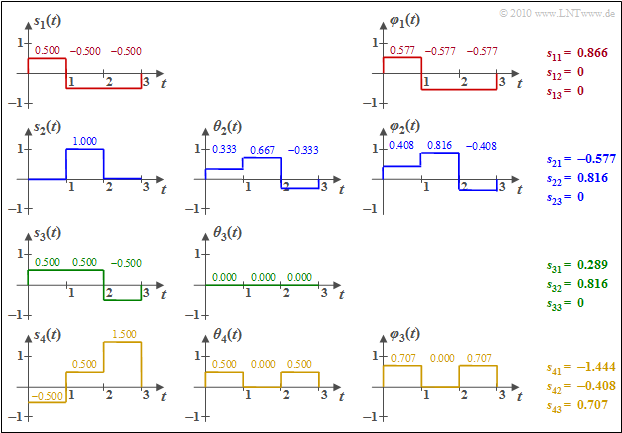
Beispiel 2: Wir betrachten die M=4 energiebegrenzten Signale s1(t), ... , s4(t) entsprechend der Grafik. Zur Vereinfachung der Berechnungen sind hier sowohl die Amplituden als auch die Zeit normiert.
Man erkennt aus diesen Skizzen:
- Die Basisfunktion φ1(t) ist formgleich mit s1(t). Wegen E1=||s1(t)||2=3⋅0.52=0.75 ergibt sich s11=||s1(t)||=0.866. φ1(t) selbst besitzt abschnittsweise die Werte ±0.5/0.866=±0.577.
- Zur Berechnung der Hilfsfunktion θ2(t) berechnen wir
- s21=<s2(t),φ1(t)>=0⋅(+0.577)+1⋅(−0.577)+0⋅(−0.577)=−0.577
- ⇒θ2(t)=s2(t)−s21⋅φ1(t)=(0.333,0.667,−0.333)⇒||θ2(t)||2=(1/3)2+(2/3)2+(−1/3)2=0.667
- ⇒s22=√0.667=0.816,φ2(t)=θ2(t)/s22=(0.408,0.816,−0.408).
- Die inneren Produkte zwischen s1(t) mit φ1(t) bzw. φ2(t) liefern folgende Ergebnisse:
- s31=<s3(t),φ1(t)>=0.5⋅(+0.577)+0.5⋅(−0.577)−0.5⋅(−0.577)=0.289,
- s32=<s3(t),φ2(t)>=0.5⋅(+0.408)+0.5⋅(+0.816)−0.5⋅(−0.408)=0.816
- ⇒θ3(t)=s3(t)−0.289⋅φ1(t)−0.816⋅φ2(t)=0.
Das bedeutet: Die grüne Funktion s3(t) liefert keine neue Basisfunktion φ3(t), im Gegensatz zur Funktion s4(t). Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.
Die verschiedenen Rubriken bei der Auswahl der Programmparameter
Das Programm bietet insgesamt 4⋅6=24 Möglichkeiten zur Einstellung der jeweiligen Menge {si(t)} möglicher Sendesignale. Diese 24 Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt:
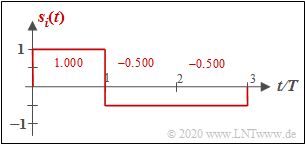
(1) Rubrik »Basisband« ⇒ gültig für die Einstellungen (A) ... (F):
- Jedes Mustersignal si(t) besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer T.
- Die einzelnen Rechteckhöhen sind Vielfache von ±0.25 und die gesamte Signaldauer ergibt 3T.
- Mit dem seitlichen Slider kann man das Signal si(t) um Vielfache von ±0.25 nach oben und unten verschieben.
- Solche Signale treten zum Beispiel bei der binären oder mehrstufigen Basisbandübertragung auf.
- Im Beispiel 2 des hier angegebenen Links erkennt man zum Beispiel die grafischen Darstellungen
- eines binären Signals q(t),
- eines ternären Signals s3(t),
- eines quaternären Signals s4(t).
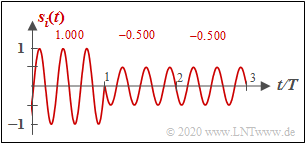
(2) Rubrik »M-ASK/BPSK« ⇒ gültig für die Einstellungen (G) ... (L):
- Die Mustersignale si(t) haben ebenfalls die Dauer 3T und sind ähnlich aufgebaut wie bei der Rubrik (1).
- Im Unterschied zu (1) wird jede Rechteckfunktion (Dauer T) durch eine Periode einer Sinusfunktionen ersetzt.
- Der angegebene Zahlenwert gibt hier die Amplitude des sinusförmigen Teilstücks an.
- Bei negativem Vorzeichen wird aus dem „Sinus” die Funktion „Minus–Sinus”.
- Mit dem seitlichen Slider kann man die Amplitude von si(t) um Vielfache von ±0.25 vergrößern oder verkleinern.
- Solche Signale können zum Beispiel bei der M–ASK (mehrstufiges "Amplitude Shift Keying") auftreten, ebenso bei BPSK ("Binary Phase Shift Keying").
(3) Rubrik »Nur eine Frequenz« ⇒ gültig für die Einstellungen (M) ... (R):
- Alle Mustersignale si(t) haben die Dauer T und sind jeweils Harmonische Schwingungen der Form
- si(t)=Ai⋅cos(2π⋅fk⋅t+ϕi)mitfk=K/T.
- Die Eigenschaft „Nur eine Frequenz” bezieht sich auf die einzelnen Mustersignale si(t) und auf den gesamten Set.
- Der Parameter K gibt die Anzahl der Schwingungen innerhalb der Zeit T an und gilt für alle Mustersignale.
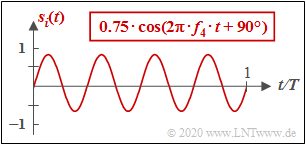
- Die Grafik gilt für: Ai=0.75,fk=4/T⇒K=4,ϕi=−90∘ ⇒ sinusförmiger Verlauf.
- Mit dem Slider lässt sich die Phase von si(t) um Vielfache von ±22.5∘ in beide Richtungen variieren.
- Solche Harmonische haben für alle (analogen und digitalen) Nachrichtensysteme große Bedeutung.
(4) Rubrik »Mehrere Frequenzen« ⇒ gültig für die Einstellungen (S) ... (X):
- Es gelten ähnliche Voraussetzungen wie für die „Rubrik 3”, es sind aber nun stets mehrere Frequenzen beteiligt.
- Die Eigenschaft „Mehrere Frequenzen” bezieht sich auf einzelne Mustersignale si(t) oder auch auf den gesamten Set {si(t)}.
- Möglich sind somit auch Mustersignale der folgenden Form (mit k=0 ⇒ f=f0=k/T=0 ⇒ Gleichsignal):
- si(t)=1⋅cos(2π⋅f0⋅t)−0.5⋅cos(2π⋅f2⋅t)−0.5⋅cos(2π⋅f3⋅t).
- Der Parameter k muss auch nicht ganzzahlig sein. Beispielsweise kennzeichnet k=4.5 viereinhalb Schwingunen Schwingungen innerhalb der Zeitdauer T.
- Mit dem Slider können die Frequenzkenngrößen k um Vielfache von 0.25 vergrößert oder verkleinert werden.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Es gilt die Einstellung A. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”.
- Einstellung A beschreibt das Beispiel 2 im Theorieteil. Die Basisfunktion φ1(t) ist identisch mit dem Signal s1(t), aber mit Signalenergie E=1.
- Es gibt hier nur N=3 Basisfunktionen, da die Hilfsfunktion θ3(t) identisch Null ist.
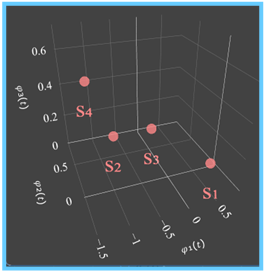
- Die vektoriellen Repräsentanten der Signale s1(t), ... , s4(t) können im 3D–Vektorraum abgelesen werden; Beispiel: s4=(−1.444,−0.408,+0.707).
(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung B. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.
- Auch hier gibt es N=3 Basisfunktionen. Bei Änderung auf s4=(−1,−1,0) nur mehr N=2.
(3) Bei der Einstellung C ist die Reihenfolge der Signale gegenüber B vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?
- Auch hier gibt es N=3 Basisfunktionen, aber nun andere: Nämlich φ1(t)=s1(t), φ2(t)=s2(t), φ3(t)=s3(t).
(4) Die M=4 Signale der Einstellung D lassen sich durch nur N=2 Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.
- Es gilt s3(t)=s1(t)/4−s2(t)/2 und s4(t)=−s1(t)−s2(t). Das heißt: s3(t) und s4(t) liefern keine neuen Basisfunktionen.
(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung E im Vergleich zur Einstellung D.
- Bei der Einstellung E ist die Reihenfolge der Signale gegenüber der Einstellung D vertauscht. Ähnlich wie zwischen B und C.
- Auch diese M=4 Signale lassen sich somit durch nur N=2 Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).
(6) Welches Ergebnis liefern die vier Signale gemäß der Einstellung F?
- Die die Signale s1(t), ... , s4(t) basieren alle auf einer einzigen Basisfunktion φ1(t), die formgleich mit s1(t) ist. Es gilt N=1.
- Die vektoriellen Repräsentanten der Signale s1(t), ... , s4(t) sind ±0.866 und ±1.732. Sie liegen inder 2D–Darstellung alle auf einer Linie.
(7) Es gilt nun die „M–ASK / BPSK”–Einstellung G. Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung A.
- Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor √2 aus.
- Somit ist nun der vektorielle Repräsentant des unteren Signals s4=(−1.021,−0.289,+0.500) anstelle von s4=(−1.444,−0.408,+0.707).
- Bei der Einstellung H sind gegenüber G alle Amplituden verdoppelt. Somit ergibt sich hier s4=(−2.041,−0.577,+1.000).
(8) Es gelte die „M–ASK / BPSK”–Einstellung I. Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung C, aber nun mit nur halb so großen Energien.
- Somit ist nun der vektorielle Repräsentant des unteren Signals s4=(+0.707,−0.707,0.000) anstelle von s4=(+1.000,−1.000,0.000).
- Somit ist nun der vektorielle Repräsentant des unteren Signals s4=(+0.707,−0.707,0.000) anstelle von s4=(+1.000,−1.000,0.000).
- Mit der „M–ASK / BPSK”–Einstellung J wird eine ähnliche Konstellation betrachtet wie mit der „Basisband”–Einstellung D. Gleiches gilt für K und E.
(9) Es gelte die „M–ASK / BPSK”–Einstellung L. Interpretieren Sie das Ergebnis. Gibt es einen Zusammenhang zu einer früheren Aufgabe?
- Die Einstellung L ist vergleichbar mit der obigen Einstellung F. Es gilt N=1. Das heißt:
- Alle M=4 Signale sind allein durch die Basisfunktion φ1(t) darstellbar, die formgleich mit s1(t) ist.
(10) Nun gelte die „Nur eine Frequenz”–Einstellung M. Interpretieren Sie die dargestellten Grafiken.
- Alle Signale si(t) haben die Amplitude Ai=1 und gleiche Frequenz f=f1. Das heißt: Jeweils eine Schwingung innerhalb der Zeit T.
- Die M=4 Signale unterscheiden sich nur durch die Phasen ϕ1=+45∘, ϕ2=+135∘, ϕ3=−135∘ und ϕ4=−45∘. Es gibt N=2 Basisfunktionen.
- Die Basisfunktion φ1(t) ist formgleich mit s1(t) und φ2(t) ist formgleich mit s2(t). Dies gilt für die meisten Einstellungen der dritten Rubrik.
- Die vektoriellen Repräsentanten der Signale lauten: s1=(0.707,0), s2=(0,0.707), s3=(−0.707,0), s4=(0,−0.707).
(11) Welche Unterschiede gibt es mit der Einstellung N gegenüber der Einstellung M?
- Die vier Mustersignale si(t) beschreiben nun von oben nach unten einen Cosinus, einen Sinus, einen Minus–Cosinus und einen Minus–Sinus.
- Für die N=2 Basisfunktionen gilt: φ1(t)=√2⋅cos(2πf1t), φ2(t)=√2⋅sin(2πf1t). Auch s3(t) und s4(t) lassen sich damit beschreiben.
- Die vektoriellen Repräsentanten der Signale lauten: s1=(0.707,0), s2=(0,0.707), s3=(−0.354,0), s4=(0,−0.354).
- Dieses Ergebnis berücksichtigt die nur halb so großen Amplituden von s3(t) und s4(t) gegenüber s1(t) und s2(t).
(12) Wie unterscheidet sich die Einstellung O von der Einstellung N? Analysieren Sie den vektoriellen Repräsentanten für s3 genauer.
- Das Signal s2(t) bei Einstellung O ist minus–sinusförmig ⇒ φ1(t)=√2⋅cos(2πf1t), φ2(t)=−√2⋅sin(2πf1t).
- Für die Darstellung Harmonischer Schwingungen werden häufig diese Basisfunktionen „Cosinus” und „Minus–Sinus” verwendet.
- Außerdem unterscheiden sich die Signale s3(t) und s4(t) durch die halbe Amplitude und die Phsenwerte sind keine Vielfachen von 90∘.
- Die vektoriellen Repräsentanten der Signale lauten: s1=(0.707,0), s2=(0,0.707), s3=(0.612,0.354), s4=(0.354,−0.612). Überprüfung:
- s3(t)=cos(2πf1t+30∘)=cos(30∘)⋅cos(2πf1t)−sin(30∘)⋅sin(2πf1t)=√3/(2√2)⋅φ1(t)+1/(2√2)⋅φ2(t)=0.612⋅φ1(t)+0.354⋅φ2(t).
(13) Wie unterscheidet sich die Einstellung P von der Einstellung O? Gibt es in der Rubrik „Nur eine Frequenz” eine Einstellung für N=1 ?
- Mit der Einstellung P ergeben sich gleiche vektorielle Repräsentanten. Einziger Unterschied zur Einstellung O ist die doppelte Frequenz.
- Das Ergebnis N=1 ist nur möglich, wenn alle Signale gleiche Frequenz und gleiche Phase besitzen ⇒ Einstellung R (unterschiedliche Amplituden).
(14) Nun gelte die „Mehrere Frequenzen”–Einstellung S. Interpretieren Sie die dargestellten Grafiken.
- Die vier Signale s1(t) ... s4(t) weisen nun unterschiedliche Frequenzen auf: f=0 (Gleichsignal), f=f1, f=f2=2f1, f=f3=3f1.
- Deshalb ergeben sich hier N=4 Basisfunktionen φi(t), die alle formgleich mit den entsprechenden Signalen si(t) sind. Für i=1 gilt: φ1(t)=1.
- Die weiteren Basisfunktionen haben wegen der Energienormierung einheitlich die Form φi(t)=√2⋅cos(2πfit).
(15) Wie unterscheidet sich die Einstellung T von der Einstellung S? Begründen Sie das Ergebnis N=3. Interpretieren Sie auch die Grafiken zur Einstellung U.
- Die Signale s1(t) ... s3(t) beinhalten die Frequenzen f=0, f=f1 und f=f2=2f1. Jedes Signal erzwingt eine eigene Basisfunktion.
- Die vektoriellen Repräsentanten dieser Signale lauten: s1=(1,0,0), s2=(0,0.707,0), s3=(0,0,0.707).
- Das vierte Signal ist als Linearkombination darstellbar: s4(t)=s1(t)−0.5⋅s2(t)−0.5⋅s3(t) ⇒ vektorieller Repräsentant: s1=(1,−0.354,0.354).
- Die Einstellung U ist nur eine zyklische Vertauschung von der Einstellung T ⇒ es genügen ebenfalls N=3 Basisfunktionen.
- Die N=3 Basisfunktionen sind aber deutlich komplizierter als bei T, weil „Gram–Schmidt” signifikant von der Reihenfolge der Mustersignale abhängt.
(16) Interpretieren Sie die dargestellten Grafiken für die Einstellung V und anschließend für die Einstellung W.
- Die ersten drei Signale führen zu je einer cosinusförmigen Basisfunktion mit den Frequenzen f2, f3 und f4.
- Das letzte Signal ist s4(t)=cos(2πf3t)⋅cos(2πf1t)=1/2⋅[cos(2π⋅(f3−f1)⋅t)+cos(2π⋅(f3+f1)⋅t)]=1/2⋅[cos(2πf2t)+cos(2πf4t)].
- Der vektorielle Repräsentant des untersten Signals gemäß Einstellung V lautet somit: s4=(0.354,0,0.354).
- Bei der Einstellung W ergeben sich genau die gleichen Basisfunktionen wie bei W. Hier erhält man für das unterste Signal s4=(0.354,0,−0.354).
- Begründung s4(t)=sin(2πf3t)⋅sin(2πf1t)=1/2⋅[cos(2πf2t)−cos(2πf4t)]. Auch hier liefert die Basisfunktion φ2(t) keinen Beitrag.
(17) Wie viele Basisfunktionen benötigt man für die vier Signale gemäß der Einstellung X?
- Das Ergebnis lautet: N=4. Jedes der vier Signale cos(2πf1t), sin(2πf1t) cos(2πf2t), sin(2πf2t) führt zu einer neuen Basisfunktion.
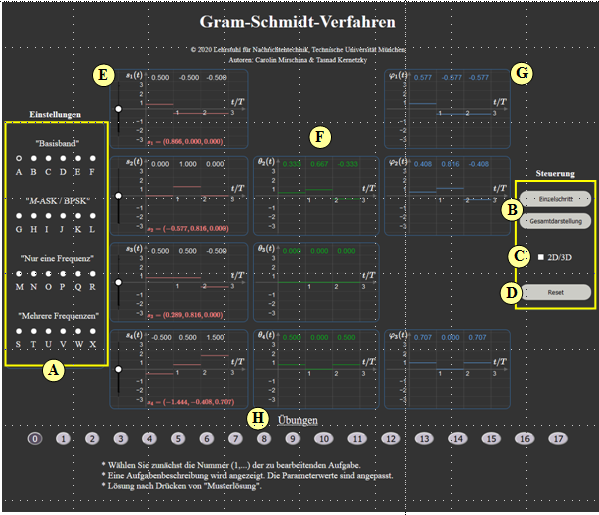
Zur Handhabung des Applets
(A) Auswahl zwischen 24 Parametersätze für {s1(t),...,sM(t)}
(B) Umschaltung: Einzelschritt / Gesamtdarstellung
(C) 2D– bzw. 3D–Darstellung der vektoriellen Repräsentanten
(siehe rechte Grafik, Koordinatensystem kann gedreht werden)
(D) Reset – Rücksetzung aller Parameter auf Grundeinstellung
(E) Grafikfeld zur Darstellung der Mustersignale sk(t)
(F) Grafikfeld zur Darstellung der Hilfsfunktionen θk(t)
(G) Grafikfeld zur Darstellung der Basisfunktionen φk(t)
(H) Bereich für die Versuchsdurchführung: Aufgabenauswahl
Über die Autoren
Dieses interaktive Berechnungstool wurde am »Lehrstuhl für Nachrichtentechnik« der »Technischen Universität München« konzipiert und realisiert.
- Die erste Version wurde 2008 von »Martin Völkl« im Rahmen seiner Diplomarbeit mit »FlashMX–Actionscript« erstellt (Betreuer: »Günter Söder«).
- 2020 wurde das Programm von »Carolin Mirschina« im Rahmen einer Werkstudententätigkeit mit „HTML5” neu gestaltet (Betreuer: »Tasnád Kernetzky«).
Die Umsetzung dieses Applets auf HTML 5 wurde durch das Programm »EXIni« (Exzellenzinitiative) der Technischen Universität München gefördert. Wir bedanken uns.