Allgemeine Beschreibung linearer Blockcodes

1. Kanalcodierung
2. Binäre Blockcodes zur Kanalcodierung
3. Allgemeine Beschreibung linearer Blockcodes

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Lineare Codes und zyklische Codes

Alle bisher behandelten Codes,

• der  "Single Parity–check Code",
• der  "Repetition Code"  und
• der  Hamming–Code

sind linear. Nun wird die für binäre Blockcodes gültige Definition von Linearität nachgereicht.

$\text{Definition:}$  Ein  linearer binärer Blockcode  $\mathcal{C}$ ist ein Satz von  $2^k$  Codeworten  $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$, wobei die (Modulo–2)–Summe zweier beliebiger Codeworte  $\underline{x}$  und  $\underline{x}\hspace{0.05cm}'$  wiederum ein gültiges Codewort ergibt:

$$\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x} + \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.05cm}.$$

Diese Bedingung muss auch für  $\underline{x} = \underline{x}\hspace{0.05cm}'$  erfüllt sein.

Hinweis:   Die Modulo–Addition wird für den Rest dieses Buches zur Vereinfachung der Schreibweise nicht mehr durch das Modulo–Additionszeichen ausgedrückt, sondern mit dem herkömmlichen Pluszeichen.

$\text{Beispiel 1:}$  Wir betrachten zwei  $\text{(3, 2)}$–Blockcodes:

$$\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},$$

$$\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.$$

Man erkennt:

• Der Code  $\mathcal{C}_1$  ist linear, da die Modulo–2–Addition zweier beliebiger Codeworte stets auch ein gültiges Codewort ergibt, z.B.  $(0, 1, 1) + (1, 0, 1) = (1, 1, 0)$.
  

• Die obige Definition gilt auch für die Modulo–2–Addition eines Codewortes mit sich selbst, zum Beispiel  $(0, 1, 1) + (0, 1, 1) = (0, 0, 0)$
    ⇒   Jeder lineare Code beinhaltet das Nullwort  $\underline{0}$.
  

• Obwohl die letzte Voraussetzung erfüllt wird, ist  $\mathcal{C}_2$  kein linearer Code. Für diesen Code gilt nämlich beispielsweise:   $(0, 1, 1) + (1, 1, 0) = (1, 0, 1)$. Dies ist kein gültiges Codewort von  $\mathcal{C}_2$.

Im Folgenden beschränken wir uns ausschließlich auf lineare Codes, da nichtlineare Codes für die Praxis von untergeordneter Bedeutung sind.

$\text{Definition:}$  Ein linearer Blockcode  $\mathcal{C}$  heißt  zyklisch, wenn jede zyklische Verschiebung eines Codewortes  $\underline{x}$  (nach links oder rechts) ein gültiges Codewort ergibt:

$$\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, \hspace{0.05cm}\text{...} \hspace{0.05cm} \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} \hspace{0.05cm}.$$

Codetabelle des systematischen  $\text{(7, 4, 3)}$–Hamming–Codes;
schwarz:   $k= 4$  Informationsbits, rot:   $n-k = 3$  Prüfbits

$\text{Beispiel 2:}$ 

• Man erkennt aus der Tabelle für den  $\text{HC (7, 4, 3)}$, dass dieser linear und zyklisch ist.
• Es ergibt sich auch dann ein gültiges Codewort, wenn man alle Bit invertiert:   $0 ↔ 1$.
• Auch das  $\underline{0}$–Wort  ($n$  mal eine „Null”) und das  $\underline{1}$–Wort ($n$  mal eine „Eins”) sind bei diesem Code zulässig.

Codefestlegung durch die Prüfmatrix

$\text{(7, 4, 3)}$–Hamming–Code

Wir betrachten den  $\text{(7, 4, 3)}$–Hamming–Code  mit Codeworten  $\underline{x}$  der Länge  $n=7$, bestehend aus

• $k = 4$  Informationsbits  $x_1$,  $x_2$,  $x_3$,  $x_4$, und
  
• $m = n-k = 3$  Prüfbits $x_5$,  $x_6$,  $x_7$.
  
  

Die Paritätsgleichungen lauten somit:

$$x_1 + x_2 + x_3 + x_5 = 0 \hspace{0.05cm},$$

$$x_2 + x_3 + x_4 + x_6 = 0 \hspace{0.05cm},$$

$$x_1 + x_2 + x_4 + x_7 = 0 \hspace{0.05cm}.$$

In Matrixschreibweise lautet dieser Gleichungssatz:

$${ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}.$$

In dieser Gleichung werden verwendet:

• die  Prüfmatrix  ${ \boldsymbol{\rm H}}$  mit  $m = n-k = 3$  Zeilen und  $n = 7$  Spalten:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 & 0 & 0\\ 0 &1 &1 &1 &0 & 1 & 0\\ 1 &1 &0 &1 &0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},$$

• das  Codewort  $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_7)$  der Länge  $n = 7$,
  

• der  Nullvektor  $\underline{0} = (0, 0, 0)$  der Länge  $m = 3$.
  
  

Durch Transponieren werden aus den  Zeilenvektoren  $\underline{x}$  und  $\underline{0}$  die entsprechenden  Spaltenvektoren  $\underline{x}^{\rm T}$  und  $\underline{0}^{\rm T}$.

$\text{(6, 3, 3)}$–Blockcode

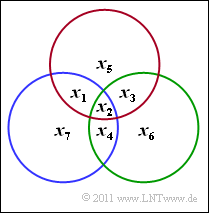
$\text{Beispiel 3:}$  Die Grafik illustriert die  $m = 3$  Paritätsgleichungen eines Codes  $\mathcal{C}$  mit den Codeparametern  $n = 6$  und  $k = 3$  in der Reihenfolge rot, grün und blau. Es handelt sich also nicht um einen Hamming–Code  $(n \ne 2^m-1)$.

Entsprechend der Gleichung  $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T}$  lautet die Prüfmatrix:

$$\boldsymbol{\rm H} = \begin{pmatrix} 1 &1 &0 &1 &0 & 0\\ 1 &0 &1 &0 &1 & 0\\ 0 &1 &1 &0 &0 & 1 \end{pmatrix}\hspace{0.05cm}.$$

Die  $2^k = 8$  Codeworte bei systematischer Realisierung lauten (mit den Prüfbits rechts vom kleinen Pfeil):

$$\underline{x}_0 = (0, 0, 0_{\hspace{0.01cm} \rightarrow} 0, 0, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_1 = (0, 0, 1_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_2 = (0, 1, 0_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm}\underline{x}_3 = (0, 1, 1_{\hspace{0.01cm} \rightarrow}1, 1, 0)\hspace{0.05cm},$$ $$\underline{x}_4 = (1, 0, 0_{\hspace{0.01cm} \rightarrow} 1, 1, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_5 = (1, 0, 1_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_6 = (1, 1, 0_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_7 = (1, 1, 1_{\hspace{0.01cm} \rightarrow}0, 0, 0)\hspace{0.05cm}.$$

Man erkennt aus diesen Angaben:

• Die Spaltenanzahl  $\boldsymbol{\rm H}$  ist gleich der Codelänge $n$.
  

• Die Zeilenanzahl von  $\boldsymbol{\rm H}$  ist gleich der Anzahl  $m = n-k$  der Prüfgleichungen.
  

• Aus  $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T}$  folgt also nicht, dass alle Codeworte eine gerade Anzahl von Einsen beinhalten.

Codefestlegung durch die Generatormatrix

Die Prüfmatrix  $\boldsymbol{\rm H}$  eines  $(n, k)$–Blockcodes hat  $m = n-k$  Zeilen und  $n$  Spalten. Den gleichen Code kann man aber auch durch die Matrix  $\boldsymbol{\rm G}$  mit ebenfalls  $n$  Spalten, aber  $k$  Zeilen beschreiben:

$\text{Definition:}$  Ein linearer binärer Blockcode  $\mathcal{C}$  kann durch die  Prüfmatrix  $\boldsymbol{\rm H}$  bzw. mit der  Generatormatrix  $\boldsymbol{\rm G}$  wie folgt charakterisiert werden:

$$\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\text{:} \hspace{0.2cm}{ \boldsymbol{\rm H} } \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},$$

$$\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{0.05cm}, \hspace{0.1cm}\underline{u} \in {\rm GF}(2^k)\text{:} \hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G} } \}\hspace{0.05cm}.$$

Bevor wir uns den Eigenschaften der Generatormatrix zuwenden, beschreiben wir an einem Beispiel die Erzeugung der Codeworte.

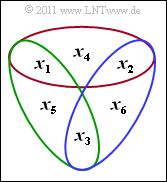
$\text{Beispiel 4:}$  Wir betrachten einen linearen  $(5, 3)$–Blockcode mit der Generatormatrix (auch dies ist kein Hamming–Code)

$$\boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix} \hspace{0.05cm}.$$

Damit werden die Informationsworte  $\underline{u}= (u_1, u_2, u_3)$  den Codeworten  $\underline{x}= (x_1, x_2, x_3, x_4, x_5)$  gemäß folgenden Gleichungen zugeordnet.
Es gilt stets  $\underline{x} = \underline{u} \cdot \boldsymbol{\rm G}$:

$$\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},$$

$$\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_1 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{g}_3\hspace{0.05cm},$$

$$\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_2 = (0, 1, 0, 1, 0)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2\hspace{0.05cm},$$

$$\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_3 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2+\underline{g}_3\hspace{0.05cm},$$

$$\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_4 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1 \hspace{0.05cm},$$

$$\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_3\hspace{0.05cm},$$

$$\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_6 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_2\hspace{0.05cm},$$

$$\underline{u}_7 =(1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.$$

Anmerkungen:

• Die hier zur Berechnung herangezogenen Basisvektoren  $\underline{g}_1$,  $\underline{g}_2$  und  $\underline{g}_3$  – jeweils mit der Länge  $n = 5$  – entsprechen den  $k = 3$  Zeilen der Generatormatrix  $\boldsymbol{\rm G}$.
• Dieser Code ist wegen  $d_{\rm min} = 1$  weder zur Fehlerkorrektur noch zur Fehlererkennung geeignet ist. Trotzdem wird dieser Code auch auf den nächsten Seiten beispielhaft betrachtet, weil die Codierergebnisse gut interpretierbar sind.
  
• Wir möchten Sie an dieser Stelle auf das Applet  Gram–Schmidt–Verfahren  zum Buch „Digitalsignalübertragung” aufmerksam machen, das die Berechnung von Basisfunktionen vermittelt, wenn auch in einem anderen als dem hier gebrauchten Zusammenhang.
  

Identische Codes

Die im  $\text{Beispiel 4}$  auf der letzten Seite verwendeten Vektoren  $\underline{g}_1$,  $\underline{g}_2$,  ...  ,  $\underline{g}_k$  sind die  Basisvektoren  des linearen Blockcodes  $\mathcal{C}$.

• Der Code selbst kann als  $k$–dimensionaler Untervektorraum von  $\text{GF}(2^n)$  angesehen werden.
• Die Basisvektoren  $\underline{g}_1$,  $\underline{g}_2$,  ...  , $\underline{g}_k$  sind linear unabhängig.
  

Der Untervektorraum  $\mathcal{C}$  wird aber nicht nur durch die Basisvektoren

$$\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}$$

aufgespannt, sondern andere Basisvektoren  $\underline{g}\hspace{0.05cm}'_1$,  $\underline{g}\hspace{0.05cm}'_2$  und  $\underline{g}\hspace{0.05cm}'_3$  sind ebenso geeignet, so lange zwischen diesen die lineare Unabhängigkeit gewährleistet ist.

$\text{Beispiel 5:}$  Wir vergleichen den Code  $\mathcal{C}$  von  $\text{Beispiel 4}$  mit einem zweiten Code  $\mathcal{C}\hspace{0.05cm}'$. Die Generatormatrizen lauten:

$$\boldsymbol{\rm G} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix}= \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} \boldsymbol{\rm G}\hspace{0.05cm}' = \begin{pmatrix} \underline{g}\hspace{0.05cm}'_1\\ \underline{g}\hspace{0.05cm}'_2\\ \underline{g}\hspace{0.05cm}'_3\\ \end{pmatrix}= \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix}\hspace{0.05cm}.$$

• Die beiden Codes sind identisch:   Sie beinhalten die genau gleichen Codeworte; es gilt nur eine andere Zuordnung.
• Bei dem Übergang von  $\boldsymbol{\rm G}$  auf  $\boldsymbol{\rm G}\hspace{0.05cm}'$  wurden folgende erlaubte Operationen ausgeführt:

$$\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_2 = \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.$$

• Zum entsprechenden Code  $\mathcal{C}'$  kommt man mit der Gleichung  $\underline{x}' = \underline{u} \cdot \boldsymbol{\rm G}'$:

$$\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = (0, 0, 0, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_0 \hspace{0.05cm},$$

$$\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},$$

$$\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_2 = (0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},$$

$$\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_1\hspace{0.05cm},$$

$$\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_4 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_6 \hspace{0.05cm},$$

$$\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_5\hspace{0.05cm},$$

$$\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_6 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_4\hspace{0.05cm},$$

$$\underline{u}_7 = (1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.$$

• Die entsprechenden Codeworte  $\underline{x}_i = \underline{u}_i \cdot \boldsymbol{\rm G}$  des Codes  $\mathcal{C}$   ⇒   Generatormatrix  $\boldsymbol{\rm G}$  sind im  $\text{Beispiel 4}$  (vorherige Seite) angegeben.

$\text{Fazit:}$  Die Codetabellen von  $\text{Beispiel 4}$  und  $\text{Beispiel 5}$  machen deutlich:

• $\mathcal{C}$  und  $\mathcal{C}\hspace{0.05cm}'$  beinhalten die genau gleichen Codeworte. Sie sind damit  identische Codes  und besitzen beide die gleiche Korrekturfähigkeit (siehe nächste Seite).
  

• $\mathcal{C}\hspace{0.05cm}'$  ist nun ein  systematischer Code, da die ersten  $k$  Binärstellen eines jeden Codewortes  $\underline{x}\hspace{0.05cm}'_i$  mit den Binärstellen des Informationswortes  $\underline{u}_i$  übereinstimmen.

Systematische Codes

Die Eigenschaft „systematisch” soll nun noch in mathematischer Form angegeben werden.

$\text{Definition:}$  Bei einem  $\text{systematischen }(n, k)–\text{Blockcode} \ \ \mathcal{C}$  beinhaltet jedes Codewort  $\underline{x}$  explizit das Informationswort  $\underline{u}$.

• Das heißt, es gilt:   $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k) \hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm} = (u_1, u_2, ... \hspace{0.05cm}, u_k, x_{k+1}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)\hspace{0.05cm}.$

• Die Generatormatrix hat in diesem Fall die Form  $\boldsymbol{\rm G_{\rm sys} } =\left({ \boldsymbol{\rm I}_{\rm k} \ ; \ \boldsymbol{\rm P} }\right)$  mit der  $k×k$–Einheitsmatrix  $\boldsymbol{\rm I}_{\rm k}$  und einer geeignet zu wählenden  $(n-1)×k$–Matrix  $\boldsymbol{\rm P}$.

Für das  $\text{Beispiel 5}$  auf der letzten Seite kann also auch geschrieben werden:

$$\boldsymbol{\rm G_{sys}} =\left({ \boldsymbol{\rm I}}_3 \: ; \: { \boldsymbol{\rm P}}\right)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} { \boldsymbol{\rm I_{3}}} = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.3cm}{\rm und}\hspace{0.3cm} { \boldsymbol{\rm P}} = \begin{pmatrix} 0 &1 \\ 1 &0 \\ 0 &0 \end{pmatrix}\hspace{0.05cm}.$$

Erfreulich aus Sicht der Kanalcodierung ist, dass für jeden Code  $\mathcal{C}$  ein systematischer (identischer oder zumindest äquivalenter) Code  $\mathcal{C}_{\rm sys}$  gefunden werden kann.

Beim  identischen systematischen Code  beinhalten  $\underline{x}$  und  $\underline{x}_{\rm sys}$  die gleichen Codeworte, nur die Zuordnung  $\underline{u}   →   \underline{x}$  ist unterschiedlich. Man kommt durch folgende Manipulationen bezüglich der Generatormatrix  $\boldsymbol{\rm G}$  von einem Blockcode  $\mathcal{C}$  zum identischen systematischen Code  $\mathcal{C}_{\rm sys}$:

• Vertauschen oder Permutieren der Zeilen,
  

• Multiplizieren aller Zeilen mit einem konstanten Vektor ungleich  $\underline{0}$,
  

• Ersetzen einer Zeile durch eine Linearkombination zwischen dieser Zeile und einer anderen.
  

$\text{Ohne Beweis:}$  Ein $\text{identischer systematischer Code }\mathcal{C}_{\rm sys}$ kann immer dann gefunden werden, wenn zu einer Generatormatrix  $\boldsymbol{\rm G}$  eine Matrix  $\boldsymbol{\rm A}$  existiert, so dass  $\boldsymbol{\rm G}_{\rm sys} = \boldsymbol{\rm A} \cdot \boldsymbol{\rm G}$  gilt.

Ist dies nicht möglich, so findet man zumindest durch Vertauschen oder Permutieren der Spalten von  $\boldsymbol{\rm G}$  einen  äquivalenten systematischen Code:

$$\mathcal{C}_{\rm sys} = {\rm \pi} (\mathcal{C})\hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\rm \pi}():\hspace{0.15cm}{\rm Permutationsoperator}\hspace{0.05cm}.$$

Die Codes  $\mathcal{C}$  und  $\mathcal{C}_{\rm sys}$  beinhalten dann zwar andere Codeworte, aber sie zeigen gleiche Eigenschaften. Beispielsweise weist  $\mathcal{C}_{\rm sys}$  in diesem Fall die gleiche minimale Hamming–Distanz  $d_{\rm min}$  auf wie der Code  $\mathcal{C}$.

$\text{Beispiel 6:}$  Wir betrachten die Generatormatrizen

$$\boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &0 \\ 0 &0 &1 &1 \end{pmatrix}\hspace{0.3cm}{\rm und}\hspace{0.3cm} \boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &1 &0 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

Die Analyse zeigt:

• Die zugehörigen Codes  $\mathcal{C}$  und  $\mathcal{C}_{\rm sys}$  beinhalten unterschiedliche Codeworte und sind somit auch nicht identisch:

$$\mathcal{C} = \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 0, 1, 1) \hspace{0.05cm},(1, 1, 0, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm},$$

$$\mathcal{C}_{\rm sys}= \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 1, 0, 1) \hspace{0.05cm},(1, 0, 1, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm}.$$

• Aber sie sind äquivalent:   $\boldsymbol{\rm G}_{\rm sys}$  ergibt sich aus  $\boldsymbol{\rm G}$  durch Vertauschen der zweiten und dritten Spalte.
• Es handelt sich in beiden Fällen um einen  $\text{(4, 2, 2)}$–Blockcode   ⇒   $d_{\rm min} = 2$.

Zusammenhang zwischen Generator– und Prüfmatrix

Zur Definition dieser beiden Beschreibungsmatrizen gehen wir von folgenden Gleichungen aus:

$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x}^{\rm T} = { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} \hspace{0.05cm}, \hspace{0.8cm} { \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T} = { \boldsymbol{\rm 0}}\hspace{0.05cm}.$$

Verknüpft man diese zwei Gleichungen, so erhält man:

$${ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.$$

Anzumerken ist, dass in diesen Gleichungen

• $\underline{0}$  einen Zeilenvektor mit  $k$  Elementen bezeichnet und
• $\boldsymbol{\rm 0}$  eine Matrix mit  $m$  Zeilen und  $k$  Spalten angibt,

wobei alle Elemente von  $\underline{0}$  und  $\boldsymbol{\rm 0}$  identisch Null sind.

$\text{Beispiel 7:}$  Wir betrachten wie im  $\text{Beispiel 4}$  den  $\text{(5, 3)}$–Blockcode

$$\mathcal{C} = \big \{ \hspace{0.15cm} ( \hspace{0.05cm} 0, 0, 0, 0, 0) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm} 0, 1, 1, 1, 0) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm}0, 1, 0, 1, 0) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm}0, 0, 1, 0, 0) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm} 1, 1, 0, 1, 1) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm}1, 0, 1, 0, 1) \hspace{0.05cm},$$

$$\hspace{0.6cm}( \hspace{0.05cm}1, 0, 0, 0, 1) \hspace{0.05cm},$$

$$\hspace{0.6cm}(\hspace{0.05cm}1, 1, 1, 1, 1) \big \}\hspace{0.05cm}.$$

Aus  $n= 5$  und  $k = 3$  folgt für die Anzahl der Prüfgleichungen  $m = 2$. Durch Analyse der möglichen Codeworte erhält man folgende Ergebnisse:

$$x_1 \oplus x_5 = 0 \hspace{0.05cm},\hspace{0.5cm} x_2 \oplus x_4 = 0\hspace{1cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix}$$

$$\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot { \boldsymbol{\rm G} }^{\rm T} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 1 &1 &1 \\ 0 &0 &1 \\ 1 &1 &1 \\ 1 &0 &0 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \\ 0 &0 &0 \end{pmatrix}\hspace{0.05cm}.$$

Die Nullmatrix besteht hier aus  $m = 2$  Zeilen und  $k = 3$  Spalten. Beispielsweise gilt für das Element in der ersten Zeile und der ersten Spalte:

$$1 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 0 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 1 \cdot 1 = 0 \hspace{0.05cm}.$$

Generatormatrix vs. Prüfmatrix bei systematischen Codes

Im allgemeinen Fall können  $\boldsymbol{\rm G}$  und  $\boldsymbol{\rm H}$  nicht direkt ineinander umgerechnet werden, schon allein aufgrund der unterschiedlichen Dimensionen von Generatormatrix  $(k \times n)$  und Prüfmatrix  $(m \times n)$.

$\text{Ohne Beweis:}$  Der Rechengang vereinfacht sich, wenn die  $(k \times n)$ –Generatormatrix in systematischer Form vorliegt:   $\boldsymbol{\rm G_{sys} } =\left({ \boldsymbol{\rm I} }_k \: ; \: { \boldsymbol{\rm P} }\right)$. Dann folgt aus  $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$  für die  $(m \times n)$–Prüfmatrix mit  $m = n-k$:

$${ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right) \hspace{0.05cm}.$$

Diese Gleichung gilt allgemein, also auch im nichtbinären Fall. Da wir uns im gesamten ersten Hauptkapitel auf binäre Codes beschränken ⇒   $\mathcal{C} \in \text{GF}(2^n)$, gilt  $- \boldsymbol{\rm P} = +\boldsymbol{\rm P}$, und man erhält die Form, die wir im Weiteren verwenden.

$${ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)=\left( { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)\hspace{0.05cm}.$$

$\text{Beispiel 8:}$  Wir betrachten weiterhin den beispielhaften  $\text{(5, 3)}$–Blockcode, gehen aber nun von der systematischen Generatormatrix  $\boldsymbol{\rm G}_{\rm sys}$  aus, die wir im  $\text{Beispiel 5}$  ermittelt haben:

$$\boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix} =\left({ \boldsymbol{\rm I} }_3 \: ; \: { \boldsymbol{\rm P} }\right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm I_3} }= \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix}, \hspace{0.3cm} { \boldsymbol{\rm P} }= \begin{pmatrix} 0 &1 \\ 1 &0\\ 0 &0 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm P}^{\rm T} } = \begin{pmatrix} 0 &1 &0\\ 1 &0 &0 \end{pmatrix}\hspace{0.05cm}.$$

Damit erhält man für die Prüfmatrix

$${ \boldsymbol{\rm H} } =\left({ \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_2 \right) = \begin{pmatrix} 0 &1 &0 &1 &0\\ 1 &0 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$

und es ergibt sich folgende Codetabelle:

$$\underline{u}_0 = (0, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_4 = (1, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_4 = (1, 0, 0, 0, 1) \hspace{0.05cm},$$

$$\underline{u}_1 = (0, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_1 = (0, 0, 1, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_5 =(1, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_5 = (1, 0, 1, 0, 1)\hspace{0.05cm},$$

$$\underline{u}_2 =(0, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_6 =(1, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_6 = (1, 1, 0, 1, 1)\hspace{0.05cm},$$

$$\underline{u}_3 = (0, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_7 = (1, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_7 = (1, 1, 1, 1, 1) \hspace{0.05cm}.$$

Zusammen mit dem Vektor  $\underline{x} = (u_1, u_2, u_3, p_1, p_2) = (x_1, x_2, x_3, x_4, x_5)$  lauten dann die Prüfbits:

$$p_1 = u_2 \hspace{0.05cm},\hspace{0.2cm}p_2 = u_1 \hspace{0.05cm},$$

und die entsprechenden Prüfgleichungen des Decoders:

$$x_2 + x_4 = 0 \hspace{0.05cm},\hspace{0.2cm}x_1 + x_5 = 0 \hspace{0.05cm}.$$

Man erkennt aus diesen Gleichungen und auch aus obiger Codetabelle:

• Dieser Code bietet gegenüber einem Übertragungsfehler hinsichtlich des dritten Bits  $(x_3 = u_3)$  keinen Schutz.
• Damit ist natürlich weder eine Fehlererkennung und noch weniger Fehlerkorrektur möglich.
• Gleiches gilt aber auch für den nichtsystematischen Code entsprechend  $\text{Beispiel 7}$  auf der letzten Seite.

Darstellung von SPC und RC als duale Codes

Nun sollen für die bereits im Kapitel  Beispiele binärer Blockcodes  behandelten Codes noch jeweils die Generatormatrix  $\boldsymbol{\rm G}$  und die Prüfmatrix  $\boldsymbol{\rm H}$  angegeben werden. Die Codelänge sei für die folgenden Beispiele stets  $n = 5$, doch lassen sich die Ergebnisse auch für andere Codelängen in gleicher Weise interpretieren. Es gilt für

• den  Single–Parity–check Code   ⇒   $\text{SPC (5, 4)}$:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm};$$

• den  Wiederholungscode (Repetition Code)   ⇒   $\text{RC (5, 1)}$:

$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Die jeweils erste Gleichung lässt sich einfach aus der jeweiligen Definition herleiten und die abgeleitete Gleichung folgt aus der Beziehung  $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$.

Aus den obigen Matrizen kann verallgemeinert werden:

• Die Generatormatrix des  $\text{RC (5, 1)}$  ist identisch mit der Prüfmatrix des  $\text{SPC (5, 4)}$. Es handelt sich jeweils um  $(5 \times 1)$–Matrizen.
  

• Die Prüfmatrix des  $\text{RC (5, 1)}$  ist identisch mit der Generatormatrix des  $\text{SPC (5, 4)}$. Diese beiden Matrizen haben jeweils  $5$  Spalten und  $4$  Zeilen.
  

• Dieser Sachverhalt ergibt sich, weil es sich hier um so genannte „duale Codes” handelt. Zur Erklärung benötigen wir noch zwei Definitionen:
  

$\text{Definition:}$  Zwei lineare Codes  $\mathcal{C}$  und  $\mathcal{C}\hspace{0.05cm}'$, beide aus  ${\rm GF}(2^n)$, sind  orthogonal, wenn alle Codeworte  $\underline{x} \in \mathcal{C}$  zu allen Codeworten  $\underline{x}\hspace{0.05cm}' \in \mathcal{C}\hspace{0.05cm}'$  orthogonal sind. Man bezeichnet dann  $\mathcal{C}$  und  $\mathcal{C}\hspace{0.05cm}'$  als duale Codes.

$\text{Definition:}$  Zwei Codeworte  $\underline{x} \in{\rm GF}(2^n)$  und  $\underline{x\hspace{0.05cm}'} \in {\rm GF}(2^n)$  sind immer dann zueinander  orthogonal, wenn das  innere Produkt  verschwindet:

$$\big \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \big \rangle = \sum_{i=1 }^{n} x_i \cdot x\hspace{0.05cm}'_i = 0 \hspace{0.05cm}, \hspace{0.5cm} \left \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \right \rangle \in {\rm GF}(2^n) \hspace{0.05cm}.$$

Wegen der Produktbildung in  ${\rm GF}(2^n)$  sind auch folgende Codewort–Paare zueinander orthogonal:

$$\left \langle \hspace{0.05cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.5cm} (1, 1, 1, 0) \hspace{0.05cm} \right \rangle = 0\hspace{0.05cm},\hspace{0.2cm} \left \langle \hspace{0.1cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (0, 1, 1, 0) \hspace{0.1cm}\right \rangle = 0\hspace{0.05cm}.$$

• Der Code  $\mathcal{C}$  spannt einen  $k$–dimensionalen Untervektorraum in  ${\rm GF}(2^n)$  auf.
• Der Untervektorraum des dualen Codes  $\mathcal{C}\hspace{0.05cm}'$  ist zu diesem orthogonal und weist die Dimension  $n-k$  auf.
• Damit gilt:   ${\rm dim} \{ \mathcal{C} \} + {\rm dim} \{ \mathcal{C}\hspace{0.05cm}' \} = n\hspace{0.05cm}.$
  

Einige Eigenschaften des (7, 4, 3)–Hamming–Codes

Fassen wir die bisherigen Ergebnisse dieses Kapitels am Beispiel des systematischen Hamming–Codes nochmals zusammen,  der bereits im Kapitel  "Beispiele binärer Blockcodes"  ausführlich beschrieben wurde.  Dieser  $\text{(7, 4, 3)}$–Code ist gekennzeichnet durch

Codeworte des  $\text{HC (7, 4, 3)}$

• die Anzahl der Prüfgleichungen:  $m = 3$,
  

• die Codelänge  $n = 2^m-1 = 7$,
  

• die Informationswortlänge  $k = n-m = 4$,
  

• die Anzahl  $2^k =16$  der Codeworte  (Dimension),
  

• die Rate  $R= k/n = 4/7$,
  

• die minimale Distanz  $d_{\rm min} = 3$  $($unabhängig von  $m$,  $n$  und  $k)$.
  

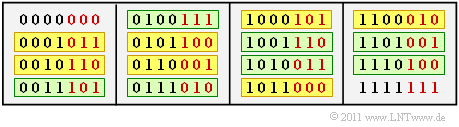
In obiger Tabelle sind die  $2^4 = 16$  Codeworte angegeben
(schwarz:  vier Informationsbits, rot:  drei Prüfbits).

Man erkennt daraus:

• Der Code beinhaltet sowohl das Null–Wort  "$0000000$"  als auch das Eins–Wort  "$1111111$".

• Es gibt sieben Codeworte,  die sich aus  "$0001011$"  jeweils durch zyklische Verschiebung ergeben  (alle gelb hinterlegt).

• Es gibt sieben Codeworte,  die sich aus  "$0011101$"  jeweils durch zyklische Verschiebung ergeben  (alle grün hinterlegt).

• Zu jedem Codewort existiert auch das  "negierte Codewort",  zum Beispiel gibt es neben  "$0001011$"  auch das Codewort  "$1110100$".

• Die Prüfmatrix kann wie folgt geschrieben werden:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}=\left({ \boldsymbol{\rm P}}^{\rm T} \: ; \: { \boldsymbol{\rm I}}_3 \right)\hspace{0.8cm} \Rightarrow\hspace{0.8cm}{ \boldsymbol{\rm P}}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 \\ 0 &1 &1 &1 \\ 1 &1 &0 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm}{ \boldsymbol{\rm I}}_3 = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$

• Dementsprechend gilt für die Generatormatrix:

$${ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_4 \: ; \: { \boldsymbol{\rm P}}\right) = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &1\\ 0 &0 &1 &0 &1 &1 &0\\ 0 &0 &0 &1 &0 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$

Aufgaben zum Kapitel

Aufgabe 1.7: Prüfmatrix und Generatormatrix des HC (7, 4, 3)

Aufgabe 1.7Z: Klassifizierung von Blockcodes

Aufgabe 1.8: Identische Codes

Aufgabe 1.8Z: Äquivalente Codes

Aufgabe 1.9: Erweiterter Hamming–Code

Aufgabe 1.9Z: Erweiterung und/oder Punktierung

Aufgabe 1.10: Einige Generatormatrizen