Allgemeine Beschreibung von OFDM

Inhaltsverzeichnis

1 Das Prinzip von OFDM – Systembetrachtung im Zeitbereich
2 Systembetrachtung im Frequenzbereich bei akausalem Grundimpuls
3 Systembetrachtung im Frequenzbereich bei kausalem Grundimpuls
4 Orthogonalitätseigenschaften der Träger
5 Aufgaben zum Kapitel

Das Prinzip von OFDM – Systembetrachtung im Zeitbereich

"Orthogonal Frequency Division Multiplex" $\rm (OFDM)$ ist ein digitales Mehrträger–Modulationsverfahren mit folgenden Eigenschaften:

Prinzip eines auf

$\text{4-QAM}$ basierenden

$\rm OFDM$ -Senders

Statt eines breitbandigen, stark modulierten Signals werden zur Datenübertragung eine Vielzahl schmalbandiger, zueinander orthogonaler Unterträger verwendet. Dies ermöglicht unter anderem die Anpassung an einen frequenzselektiven Kanal.

Die Modulation der Unterträger selbst erfolgt bei OFDM üblicherweise durch eine herkömmliche Quadratur–Amplitudenmodulation $\rm (QAM)$ oder durch binäre Phasenmodulation $\rm (BPSK)$ , wobei sich die einzelnen Träger hinsichtlich der Modulationsart durchaus unterscheiden können.

Unterschiede im Modulationsgrad führen dabei zu verschieden hohen Datenraten der Unterträger. Das heißt also, dass ein hochratiges Quellensignal zur Übertragung in mehrere Signale von deutlich niedrigerer Symbolrate aufgespaltet werden muss.

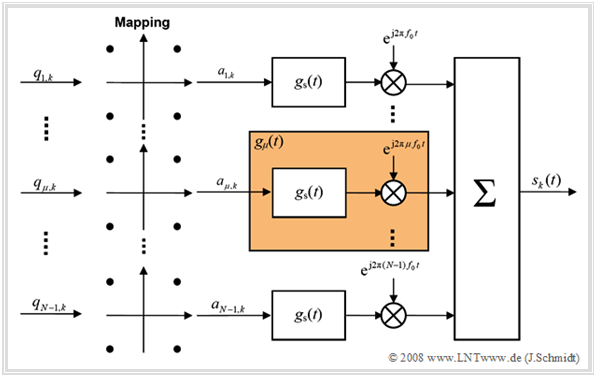
Die Grafik zeigt das Grundprinzip eines OFDM–Senders, basierend auf $\text{4-QAM}$ .

Die Darstellung des „nullten” Zweiges $(\mu = 0)$ , der den Gleichanteil darstellt, wurde hier bewusst weggelassen, da dieser häufig zu Null gesetzt wird ⇒ für alle Rahmen $k$ gilt $a_{0,\hspace{0.08cm} k} =0$ .
Die $N–1$ Teile des zur Zeit $k$ anliegenden Datenstroms $〈q_{\mu,k}〉$ werden zunächst 4–QAM–codiert, indem jeweils zwei Bit zusammengefasst werden. Danach wird die im allgemeinen komplexe Amplitude $a_{\mu,\hspace{0.08cm}k}$ $($ mit Laufvariablen $\mu = 1$ , ... , $N–1)$ impulsgeformt und mit dem $\mu$ –ten Vielfachen der Grundfrequenz $f_0$ moduliert.
Das Sendesignal ist nun die additive Überlagerung der einzelnen Teilsignale. Die Betrachtung erfolgt hier und auch im Folgenden im äquivalenten Tiefpassbereich, wobei auf den Index „TP” verzichtet wird.
Das Impulsformfilter $g_s(t)$ ist ein auf den Bereich $0 ≤ t < T$ begrenztes Rechteck der Höhe $s_0$ . Wir nennen $T$ die Symboldauer und bezeichnen den Kehrwert $f_0 = 1/T$ als die Grundfrequenz.

Fasst man dieses Filter nun mit der jeweiligen Modulation zu

$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$

mit $\mu ∈ \{0, \ \text{...}\ , N–1\}$ zusammen, so ergibt sich das OFDM–Sendesignal $s_k(t)$ im $k$ –ten Zeitintervall:

$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$

Das gesamte OFDM–Sendesignal unter Berücksichtigung aller Zeitintervalle lautet dann:

$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R} } )} }.$

$T_{\rm R}$ bezeichnet die Rahmendauer. Innerhalb dieser Zeit liegen die gleichen Daten am Eingang an und nach $T_{\rm R}$ folgt der nächste Rahmen.

Die Symboldauer $T$ ergibt sich bei einem Mehrträgersystem mit $M$ QAM–Signalraumpunkten und der Bitdauer $T_{\rm B}$ der binären Quellensysmbole allgemein zu

$T = N \cdot {\rm{log}_2}(M) \cdot T_{\rm{B} } ,$

wobei

$N$ wieder die Anzahl der Unterträger angibt.

Für die Rahmendauer muss $T_{\rm R} \ge T$ gelten. Zunächst gelte $T_{\rm R} = T$ .

$\text{Beispiel 1:}$

Wir gehen zunächst von einem Einträgersystem mit der Datenrate $R_{\rm B} = 768 \ \rm kbit/s$ ⇒ $T_{\rm B} ≈ 1.3 \ \rm µ s$ und einem Mapping mit $M = 4$ Signalraumpunkten $\text{(4–QAM)}$ aus. Die Symboldauer im Einträgerfall $($ "Single Carrier", $\rm SC)$ beträgt dann:

$T_\text{SC} = 1 \cdot {\rm{log}_2}(4) \cdot 1.3 \,{\rm{µ s} } \approx 2.6 \,{\rm{µ s} }.$

Unter der Annahme, dass für ein Mehrträgersystem $($ "Multi Carrier"', $\rm MC)$ mit $N = 32$ Trägern das Modulationsverfahren $\text{16–QAM}$ verwendet wird, ergibt sich eine um den Faktor $64$ größere Symboldauer:

$T_\text{MC} = 32 \cdot {\rm{log}_2}(16) \cdot 1.3 \,{\rm{µ s} } \approx 0.167\, {\rm{ms} }.$

$\text{Fazit:}$

Die Dauer eines Symbols erhöht sich bei einem Mehrträgersystem im Vergleich zu einem Einzelträgersystem deutlich, wodurch der störende Einfluss der Kanalimpulsantwort verringert wird und die Impulsinterferenzen abnehmen.

Die Möglichkeit, für verschiedene Teilbänder unterschiedlich robuste Modulationsverfahren einzusetzen, ist einer der großen Vorteile von OFDM. Hierauf wird in den Abschnitten OFDM für 4G–Netze und Digital Subscriber Line $\rm (DSL)$ noch genauer eingegangen.

Systembetrachtung im Frequenzbereich bei akausalem Grundimpuls

Wir betrachten nochmals das OFDM–Sendesignal im $k$ –ten Zeitintervall, wobei wir wieder $T_{\rm R} = T$ setzen:

$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T)}.$

Den Grundimpuls $g_{\mu}(t)$ nehmen wir vereinfachend symmetrisch um $t = 0$ an. Dann gilt mit $f_0 = 1/T$ :

Spektrum eines akausalen Grundimpulses

$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad \quad - T/2 < t < T/2, \\ 0 \quad \quad \quad \quad \quad \quad \; {\rm sonst.} \\ \end{array} \right.$

Im Spektralbereich korrespondiert eine solche akausale und mit einer (komplexen) Exponentialfunktion der Frequenz $\mu · f_0$ modulierte Rechteckfunktion mit einer um $\mu · f_0$ verschobenen $\rm si$ –Funktion:

$G_\mu (f) = s_0 \cdot T \cdot {\rm{si}} \big(\pi T (f - \mu f_0 ) \big ).$

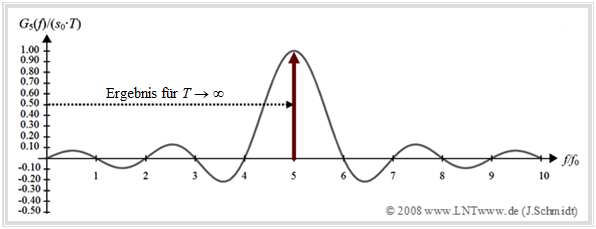
Rechts ist diese Spektralfunktion $($ normiert auf das Maximum $s_0 · T)$ für $\mu = 5$ dargestellt.

Der Pfeil soll andeuten, dass bei zeitlich unbeschränktem Grundimpuls die dargestellte $\rm si$ –Funktion durch einen Dirac–Impuls an der Stelle $\mu · f_0$ zu ersetzen wäre.

$\text{Fazit:}$ Sind alle Amplitudenkoeffizienten $a_{μ,\hspace{0.08cm}k} ≠ 0$ , so setzt sich das Spektrum $S_k(f)$ des Sendesignals im $k$ –ten Zeitbereichsintervall aus $N$ um jeweils ein Vielfaches der Grundfrequenz $f_0$ verschobenen $\rm si$ –Funktionen zusammen. Die Funktion ${\rm si}(x) = \sin(x)/x$ wird oft als „Spaltfunktion” bezeichnet.

Systembetrachtung im Frequenzbereich bei kausalem Grundimpuls

$\text{Wichtiges Ergebnis:}$ Berücksichtigt man weiter, dass in der Realität von einem kausalen Grundimpuls

$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e} }^{ {\kern 1pt} {\rm{j{\kern 1pt}\cdot {\kern 1pt}2 \pi} } {\kern 1pt}\cdot {\kern 1pt} \mu f_0 {\kern 1pt}\cdot {\kern 1pt}t} \quad 0 \le t < T, \\ 0\quad \quad \quad \quad \quad {\rm sonst}, \\ \end{array} \right.$

ausgegangen werden muss, so ergibt sich das Spektrum zu

$S_k (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot \,} {\rm{si} }\big(\pi \cdot T(f - \mu \cdot f_0 )\big) \cdot {\rm{e} }^{ - {\rm{j2\pi} }\hspace{0.05cm}\cdot \hspace{0.05cm} {T}/{2} \hspace{0.05cm}\cdot \hspace{0.05cm} (f - \mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 )} .$

Die komplexe Exponentialfunktion kommt durch die Grenzen des hier zur Impulsformung verwendeten Rechtecks im Zeitbereich $0$ ... $T$ zustande
$($ Verschiebung um $T/2)$ .
Die vorher gezeigte rein reelle $\rm si$ –Funktion würde hingegen dem nichtkausalen Rechteck von $-T/2$ ... $+T/2$ entsprechen.

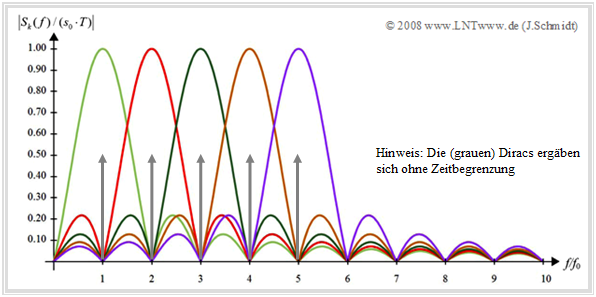
Die Grafik zeigt exemplarisch das Betragsspektrum eines OFDM–Signals mit fünf Trägern.

Betragsspektrum eines OFDM-Signals

Auffallend ist, dass das Maximum eines jeden Subträgers mit den Nullstellen aller anderen Träger zusammenfällt. Dies entspricht der ersten Nyquistbedingung im Frequenzbereich.
Diese Eigenschaft ermöglicht eine ICI–freie Abtastung (das heißt: ohne "Intercarrier–Interferenz") des Spektrums bei Vielfachen von $f_0$ . Die Orthogonalität ist also gewährleistet.
Würde man auf die Zeitbegrenzung bei der Impulsformung verzichten, so würden aus den dargestellten $\rm si$ –Funktionen im Abstand $f_0$ jeweils Diraclinien (in der Grafik grau eingezeichnet).
Diese idealisierende Vereinfachung ist in der Praxis leider nicht umsetzbar. Die Forderung $T → ∞$ bedeutet nämlich gleichzeitig, dass in unendlich langer Zeit nur ein einziger Rahmen übertragen werden könnte.

$\text{Fazit:}$ Ein OFDM–Signal unter der Voraussetzung einer rechteckförmigen Impulsformung und eines Unterträgerabstandes von $f_0$

erfüllt die erste Nyquistbedingung im Zeitbereich und
dadurch natürlich ebenso die erste Nyquistbedingung im Frequenzbereich.

Orthogonalitätseigenschaften der Träger

Die Zeitbegrenzung des Grundimpulses ermöglicht die separate Betrachtung der beiden Summen in der Gleichung des OFDM–Sendesignals:

$s(t) = \sum\limits_{k = - \infty }^{+\infty} {s_k (t)} \quad {\rm{mit}} \quad s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T )}.$

Der $k$ –te Sendeimpuls ist dabei die Summe der um $k · T$ verschobenen Grundimpulse $g_{\mu}(t)$ , die jeweils mit den $\mu$ –ten Amplitudenkoeffizienten des QAM–Coders zum Zeitpunkt $k$ gewichtet werden.

$\text{Noch ein wichtiges Ergebnis:}$

Damit ergibt sich für das Spektrum $S_{\mu,\hspace{0.08cm}k}(f)$ des $\mu$ –ten Trägers im $k$ –ten Intervall:

$S_{\mu ,\hspace{0.08cm}k} (f) = s_0 \cdot a_{\mu ,\hspace{0.08cm}k} \cdot T \cdot {\rm{si} }\big(\pi \cdot T(f - \mu \cdot f_0 )\big) \cdot {\rm{e} }^{ - {\rm{j \hspace{0.05cm} \cdot \hspace{0.05cm} \pi} } \hspace{0.05cm} \cdot \hspace{0.05cm}T \hspace{0.05cm} \cdot \hspace{0.05cm} (f - \mu \hspace{0.05cm} \cdot \hspace{0.05cm} f_0)}.$

Dabei gelten folgende für das OFDM-Prinzip wichtige Eigenschaften:

Die Sendeimpulse $s_k(t)$ sind zueinander orthogonal in der Zeit $($ Laufvariable $k)$ , da sie sich durch die Zeitbegrenzung des Formfilters $g_s(t)$ nicht überlappen.
Die zeitliche Begrenzung der Impulse führt zwar zu einer spektralen Überlappung, dennoch besteht auch Orthogonalität bezüglich der Träger $($ Laufvariable $\mu)$ , da:

$S_k (\mu \cdot f_0 ) = S_{\mu ,\hspace{0.08cm}k} (\mu \cdot f_0 ) = s_0 \cdot a_{\mu ,\hspace{0.08cm}k} \cdot T.$

$\text{Beweis:}$ Für die Orthogonalität an den Frequenzstützstellen $\mu · f_0$ muss gelten:

$S(\mu \cdot f_0 ) = S_0 (\mu \cdot f_0 ) + \ \text{...} \ + S_\mu (\mu \cdot f_0 ) + \ \text{...} \ + S_{N - 1} (\mu \cdot f_0 ) = S_\mu (\mu \cdot f_0 ).$

Hier und im Folgenden wird auf den Index $k$ der Rahmennummer verzichtet. Aus

$s_\mu (t) = s_0 \cdot a_\mu \cdot {\rm{e} }^{{\rm j \hspace{0.03cm}\cdot\hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} \mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{rect} } \left( {\frac{ {t - T/2} }{T} } \right) \hspace{0.15cm} {\rm{und }} \hspace{0.15cm} S_\mu (f) = \int_{ - \infty }^{+\infty} {s_\mu (t) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t}$

ergibt sich das Spektrum

$S(f)$ allgemein zu:

$S(f) = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{si} }({\rm{\pi } }f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{\rm{0} } \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \text{...}$

$\hspace{0.5cm}\text{...} + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{si} } ({\rm{\pi } } f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm}{T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{ {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm}\mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \text{...}$

$\hspace{0.5cm}\text{...} +\left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{si} } ({\rm{\pi } }f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{ {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm}(N-1) \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} .$

Mit Distributionen lässt sich diese Gleichung wie folgt ausdrücken:

$S(f) = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{si} }({\rm{\pi } }f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f) \hspace{0.08cm}+ \text{...}$

$\hspace{0.5cm} \text{...} + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{si} } ({\rm{\pi } } fT )\cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f - \mu \cdot f_0 )\hspace{0.08cm}+ \text{...}$

$\hspace{0.5cm} \text{...} + \left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{si} } ({\rm{\pi } } f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \delta (f-(N - 1) \cdot f_0 ) .$

$\Rightarrow \hspace{0.3cm}S(f) = {s_0 \cdot a_0 \cdot T \cdot {\rm{si} }({\rm{\pi } } \cdot T \cdot f) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \hspace{0.08cm}+\hspace{0.08cm} \text{...}$

$\hspace{1.4cm}\text{...} + {s_0 \cdot a_\mu \cdot T \cdot {\rm{si} } ({\rm{\pi } } \cdot T \cdot (f - \mu \cdot f_0 ))\cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} (f - \mu \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 )} } \hspace{0.08cm}+ \hspace{0.08cm}\text{...}$

$\hspace{1.4cm}\text{...} + s_0 \cdot a_{N - 1} \cdot T \cdot {\rm si } ({\rm \pi } \cdot T \cdot \big [f-(N - 1) \cdot f_0 ) \big ] \cdot {\rm e}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\hspace{0.03cm}\cdot \hspace{0.03cm} \big [f-(N - 1) \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 \big ]}.$

Setzt man nun $f = \mu · f_0$ , so erhält man:

$S (\mu \cdot f_0) = 0 \hspace{0.08cm}+ \hspace{0.08cm} \text{...} \hspace{0.08cm}+\hspace{0.08cm} s_0 \cdot a_\mu \cdot T \cdot {\rm{si} } (0) \cdot {\rm{e} }^0 \hspace{0.08cm}+\hspace{0.08cm} \text{...}+ 0 = s_0 \cdot a_\mu \cdot T = S_\mu ( \mu \cdot f_0 ).$

Das Spektrum bei $f = \mu · f_0$ setzt sich also nur aus Anteilen des $\mu$ –ten Trägers zusammen, wobei alle anderen Träger identisch Null werden.
Die Orthogonalität ist gewährleistet.
q.e.d.

$\text{Fazit:}$ Die Orthogonalität des OFDM–Signals $s(t)$ ist sowohl für die Laufvariable $k$ $\rm (Zeit)$ als auch für die Laufvariable $\mu$ $\rm (Trägerfrequenzen)$ gegeben!

Aufgaben zum Kapitel

Aufgabe 5.6: OFDM–Spektrum

Aufgabe 5.6Z: Einträger–und Mehrträgersystem