Aufgabe 1.2Z: Linear verzerrendes System

• Zurück zum Buch

Zur Herleitung der Verzerrungen
bei Rechtecksignalen

Modulator, Kanal und Demodulator einer Einrichtung zur Nachrichtenübertragung können durch ein einziges lineares System mit dem Frequenzgang

$$H(f) = {\rm si }( \pi \cdot f \cdot \Delta t)$$

beschrieben werden.  Die dazugehörige Impulsantwort ist rechteckförmig,  symmetrisch um  $t = 0$  und weist die Höhe  $1/Δt$  sowie die (äquivalente) Dauer  $Δt$  auf:

$$h(t) = \left\{ \begin{array}{c} 1/\Delta t \\ 1/(2\Delta t) \\ 0 \\ \end{array} \right. \begin{array}{*{4}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| < \Delta t/2,} \\ {\left| \hspace{0.005cm}t\hspace{0.05cm} \right| = \Delta t/2,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > \Delta t/2.} \\ \end{array}$$

Es handelt sich um einen Spalttiefpass, der im Kapitel  Einige systemtheoretische Tiefpassfunktionen  des Buches „Lineare zeitinvariante Systeme” behandelt wurde.

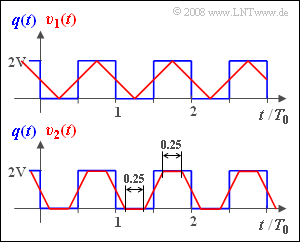
Am Systemeingang liegt das periodische Rechtecksignal  $q(t)$  mit der Periodendauer  $T_0$  an.  Die Dauer der einzelnen Rechtecke und die der Lücken sind somit jeweils  $T_0/2$.  Die Höhe der Rechtecke beträgt  $2\ \rm V$.

Das Signal  $v(t)$  am Systemausgang wird als Sinkensignal bezeichnet.  Dieses ist für zwei verschiedene Parameterwerte für die äquivalente Impulsdauer in der Grafik dargestellt (rote Kurvenverläufe):

• Das Signal  $v_1(t)$  ergibt sich,  wenn die äquivalente Impulsdauer von  $h(t)$  genau  $Δt_1$  ist.
• Entsprechend ergibt sich das Signal  $v_2(t)$  mit der äquivalenten Impulsdauer  $Δt_2$.

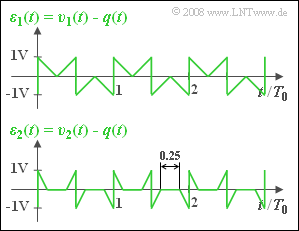
Die Veränderung vom Rechtecksignal  $q(t)$  zum dreieck- bzw. trapezförmigen Sinkensignal  $v(t)$  ist auf lineare Verzerrungen zurückzuführen und wird durch das Fehlersignal  $ε(t) = v(t) - q(t)$  erfasst.

Mit den Leistungen  $P_q$  und  $P_ε$  der Signale  $q(t)$  und  $ε(t)$  kann das Sinken–SNR berechnet werden:

$$\rho_{v} =P_{q}/{P_{\varepsilon }} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Qualitätskriterien.  Bezug genommen wird insbesondere auf die Seite  Signal-zu-Stör-Leistungsverhältnis  und auf das Kapitel  Lineare Verzerrungen  im Buch „Lineare zeitinvariante Systeme”.
• Die Leistungen  $P_q$  und  $P_ε$  sind die quadratischen Mittelwerte der Signale  $q(t)$  und  $ε(t)$  und können bei periodischen Signalen mit der Periodendauer  $T_0$  wie folgt ermittelt werden:

$$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$

• Die Angabe von Leistungen in  $\rm V^2$  bedeutet,  dass die Signale auf den Widerstand  $R = 1\ \rm \Omega$  bezogen werden.

Fragebogen

1

Wie groß ist die äquivalente Impulsdauer  $Δt_1$  innerhalb des Signals  $v_1(t)$,  bezogen auf die Periode  $T_0$?

$Δt_1/T_0 \ = \ $

2

Wie groß ist der Maximalwert des Fehlersignals  $ε_1(t) = v_1(t) - q(t)$?

$ε_\text{1, max} \ = \ $ $\ \rm V$

3

Wie groß ist die „Leistung”  $P_{ε1}$  des Fehlersignals,  also die mittlere quadratische Abweichung zwischen  $v_1(t)$  und  $q(t)$?

$P_{ε1} \ = \ $ $\ \rm V^2$

4

Berechnen Sie die Nutzleistung  $P_q$  und das Sinken–SNR  $ρ_{v1}$.

$P_q\ = \ $ $\ \rm V^2$

$ρ_{v1} \ = \ $

5

Wie groß ist die äquivalente Impulsdauer  $Δt_2$  innerhalb des Signals  $v_2(t)$,  bezogen auf die Periode  $T_0$?

$Δt_2/T_0 \ = \ $

6

Ermitteln Sie das Fehlersignal  $ε_2(t) = v_2(t) - q(t)$,  die Verzerrungsleistung  $P_{ε2}$  und das Sinken–SNR  $ρ_{v2}$.

$P_{ε2} \ = \ $ $\ \rm V^2$

$ρ_{v2} \ = \ $

7

Verallgemeinern Sie Ihre Ergebnisse für eine beliebige äquivalente Impulsdauer  $Δt$.  Welches Sinken–SNR  $ρ_{v3}$  ergibt sich für  $Δt_3 = T_0/20$?

$ρ_{v3} \ = \ $

Musterlösung

Musterlösung

(1)   Allgemein gilt  $v(t) = q(t) ∗ h(t)$.  Die Faltung des periodischen Rechtecksignals  $q(t)$  mit der ebenfalls rechteckigen Impulsantwort  $h(t)$  liefert nur dann ein Dreiecksignal  $v(t)$, wenn die miteinander gefalteten Rechtecke gleiche Breite haben. Daraus folgt:

$$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

Fehlersignale bei den beiden betrachteten Empfangsfiltern unterschiedlicher Breite

(2)   Das Fehlersignal  $ε_1(t)$  ist in nebenstehender Grafik oben dargestellt.  Man erkennt, dass  $ε_1(t)$  alle Werte zwischen  $±1 \ \rm V$  annehmen kann:

$${\varepsilon}_\text{ 1, max} \hspace{0.15cm}\underline {= {1}\;{\rm V}} \hspace{0.05cm}.$$

(3)   Es genügt die Mittelung über den Zeitbereich von  $t = 0$  bis  $t =T_0/4$, da alle anderen Teilintervalle genau gleiche Beiträge liefern:

$$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\int_{0}^{ T_{\rm 0}/4} {\varepsilon_1(t)^2 }\hspace{0.1cm}{\rm d}t = \frac{1 \,{\rm V}^2}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ T_{\rm 0}/4} {\left( 1 - \frac{t}{T_{\rm 0}/4}\right)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$

• Mit der Substitution  $x = 4 · t/T_0$  kann hierfür auch geschrieben werden:

$$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ 1} \hspace{-0.2cm}{\left( 1 - 2x + x^2\right)}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}= 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \left( 1 - 1 + \frac{1}{3}\right)\hspace{0.15cm}\underline {= 0.333} \,{\rm V}^2\hspace{0.05cm}.$$

(4)   Die Mittelung über eine Periode des quadrierten Quellensignals liefert:

$$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$

• Das Sinken–SNR beträgt somit

$$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$

(5)   Entsprechend der Skizze auf dem Angabenblatt wird nun aus einem Rechteck der Dauer  $0.5 \cdot T_0$  ein Trapez der absoluten Dauer  $0.75 · T_0$.

• Damit ist nach den Gesetzen der Faltung offensichtlich, dass die äquivalente Impulsdauer  $Δt_2/T_0\hspace{0.15cm}\underline { = 0.25}$  sein muss.

(6)   Die untere Skizze in obiger Grafik zeigt, dass sich  $ε_2(t)$  ebenso wie  $ε_1(t)$  innerhalb einer Periodendauer  $T_0$  aus vier Dreiecken zusammensetzt, doch sind diese nur halb so breit. 

• In der Hälfte der Zeit ist nämlich  $ε_2(t) = 0$.

• Wegen  $ε_\text{2, max} = ε_\text{1, max} = 1 \ \rm V$  erhält man:

$$P_{\varepsilon{\rm 2}} ={P_{\varepsilon{\rm 1}}}/{2} \hspace{0.15cm}\underline {= 0.167} \,{\rm V}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 2}} = {P_{q}}/{P_{\varepsilon {\rm 2}}}\hspace{0.15cm}\underline {= 12} \hspace{0.05cm}.$$

(7)   Für  $Δt = T_0/2$  wurde in der Teilaufgabe  (3)  die Verzerrungsleistung  $P_{ε1} = 1/3 \ \rm V^{ 2 }$  berechnet.

• In der Teilaufgabe  (6)  wurde gezeigt, dass bei  $Δt = T_0/4$  die Verzerrungsleistung  $P_{ε2}$  nur halb so groß ist.

• Anschaulich wurde erläutert, dass ein linearer Zusammenhang besteht.  Daraus folgen für  $Δt ≤ T_0/2$  die empirischen Gleichungen:

$$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$

• Der Sonderfall  $Δt = T_0/20$  führt somit zu den Resultaten:

$$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$