Kausale Systeme und Laplacetransformation

Applet in neuem Tab öffnen       English Version

Programmbeschreibung

Dargestellt werden reelle und symmetrische Tiefpässe  $H(f)$  und die dazugehörigen Impulsantworten  $h(t)$, nämlich

• Gauß–Tiefpass  (englisch:  Gaussian low–pass),
• Rechteck–Tiefpass   (englisch:  Rectangular low–pass),
• Dreieck–Tiefpass  (englisch:  Triangular low–pass),
• Trapez–Tiefpass  (englisch:  Trapezoidal low–pass),
• Cosinus–Rolloff–Tiefpass  (englisch:  Cosine-rolloff low–pass),
• Cosinus-Quadrat-Tiefpass  (englisch:  Cosine-rolloff -squared Low–pass).

Es ist zu beachten:

• Die Funktionen  $H(f)$  bzw.  $h(t)$  werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
• Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
• Die Abszissen  $t$  (Zeit) und  $f$  (Frequenz) sowie die Ordinaten  $H(f)$  und  $h(t)$  sind jeweils normiert.

Theoretischer Hintergrund

Betrachtetes Systemmodell

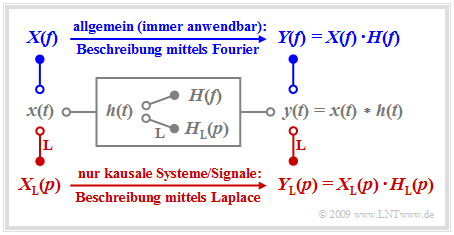
Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort  $h(t)$, an dessen Eingang das Signal  $x(t)$  anliegt.  Das Ausgangssignal  $y(t)$  ergibt sich dann als das Faltungsprodukt  $x(t) ∗ h(t)$.

Bei akausalen Systemen und Signalen muss zur Spektralbeschreibung stets das  erste Fourierintegral  angewendet werden, und es gilt für das Ausgangsspektrum:

Allgemeines (auch akausales) sowie kausales Systemmodell

$$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$

Das Fourierintegral besitzt auch für kausale Systeme und Signale weiterhin Gültigkeit, also für

$$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

In diesem Fall ergeben sich aber durch Anwendung der Laplace–Transformation unter Beachtung gewisser Restriktionen wesentliche Vorteile:

• Die so behandelten Systeme sind stets durch eine Schaltung realisierbar.  Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten.
• Die Laplace–Transformierte  $X_{\rm L}(p)$  ist stets eine reelle Funktion der Spektralvariablen  $p$.  Dass sich  $p = {\rm j} · 2πf$  aus der Multiplikation der physikalischen Kreisfrequenz  $ω = 2πf$  mit der imaginären Einheit  $\rm j$  ergibt, spielt für den Anwender keine Rolle.
• Die implizite Bedingung  $x(t) = 0$  für  $t < 0$  erlaubt speziell die einfachere Analyse des Einschwingverhaltens nach Einschaltvorgängen als mit dem Fourierintegral.

Definition der Laplace–Transformation

Ausgehend vom  ersten Fourierintegral,

$$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t,$$

ergibt sich bei kausaler Zeitfunktion   ⇒   $x(t) = 0 \ \ \text{für} \ \ t < 0$  mit der formalen Substitution  $p = {\rm j} · 2πf$  direkt die Laplace–Transformation:

$$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t} }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$

• Der Zusammenhang zwischen der Laplace–Transformierten  $X_{\rm L}(p)$  und dem physikalischen Spektrum  $X(f)$  ist häufig wie folgt gegeben:

$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$

$\text{Beispiel 1:}$  Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion  $x(t) ={\rm e}^{-t/T}$  für  $t > 0$  gemäß der Skizze  $\rm F$  in der unteren Tabelle aus.  Damit lautet die Laplace–Transformierte:

$$X_{\rm L}(p) = \int_{0}^{\infty} {\rm e}^{-t/T} \cdot {\rm e}^{-pt} \hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.08cm}\cdot \hspace{0.08cm}t}}\hspace{0.15cm}\Bigg \vert_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$

Mit  $p = {\rm j} · 2πf$  erhält man die herkömmliche Spektralfunktion bezüglich $f$:

$$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$

Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort  $h(t)$  sich gegenüber der obigen Zeitfunktion  $x(t)$  um den Faktor  $1/T$  unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte:

$$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT} } = \frac {1}{1+{\rm j} \cdot f/f_{\rm G} } \hspace{0.05cm} .$$

Häufig verwendet man dann wie in dieser Gleichung anstelle des Parameters  $T$  die 3dB–Grenzfrequenz  $f_{\rm G} = 1/(2πT)$.

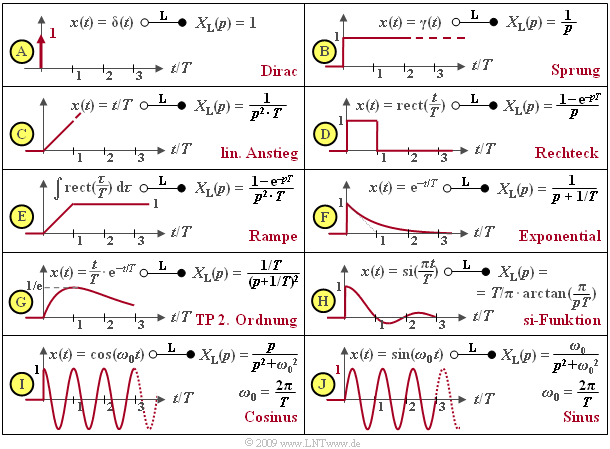
Einige wichtige Laplace–Korrespondenzen

Tabelle mit einigen Laplace-Transformierten

Hier sind einige wichtige Laplace–Korrespondenzen zusammengestellt.  Alle Zeitsignale  $x(t)$  seien dimensionslos.  Deshalb besitzt  $X_{\rm L}(p)$  dann als Integral über die Zeit stets die Einheit „Sekunde”.

• Die Laplace–Transformierte der  Diracfunktion  $δ(t)$  ist  $X_{\rm L}(p) = 1$  $($Diagramm $\rm A)$. 
• Durch Anwendung des  Integrationssatzes  erhält man  $X_{\rm L}(p) = 1/p$  für die Sprungfunktion  $γ(t)$  $($Diagramm $\rm B)$.
• Aus dieser wird durch Multiplikation mit  $1/(pT)$  die Laplace–Transformierte der linear ansteigenden Funktion  $x(t) = t/T$  für  $t > 0$  $($Diagramm $\rm C)$.

• Das  Rechteck  kann aus der Subtraktion zweier um  $T$  versetzter Sprungfunktionen  $γ(t)$  und  $γ(t – T)$  erzeugt werden. Mit dem  Verschiebungssatz:  $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$  ergibt  $($Diagramm $\rm D)$.
• Durch Integration erhält man die Rampe bzw. nach Multiplikation mit  $1/(pT)$  deren Laplace–Transformierte  $($Diagramm $\rm E)$.

• Die Exponentialfunktion  $($Diagramm $\rm F)$ wurde bereits im  $\text{Beispiel 1}$  betrachtet.  Mit dem Faktor  $1/T$  ist diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung.
• Durch Quadrierung erhält man die  $p$–Spektralfunktion eines Tiefpasses  $2.$ Ordnung und  $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm  $\rm G$).

• Neben der kausalen  $\rm si$–Funktion  $($Diagramm $\rm H)$  sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion  $($Diagramme  $\rm I$  und  $\rm J)$  angegeben, die sich zu  $p/(p^2 + ω_0^2)$  bzw.  $ω_0/(p^2 + ω_0^2)$  ergeben. Hierbei bezeichnet  $ω_0 = 2πf_0 = 2π/T$  die so genannte Kreisfrequenz.

Pol–Nullstellen–Darstellung von Schaltungen

Ein jedes  lineare zeitinvariante System  (LZI), das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie Widerständen  $(R)$,  Kapazitäten  $(C)$,  Induktivitäten  $(L)$  und Verstärkerelementen realisiert werden kann, besitzt eine gebrochen–rationale  $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{...} + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N +\text{...} \ + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

Alle Koeffizienten des Zählers   ⇒   $A_Z, \text{...} \ , A_0$  und des Nenners   ⇒   $B_N, \text{...} , B_0$  sind reell. Weiter bezeichnen mit

• $Z$  den Grad des Zählerpolynoms  $Z(p)$,
• $N$  den Grad des Nennerpolynoms  $N(p)$.

$\text{Äquivalente Pol–Nullstellen–Darstellung:}$   Für die  $p$–Übertragungsfunktion kann auch geschieben werden:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i} } {\prod\limits_{i=1}^N p - p_{\rm x i} }= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \ \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Die  $Z + N + 1$  Parameter bedeuten:

• $K = A_Z/B_N$  ist ein konstanter Faktor.   Gilt  $Z = N$, so ist dieser dimensionslos.
• Die Lösungen der Gleichung  $Z(p) = 0$  ergeben die  $Z$  Nullstellen  $p_{\rm o1},\text{...} \ , p_{\rm oZ}$  von  $H_{\rm L}(p)$.
• Die Nullstellen des Nennerpolynoms  $N(p)$  liefern die  $N$  Polstellen (oder kurz Pole).

Die Umformung ist eindeutig.  Dies erkennt man daran, dass die  $p$–Übertragungsfunktion gemäß der ersten Gleichung ebenfalls nur durch  $Z + N + 1$  freie Parameter bestimmt ist, da einer der Koeffizienten  $A_Z, \text{...} \ , A_0, B_N, \text{...} \ , B_0$  ohne Änderung des Quotienten auf  $1$  normiert werden kann.

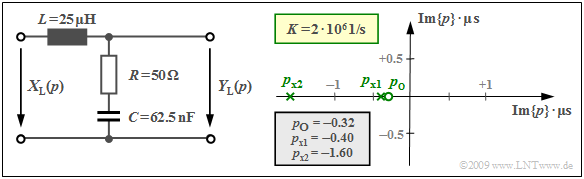
$\text{Beispiel 2:}$  Wir betrachten den gezeichneten Vierpol mit einer Induktivität  $L$  $($komplexer Widerstand  $pL)$  im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes  $R$  und einer Kapazität  $C$  mit dem komplexen Widerstand  $1/(pC)$.

Betrachteter Vierpol und dazugehöriges Pol–Nullstellen–Diagramm

Damit lautet die  $p$–Übertragungsfunktion  $H_{\rm L}(p)= {Y_{\rm L}(p)}/ {X_{\rm L}(p)}$:

$$H_{\rm L}(p)= \frac {R + {1}/{(pC)} } {pL + R +{1}/{(pC)} }= \frac {1 + p \cdot{RC} } {1 + p \cdot{RC}+ p^2 \cdot{LC} } \hspace{0.05cm} .$$

Dividiert man Zähler und Nenner durch  $LC$, so ergibt sich:

$$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)} } {p^2 + {R}/ {L}\cdot p + {1}/{(LC)} }$$

$$\Rightarrow \hspace{0.3cm}H_{\rm L}(p)= = K \cdot \frac {p - p_{\rm o } } {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$

Setzt man  $p = {\rm j} · 2πf$  ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang).

Im rechten Gleichungsteil ist die Übertragungsfunktion  $H_{\rm L}(p)$  in Pol–Nullstellen–Notation angegeben.  Durch Koeffizientenvergleich ergeben sich für  $R = 50 \ \rm Ω$,  $L = 25\ \rm µ H$  und  $C = 62.5 \ \rm nF$  folgende Werte:

• die Konstante  $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
• die Nullstelle  $p_{\rm o} = -1/(RC) = -0.32 · 10^6 \cdot 1/{\rm s},$
• die beiden Pole  $p_{\rm x1}$  und  $p_{\rm x2}$  als Lösung der Gleichung

$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$

In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben.

• Die beiden Achsen bezeichnen den Real– und den Imaginärteil der Variablen  $p$, jeweils normiert auf den Wert  $10^6 · \rm 1/s\; (= 1/µs)$.
• Man erkennt die Nullstelle bei  $p_{\rm o} =\, –0.32$  als Kreis und die Polstellen bei  $p_{\rm x1} = \,–0.4$  und  $p_{\rm x2} = \,–1.6$  als Kreuze.

Eigenschaften der Pole und Nullstellen

Die Übertragungsfunktion  $H_{\rm L}(p)$  einer jeden realisierbaren Schaltung wird durch  $Z$  Nullstellen und  $N$  Pole zusammen mit einer Konstanten  $K$  vollständig beschrieben, wobei folgende Einschränkungen gelten:

• Es gilt stets  $Z ≤ N$.  Mit  $Z > N$  wäre im Grenzfall für  $p → ∞$  (also für sehr hohe Frequenzen) auch die  $p$–Übertragungsfunktion „unendlich groß”.
• Die Nullstellen  $p_{\rm oi}$  und die Pole  $p_{ {\rm x}i}$  sind im allgemeinen komplex und weisen wie  $p$  die Einheit  $\rm 1/s$  auf. Gilt  $Z < N$, so besitzt auch die Konstante  $K$  eine Einheit.
• Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt.  Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da  $H_{\rm L}(p)$  stets eine reelle gebrochen–rationale Funktion darstellt.
• Alle Pole liegen in der linken Halbebene oder auf der imaginären Achse (Grenzfall). Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem  Hauptsatz der Funktionstheorie, der im nächsten Kapitel angegeben wird.
• Nullstellen können sowohl in der linken als auch in der rechten  $p$–Halbebene auftreten oder auch auf der imaginären Achse.  Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der  Aufgabe 3.4Z, die sich mit Allpässen beschäftigt.
• Bei den so genannten Minimum–Phasen–Systemen  sind in der rechten  $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen.  Der Realteil aller Singularitäten ist hier nie positiv.

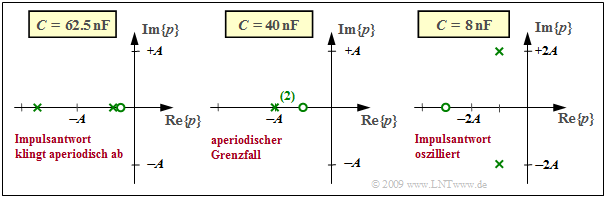
Diese Eigenschaften werden nun an drei Beispielen verdeutlicht.

$\text{Beispiel 3:}$  Ausgehend von der bereits im letzten Abschnitt betrachteten  Vierpolschaltung  $(L$  im Längszweig,  $R$  und  $C$  im Querzweig$)$  können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden:

$$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm mit } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC} } \hspace{0.05cm}.$$

Die Grafik zeigt drei verschiedene Diagramme mit unterschiedlichen Kapazitätswerten  $C$.  Es gilt stets  $R = 50 \ \rm Ω$  und  $L = 25 \ \rm µ H$.  Die Achsen sind auf die Variable  $A = R/(2L) = 10^6 · \rm 1/s$  normiert, und der konstante Faktor ist jeweils  $K = 2A = 2 · 10^6 · \rm 1/s.$

Lage der Nullstelle und der Pole für  $Z = 1$  und  $N = 2$

• Für  $B < A$  erhält man  zwei reelle Pole  und eine Nullstelle rechts von  $-A/2$.  Für  $C = 62.5 \ \rm nF$  ergibt sich (linkes Diagramm):

$${B}/ {A}= 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$

• Für  $B > A$  ergeben sich  zwei konjugiert–komplexe Pole  und eine Nullstelle links von  $-A/2$.  Für  $C = 8 \ \rm nF$  (rechtes Diagramm):

$${B}/ {A}= \sqrt{5} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$

• Der Fall  $A = B$  führt zu  einer reellen doppelten Polstelle  und einer Nullstelle bei  $– A/2$.  Für  $C = 400 \ \rm nF$  (mittleres Diagramm):

$${B}/ {A}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$

Die Impulsantworten  $h(t)$  ergeben sich entsprechend dem folgenden Kapitel  Laplace–Rücktransformation  wie folgt:

• Bei der linken Konstellation ist  $h(t)$  aperiodisch abklingend.
• Bei der rechten Konstellation ist  $h(t)$  gedämpft oszillierend.
• Bei der mittleren Konstellation spricht man vom  aperiodischen Grenzfall.

Grafische Ermittlung von Dämpfung und Phase

Gegeben sei die  $p$–Übertragungsfunktion in der Pol–Nullstellen–Notation:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Zum herkömmlichen Frequenzgang  $H(f)$  kommt man, indem man das Argument  $p$  von  $H_{\rm L}(p)$  durch  ${\rm j} \cdot 2πf$  ersetzt:

Ausgangsdiagramm zur Berechnung
von Dämpfung und Phase

$$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot \text{...} \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot \text{...}\cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

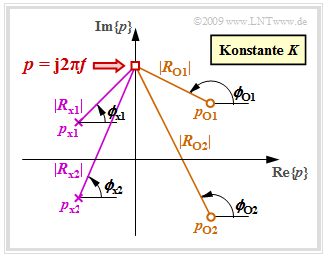
Wir betrachten nun eine feste Frequenz  $f$  und beschreiben die Abstände und Winkel aller Nullstellen durch Vektoren:

$$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm o} i} }, \hspace{0.3cm}i= 1, \text{...}\ , Z \hspace{0.05cm} .$$

In gleicher Weise gehen wir für die Polstellen vor:

$$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm x} i} }, \hspace{0.3cm}i= 1, \text{...}\ , N \hspace{0.05cm} .$$

Die Grafik zeigt die Beträge und Phasenwinkel für ein System

• mit  $Z = 2$  Nullstellen in der rechten Halbebene
• und  $N = 2$  Polstellen in der linken Halbebene.

Zu berücksichtigen ist zudem die Konstante  $K$.

Mit dieser Vektordarstellung kann für den Frequenzgang geschrieben werden:

$$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot \text{...} \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}\text{...}. \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$

Stellt man  $H(f)$  durch die Dämpfungsfunktion  $a(f)$  und die Phasenfunktion  $b(f)$  nach der allgemein gültigen Beziehung  $H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$  dar, so erhält man durch den Vergleich mit der obigen Gleichung das folgende Ergebnis:

• Bei geeigneter Normierung aller dimensionsbehafteten Größen gilt für die Dämpfung in Neper  $(1 \ \rm Np$ entspricht $8.686 \ \rm dB)$:

$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$

• Die Phasenfunktion in Radian $\rm (rad)$ ergibt sich entsprechend der oberen Skizze zu

$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm mit} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$

Zur Berechnung der Dämpfungs– und Phasenfunktion (Bildschirmabzug des Programms „Kausale Systeme & Laplace–Transformation” in einer früheren Version)

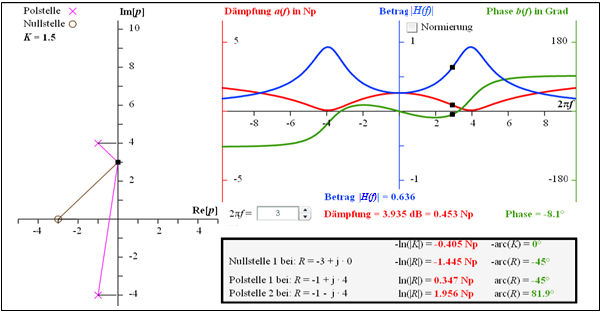
$\text{Beispiel 4:}$  Die Grafik verdeutlicht die Berechnung

• der Dämpfungsfunktion  $a(f)$   ⇒   roter Kurvenverlauf,  und
• der Phasenfunktion  $b(f)$   ⇒   grüner Kurvenverlauf

eines Vierpols, der durch den Faktor  $K = 1.5$, eine Nullstelle bei  $-3$  und zwei Pole bei  $–1 \pm {\rm j} · 4$  festliegt.

Die angegebenen Zahlenwerte gelten für die Frequenz  $2πf = 3$:

$$a \big [f = {3}/({2\pi}) \big ] = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB}$$

$$\Rightarrow \hspace{0.4cm}\big \vert H \big [f = {3}/({2\pi}) \big ]\big \vert = 0.636,$$

$$b\big [f = {3}/({2\pi}) \big ] = -8.1^\circ \hspace{0.05cm} .$$

Die Herleitung dieser Zahlenwerte ist im umrahmten Block verdeutlicht.

Für den Betragsfrequenzgang   $\vert H(f)\vert$   ⇒   blauer Kurvenverlauf ergibt sich ein bandpassähnlicher Verlauf mit

$$\vert H(f = 0)\vert \approx 0.25\hspace{0.05cm}, \hspace{0.5cm} \vert H(f = {4}/(2\pi)\vert \approx 0637\hspace{0.05cm},\hspace{0.5cm} \vert H(f \rightarrow \infty)\vert= 0 \hspace{0.05cm} .$$

Pol–Nullstellen–Darstellung von Schaltungen

Ein jedes  lineare zeitinvariante System  (LZI), das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie

• Widerständen  $(R)$,
• Kapazitäten  $(C)$,
• Induktivitäten  $(L)$  und
• Verstärkerelementen

realisiert werden kann, besitzt eine gebrochen–rationale  $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{...} + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N +\text{...} \ + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

Alle Koeffizienten des Zählers   ⇒   $A_Z, \text{...} \ , A_0$  und des Nenners   ⇒   $B_N, \text{...} , B_0$  sind reell. Weiter bezeichnen mit

• $Z$  den Grad des Zählerpolynoms  $Z(p)$,
• $N$  den Grad des Nennerpolynoms  $N(p)$.

$\text{Äquivalente Pol–Nullstellen–Darstellung:}$   Für die  $p$–Übertragungsfunktion kann auch geschieben werden:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i} } {\prod\limits_{i=1}^N p - p_{\rm x i} }= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \ \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Die  $Z + N + 1$  Parameter bedeuten:

• $K = A_Z/B_N$  ist ein konstanter Faktor.   Gilt  $Z = N$, so ist dieser dimensionslos.
• Die Lösungen der Gleichung  $Z(p) = 0$  ergeben die  $Z$  Nullstellen  $p_{\rm o1},\text{...} \ , p_{\rm oZ}$  von  $H_{\rm L}(p)$.
• Die Nullstellen des Nennerpolynoms  $N(p)$  liefern die  $N$  Polstellen (oder kurz Pole).

Die Umformung ist eindeutig.  Dies erkennt man daran, dass die  $p$–Übertragungsfunktion gemäß der ersten Gleichung ebenfalls nur durch  $Z + N + 1$  freie Parameter bestimmt ist, da einer der Koeffizienten  $A_Z, \text{...} \ , A_0, B_N, \text{...} \ , B_0$  ohne Änderung des Quotienten auf  $1$  normiert werden kann.

$\text{Beispiel 2:}$  Wir betrachten den gezeichneten Vierpol mit einer Induktivität  $L$  $($komplexer Widerstand  $pL)$  im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes  $R$  und einer Kapazität  $C$  mit dem komplexen Widerstand  $1/(pC)$.

Betrachteter Vierpol und dazugehöriges Pol–Nullstellen–Diagramm

Damit lautet die  $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)} } {pL + R +{1}/{(pC)} }= \frac {1 + p \cdot{RC} } {1 + p \cdot{RC}+ p^2 \cdot{LC} } \hspace{0.05cm} .$$

Setzt man  $p = {\rm j} · 2πf$  ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang). Dividiert man in obiger Gleichung Zähler und Nenner durch  $LC$, so ergibt sich:

$$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)} } {p^2 + {R}/ {L}\cdot p + {1}/{(LC)} }= K \cdot \frac {p - p_{\rm o } } {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$

Im rechten Gleichungsteil ist die Übertragungsfunktion  $H_{\rm L}(p)$  in Pol–Nullstellen–Notation angegeben.  Durch Koeffizientenvergleich ergeben sich für  $R = 50 \ \rm Ω$,  $L = 25\ \rm µ H$  und  $C = 62.5 \ \rm nF$  folgende Werte:

• die Konstante  $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
• die Nullstelle  $p_{\rm o} = -1/(RC) = -0.32 · 10^6 \cdot 1/{\rm s},$
• die beiden Pole  $p_{\rm x1}$  und  $p_{\rm x2}$  als Lösung der Gleichung

$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$

In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben.

• Die beiden Achsen bezeichnen den Real– und den Imaginärteil der Variablen  $p$, jeweils normiert auf den Wert  $10^6 · \rm 1/s\; (= 1/µs)$.
• Man erkennt die Nullstelle bei  $p_{\rm o} =\, –0.32$  als Kreis und die Polstellen bei  $p_{\rm x1} = \,–0.4$  und  $p_{\rm x2} = \,–1.6$  als Kreuze.

Eigenschaften der Pole und Nullstellen

Die Übertragungsfunktion  $H_{\rm L}(p)$  einer jeden realisierbaren Schaltung wird durch  $Z$  Nullstellen und  $N$  Pole zusammen mit einer Konstanten  $K$  vollständig beschrieben, wobei folgende Einschränkungen gelten:

• Es gilt stets  $Z ≤ N$.  Mit  $Z > N$  wäre im Grenzfall für  $p → ∞$  (also für sehr hohe Frequenzen) auch die  $p$–Übertragungsfunktion „unendlich groß”.
• Die Nullstellen  $p_{\rm oi}$  und die Pole  $p_{ {\rm x}i}$  sind im allgemeinen komplex und weisen wie  $p$  die Einheit  $\rm 1/s$  auf. Gilt  $Z < N$, so besitzt auch die Konstante  $K$  eine Einheit.
• Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt.  Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da  $H_{\rm L}(p)$  stets eine reelle gebrochen–rationale Funktion darstellt.
• Alle Pole liegen in der linken Halbebene oder auf der imaginären Achse (Grenzfall). Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem  Hauptsatz der Funktionstheorie, der im nächsten Kapitel angegeben wird.
• Nullstellen können sowohl in der linken als auch in der rechten  $p$–Halbebene auftreten oder auch auf der imaginären Achse.  Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der  Aufgabe 3.4Z, die sich mit Allpässen beschäftigt.
• Bei den so genannten Minimum–Phasen–Systemen  sind in der rechten  $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen.  Der Realteil aller Singularitäten ist hier nie positiv.

Diese Eigenschaften werden nun an drei Beispielen verdeutlicht.

{{GraueBox|TEXT= $\text{Beispiel 3:}$  Ausgehend von der bereits im letzten Abschnitt betrachteten  Vierpolschaltung  $(L$  im Längszweig,  $R$  und  $C$  im Querzweig$)$  können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden:

$$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm mit } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC} } \hspace{0.05cm}.$$

Die Grafik zeigt drei verschiedene Diagramme mit unterschiedlichen Kapazitätswerten  $C$.  Es gilt stets  $R = 50 \ \rm Ω$  und  $L = 25 \ \rm µ H$.  Die Achsen sind auf die Variable  $A = R/(2L) = 10^6 · \rm 1/s$  normiert, und der konstante Faktor ist jeweils  $K = 2A = 2 · 10^6 · \rm 1/s.$

Lage der Nullstelle und der Pole für  $Z = 1$  und  $N = 2$

• Für  $B < A$  erhält man  zwei reelle Pole  und eine Nullstelle rechts von  $-A/2$.  Für  $C = 62.5 \ \rm nF$  ergibt sich (linkes Diagramm):

$${B}/ {A}= 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$

• Für  $B > A$  ergeben sich  zwei konjugiert–komplexe Pole  und eine Nullstelle links von  $-A/2$.  Für  $C = 8 \ \rm nF$  (rechtes Diagramm):

$${B}/ {A}= \sqrt{5} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$

• Der Fall  $A = B$  führt zu  einer reellen doppelten Polstelle  und einer Nullstelle bei  $– A/2$.  Für  $C = 400 \ \rm nF$  (mittleres Diagramm):

$${B}/ {A}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$

Frequenzgang  $H(f)$  und Impulsantwort  $h(t)$

• Der  Frequenzgang  (oder auch die  Übertragungsfunktion)  $H(f)$  eines linearen zeitinvarianten Übertragungssystems gibt das Verhältnis zwischen dem Ausgangsspektrum  $Y(f)$  und dem dem Eingangsspektrum  $X(f)$  an:

$$H(f) = \frac{Y(f)}{X(f)}.$$

• Ist das Übertragungsverhalten bei tiefen Frequenzen besser als bei höheren, so spricht man von einem  Tiefpass  (englisch:  Low-pass).
• Die Eigenschaften von  $H(f)$  werden im Zeitbereich durch die  Impulsantwort  $h(t)$  ausgedrückt.  Entsprechend dem  zweiten Fourierintegral  gilt:

$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$

• Die Gegenrichtung wird durch das  erste Fourierintegral  beschrieben:

$$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$

• In allen Beispielen verwenden wir reelle und gerade Funktionen.  Somit gilt:

$$h(t)=\int_{-\infty}^{+\infty}H(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H(f)=\int_{-\infty}^{+\infty}h(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$

• Bei einem Vierpol  $[$das bedeutet:  $X(f)$  und  $Y(f)$  haben gleiche Einheiten$]$   ist  $Y(f)$  dimensionslos. 
• Die Einheit der Impulsantwort ist  $\rm 1/s$.  Es gilt zwar $\rm 1/s = 1 \ Hz$, aber die Einheit „Hertz” ist in diesem Zusammenhang unüblich.
• Der Zusammenhang zwischen diesem Applet und dem ähnlich aufgebauten Applet  Impulse und Spektren  basiert auf dem  Vertauschungssatz.
• Alle Zeiten sind auf eine Normierungszeit  $T$  normiert und alle Frequenzen auf  $1/T  \ \Rightarrow$  die Zahlenwerte von   $h(t)$  müssen noch durch  $T$  dividiert werden.

$\text{Beispiel:}$  Stellt man einen Rechteck–Tiefpass mit Höhe  $K_1 = 1$  und äquivalenter Bandbreite  $\Delta f_1 = 1$  ein,

• so ist der Frequenzgang  $H_1(f)$  im Bereich  $-1 < f < 1$  gleich  $1$  und außerhalb dieses Bereichs gleich Null. 
• Die Impulsantwort  $h_1(t)$  verläuft  $\rm si$–förmig mit  $h_1(t= 0) = 1$  und der ersten Nullstelle bei  $t=1$.

Mit dieser Einstellung soll nun ein Rechteck–Tiefpass mit  $K = 1.5$  und  $\Delta f = 2 \ \rm kHz$  nachgebildet werden, wobei die Normierungszeit  $T= 1 \ \rm ms$  betrage. 

• Dann liegt die erste Nullstelle bei  $t=0.5\ \rm ms$  und das Impulsantwortmaximum ist dann  $h(t= 0) = 3 \cdot 10^3 \ \rm 1/s$.

Gauß–Tiefpass   $\Rightarrow$   Gaussian Low–pass

• Der Gauß–Tiefpass lautet mit der Höhe  $K$  und der (äquivalenten) Bandbreite  $\Delta f$:

$$H(f)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f/\Delta f)^2}.$$

• Die äquivalente Bandbreite  $\Delta f$  ergibt sich aus dem flächengleichen Rechteck.
• Der Wert bei  $f = \Delta f/2$  ist um den Faktor  $0.456$  kleiner als der Wert bei  $f=0$.
• Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:

$$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f)^2} .$$

• Je kleiner  $\Delta f$  ist, um so breiter und niedriger ist die Impulsantwort   ⇒   Reziprozitätsgesetz von Bandbreite und Impulsdauer.
• Sowohl  $H(f)$  als auch  $h(t)$  sind zu keinem  $f$– bzw.  $t$–Wert exakt gleich Null.
• Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. 
• Zum Beispiel ist  $h(t)$  bereits bei  $t=1.5 \cdot \Delta t$  auf weniger als  $0.1\%$  des Maximums abgefallen.

Idealer (rechteckförmiger) Tiefpass   $\Rightarrow$   Rectangular Low–pass

• Der Rechteck–Tiefpass lautet mit der Höhe  $K$  und der (äquivalenten) Bandbreite  $\Delta f$:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$

• Der  $\pm \Delta f/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
• Für die Impulsantwort  $h(t)$  erhält man entsprechend den Gesetzmäßigkeiten der Fourierrücktransformation (2. Fourierintegral):

$$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t) \quad \text{mit} \quad {\rm si}(x)={\sin(x)}/{x}.$$

• Der  $h(t)$–Wert bei  $t=0$  ist gleich der Rechteckfläche des Frequenzgangs.
• Die Impulsantwort besitzt Nullstellen in äquidistanten Abständen  $1/\Delta f$.
• Das Integral über die Impulsantwort  $h(t)$  ist gleich dem Frequenzgang  $H(f)$  bei der Frequenz  $f=0$, ist also gleich  $K$.

Dreieck–Tiefpass   $\Rightarrow$   Triangular Low–pass

• Der Dreieck–Tiefpass lautet mit der Höhe  $K$  und der (äquivalenten) Bandbreite  $\Delta f$:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$

• Die absolute physikalische Bandbreite  $B$   ⇒   [nur positive Frequenzen]   ist ebenfalls gleich  $\Delta f$, ist also so groß wie beim Rechteck–Tiefpass.
• Für die Impulsantwort  $h(t)$  erhält man gemäß der Fouriertransformation:

$$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{mit} \quad {\rm si}(x)={\sin(x)}/{x}.$$

• $H(f)$  kann man als Faltung zweier Rechteckfunktionen  $($jeweils mit Breite  $\Delta f)$  darstellen.
• Daraus folgt:  $h(t)$  beinhaltet anstelle der  ${\rm si}$-Funktion die  ${\rm si}^2$-Funktion.
• $h(t)$  weist somit ebenfalls Nullstellen im äquidistanten Abständen  $1/\Delta f$  auf.
• Der asymptotische Abfall von  $h(t)$  erfolgt hier mit  $1/t^2$, während zum Vergleich beim Rechteck–Tiefpass  $h(t)$  mit  $1/t$  abfällt.

Trapez–Tiefpass   $\Rightarrow$   Trapezoidal Low–pass

Der Trapez–Tiefpass lautet mit der Höhe  $K$  und den beiden Eckfrequenzen  $f_1$  und  $f_2$:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$

• Für die äquivalente Bandbreite  (flächengleiches Rechteck)  gilt:  $\Delta f = f_1+f_2$.
• Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{f_2-f_1}{f_2+f_1}.$$

• Der Sonderfall  $r=0$  entspricht dem Rechteck–Tiefpass und der Sonderfall  $r=1$  dem Dreieck–Tiefpass.
• Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:

$$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t)\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t) \quad \text{mit} \quad {\rm si}(x)={\sin(x)}/{x}.$$

• Der asymptotische Abfall von  $h(t)$  liegt zwischen  $1/t$  $($für Rechteck–Tiefpass oder  $r=0)$  und  $1/t^2$  $($für Dreieck–Tiefpass oder  $r=1)$.

Cosinus-Rolloff-Tiefpass   $\Rightarrow$   Cosine-rolloff Low–pass

Der Cosinus–Rolloff–Tiefpass lautet mit der Höhe  $K$  und den beiden Eckfrequenzen  $f_1$  und  $f_2$:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$

• Für die äquivalente Bandbreite  (flächengleiches Rechteck)  gilt:  $\Delta f = f_1+f_2$.
• Der Rolloff-Faktor (im Frequenzbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{f_2-f_1}{f_2+f_1}.$$

• Der Sonderfall  $r=0$  entspricht dem Rechteck–Tiefpass und der Sonderfall  $r=1$  dem Cosinus-Quadrat-Tiefpass.
• Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:

$$h(t)=K\cdot \Delta f \cdot \frac{\cos(\pi \cdot r\cdot \Delta f \cdot t)}{1-(2\cdot r\cdot \Delta f \cdot t)^2} \cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$

• Je größer der Rolloff-Faktor  $r$  ist, desto schneller nimmt  $h(t)$  asymptotisch mit  $t$  ab.

Cosinus-Quadrat-Tiefpass   $\Rightarrow$   Cosine-rolloff -squared Low–pass

• Dies ist ein Sonderfall des Cosinus–Rolloff–Tiefpasses und ergibt sich aus diesem für  $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}f_1=0,\ f_2= \Delta f$:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$

• Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:

$$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm si}(\pi(\Delta f\cdot t +0.5))+{\rm si}(\pi(\Delta f\cdot t -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$

• Wegen der letzten  ${\rm si}$-Funktion ist  $h(t)=0$  für alle Vielfachen von  $T=1/\Delta f$   ⇒   Die äquidistanten Nulldurchgänge des Cosinus–Rolloff–Tiefpasses bleiben erhalten.
• Aufgrund des Klammerausdrucks weist  $h(t)$  nun weitere Nulldurchgänge bei  $t=\pm1.5 T$,  $\pm2.5 T$,  $\pm3.5 T$, ...  auf.
• Für  $t=\pm T/2$  hat die Impulsanwort den Wert  $K\cdot \Delta f/2$.
• Der asymptotische Abfall von  $h(t)$  verläuft in diesem Sonderfall mit  $1/t^3$.

Versuchsdurchführung

• Wählen Sie zunächst die Nummer  $(1,\ 2$, ... $)$  der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt.  Die Parameterwerte sind angepasst.
• Lösung nach Drücken von „Musterlösung”.
• Die Nummer  $0$  entspricht einem „Reset”:  Einstellung wie beim Programmstart.
• „Rot” bezieht sich auf den ersten Parametersatz   ⇒   $H_1(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_1(t)$.
• „Blau” bezieht sich auf den zweiten Parametersatz   ⇒   $H_2(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_2(t)$.
• Werte betragsmäßig kleiner  $0.0005$  werden im Programm zu Null gesetzt.
  

(1)   Vergleichen Sie den  roten Gauß–Tiefpass  $(K_1 = 1, \ \Delta f_1 = 1)$  mit dem  blauen Rechteck–Tiefpass  $(K_2 = 1,\ \Delta f_2 = 1)$.  Fragen:
          (a)  Welche Ausgangssignale  $y(t)$  ergeben sich, wenn am Eingang das Signal  $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$  mit  $f_0 = 0.5$  anliegt?
          (b)  Welche Unterschiede ergeben sich bei beiden Tiefpässen mit  $f_0 = 0.5 \pm f_\varepsilon$  und  $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$?

(a)  Es gilt  $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$  mit  $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 0.912, \ A_2 = 1.000$.  Die Phase  $\varphi_0$  bleibt erhalten.

(b)  Bei  Rot  gilt weiterhin  $A_1 = 0.912$.  Bei  Blau  ist  $A_2 = 0$  für  $f_0 = 0.5000\text{...}001$  und  $A_2 = 2$  für  $f_0 = 0.4999\text{...}999$.

(2)   Lassen Sie die Einstellungen unverändert.  Welcher Tiefpass  $H(f)$  kann das erste oder das zweite Nyquistkriterium erfüllen?
        Hierbei bezeichnet  $H(f)$  den Gesamtfrequenzgang von Sender, Kanal und Empfangsfilter.

• Erstes Nyquistkriterium:  Die Impulsantwort  $h(t)$  muss äquidistante Nulldurchgänge zu den (normierten) Zeiten  $t = 1,\ 2$, ...  aufweisen.
• Die Impulsantwort  $h(t) = {\rm si}(\pi \cdot \Delta f \cdot t)$  des Rechteck–Tiefpasses erfüllt dieses Kriterium mit  $\Delta f = 1$.
• Dagegen wird beim Gauß–Tiefpass das erste Nyquistkriterium nie erfüllt und es kommt immer zu Impulsinterferenzen.
• Das zweite Nyquistkriterium erfüllt weder der Rechteck–Tiefpass noch der Gauß–Tiefpass.

(3)   Vergleichen Sie den  roten Rechteck–Tiefpass  $(K_1 = 0.5, \ \Delta f_1 = 2)$  mit dem  blauen Rechteck–Tiefpass  $(K_2 = 1, \ \Delta f_2 = 1)$.
        Variieren Sie anschließend  $\Delta f_1$  zwischen  $2$  und  $0.5$.

• Mit  $\Delta f_1 = 2$  liegen die Nullstellen von  $h_1(t)$  bei Vielfachen von  $0.5$   ⇒   $h_1(t)$  klingt doppelt so schnell ab wie  $h_2(t)$.
• Mit der vorliegenden Einstellung gilt  $h_1(t = 0) = h_2(t = 0)$, da die Rechteckflächen von  $H_1(f)$  und  $H_2(f)$  gleich sind.
• Verringert man man  $\Delta f_1$, so wird die Impulsantwort  $h_1(t)$  immer breiter und niedriger.
• Mit  $\Delta f_1 = 0.5$  ist  $h_1(t)$  doppelt so breit wie  $h_2(t)$, gleichzeitig aber um den Faktor  $4$  niedriger.

(4)   Vergleichen Sie den  roten Trapez–Tiefpass  $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$  mit dem  blauen Rechteck–Tiefpass  $(K_2 = 1, \ \Delta f_2 = 1)$.
        Variieren Sie anschließend  $r_1$  zwischen  $0$  und  $1$.

• Mit  $r_1 = 0.5$  sind die Unterschwinger von  $h_1(t)$  beim „Trapez” wegen des flacheren Flankenabfalls geringer als beim „Rechteck”.
• Mit kleinerem  $r_1$  nehmen die Unterschwinger zu.  Mit  $r_1= 0$  ist der Trapez– gleich dem Rechteck–Tiefpass   ⇒   $h(t)= {\rm si}(\pi \cdot t/T)$.
• Mit größerem  $r_1$  werden die Unterschwinger kleiner. Mit  $r_1= 1$  ist der Trapez– gleich dem Dreieck–Tiefpass   ⇒   $h(t)= {\rm si}^2(\pi \cdot t/T)$.

(5)   Vergleichen Sie den  Trapez–Tiefpass  $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$  mit dem  Cosinus-Rolloff-Tiefpass  $(K_2 = 1,\ \Delta f_2 = 1, \ r_2 = 0.5)$.
        Variieren Sie  $r_2$  zwischen  $0$  und  $1$.  Interpretieren Sie die Impulsantwort für  $r_2 = 0.75$.  Welcher Tiefpass erfüllt das erste Nyquistkriterium?

• Bei  $r_1 = r_2= 0.5$  verläuft der Flankenabfall von  $H_2(f)$  um die Frequenz  $f = 0.5$  steiler als der Flankenabfall von  $H_1(f)$.
• Bei gleichem Rolloff  $r= 0.5$  hat die Impulsantwort  $h_2(t)$  für  $t > 1$  betragsmäßig größere Anteile als  $h_1(t)$.
• Mit  $r_1 = 0.5$  und  $r_2 = 0.75$  gilt  $H_1(f) \approx H_2(f)$  und damit auch  $h_1(t) \approx h_2(t)$.
• $H_1(f)$  und  $H_2(f)$  erfüllen beide das erste Nyquistkriterium:  Beide Funktionen sind punktsymmetrisch um den „Nyquistpunkt”.
• Wegen  $\Delta f = 1$  besitzen sowohl  $h_1(t)$  als auch  $h_2(t)$  Nulldurchgänge bei  $\pm 1$,  $\pm 2$, ...   ⇒   jeweils maximale vertikale Augenöffnung.

(6)   Vergleichen Sie den  Cosinus–Quadrat–Tiefpass  $(K_1 = 1, \ \Delta f_1 = 1)$  mit dem  Cosinus-Rolloff-Tiefpass  $(K_2 = 1, \ \Delta f_2 = 1,\ r_2 = 0.5)$.
        Variieren Sie  $r_2$  zwischen  $0$  und  $1$.  Interpretieren Sie die Ergebnisse.  Welcher Tiefpass erfüllt das zweite Nyquistkriterium]]?

• $H_1(f)$  ist ein Sonderfall des Cosinus–Rolloff–Tiefpasses mit Rolloff  $r_2 =1$.  Das erste Nyquistkriterium wird auch mit  $r_2 \ne 1$  erfüllt.
• Nach dem zweiten Nyquistkriterium muss  $h(t)$  auch Nulldurchgänge bei  $t=\pm 1.5$,  $\pm 2.5$,  $\pm 3.5$, ... besitzen  $($nicht jedoch bei  $t = \pm 0.5)$.
• Für den Cosinus–Quadrat–TP gilt also  $h_1(t=\pm 0.5) = 0.5$,  $h_1(t=\pm 1) = h_1(t=\pm 1.5) = h_1(t=\pm 2)= h_1(t=\pm 2.5) = \text{...} =0$.
• Nur der Cosinus–Quadrat–TP erfüllt das erste und zweite Nyquistkriterium gleichzeitig:  Maximale vertikale und horizontale Augenöffnung.

Zur Handhabung des Programms

Bildschirmabzug (englische Version, heller Hintergrund)

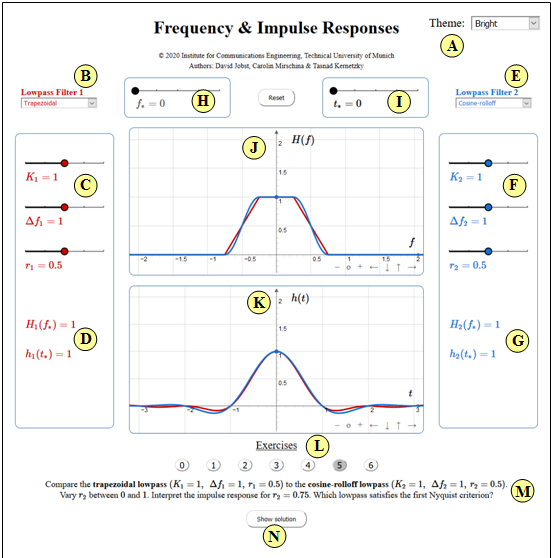
    (A)     Theme (veränderbare grafische Oberflächengestaltung)

• Dark:   schwarzer Hintergrund  (wird von den Autoren empfohlen)
• Bright:   weißer Hintergrund  (empfohlen für Beamer und Ausdrucke)
• Deuteranopia:   für Nutzer mit ausgeprägter Grün–Sehschwäche
• Protanopia:   für Nutzer mit ausgeprägter Rot–Sehschwäche

    (B)     Vorauswahl für den Frequenzgang  $H_1(f)$  (rote Kurve)

    (C)     Parameterfestlegung für  $H_1(f)$ 

    (D)     Numerikausgabe für  $H_1(f_*)$  und  $h_1(t_*)$

    (E)     Vorauswahl für den Frequenzgang  $H_2(f)$  (blaue Kurve)

    (F)     Parameterfestlegung für  $H_2(f)$ 

    (G)     Numerikausgabe für  $H_2(f_*)$  und  $h_2(t_*)$

    (H)     Einstellung der Frequenz  $f_*$  für die Numerikausgabe

    (I)      Einstellung der Zeit  $t_*$  für die Numerikausgabe

    (J)     Bereich der graphischen Darstellung im Frequenzbereich

    (K)     Bereich der graphischen Darstellung im Zeitbereich

    (L)     Auswahl der Aufgabe entsprechend der Aufgabennummer

    (M)     Aufgabenbeschreibung und Fragestellung

    (N)     Musterlösung anzeigen und verbergen

Details zu den obigen Punkten  (J ) und  (K)

Zoom–Funktionen:
       „$+$” (Vergrößern),      „$-$” (Verkleinern),      „$\rm o$” (Zurücksetzen)

Verschiebe–Funktionen:     „$\leftarrow$”     „$\uparrow$”     „$\downarrow$”     „$\rightarrow$”
        „$\leftarrow$”  bedeutet:     Bildausschnitt nach links, Ordinate nach rechts

Andere Möglichkeiten:

• Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
• Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
• 2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen       English Version