Periodendauer periodischer Signale

Wir bieten hier zwei Applets zur gleichen Thematik mit unterschiedlichem Layout an:

Applet-Variante 1 in neuem Tab öffnen     Applet-Variante 2 in neuem Tab öffnen

Programmbeschreibung

Dieses Applet zeichnet den Verlauf und berechnet die Periodendauer  $T_0$  der periodischen Funktion

$$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$

Bitte beachten Sie:

• Die Phasen  $\varphi_i$  sind hier im Bogenmaß einzusetzen.  Umrechnung aus dem Eingabewert:  

$$\varphi_i \text{[im Bogenmaß]} =\varphi_i \text{[in Grad]}/360 \cdot 2\pi.$$

• Ausgegeben werden auch der Maximalwert  $x_{\rm max}$  und ein Signalwert  $x(t_*)$  zu einer vorgebbaren Zeit  $t_*$.
• Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung.

Die englische Beschreibung finden Sie unter Period Duration of Periodic Signals.

Theoretischer Hintergrund

Ein periodisches Signal  $x(t)$  liegt genau dann vor, wenn dieses nicht konstant ist und für alle beliebigen Werte von  $t$  und alle ganzzahligen Werte von  $i$  mit einem geeigneten  $T_{0}$  gilt:   $x(t+i\cdot T_{0}) = x(t).$

• Man bezeichnet  $T_0$  als die  Periodendauer  und  $f_0 = 1/T_0$  als die  Grundfrequenz.

• Bei einer harmonischen Schwingung  $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$  gilt  $f_0 = f_1$  und  $T_0 = 1/f_1$,  unabhängig von der Phase  $\varphi_1$  und der Amplitude  $A_1 \ne 0$.

$\text{Berechnungsvorschrift:}$  Setzt sich das periodisches Signal  $x(t)$  wie in diesem Applet aus zwei Anteilen  $x_1(t)$  und  $x_2(t)$  zusammen, dann gilt mit  $A_1 \ne 0$,  $f_1 \ne 0$,  $A_2 \ne 0$,  $f_2 \ne 0$  für Grundfrequenz und Periodendauer:

$$f_0 = {\rm ggT}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0.$$

Hierbei bezeichnet  $\rm ggT$  den größten gemeinsamen Teiler.

$\text{Beispiele:}$   Im Folgenden bezeichnen  $f_0'$,  $f_1'$  und $f_2'$  jeweils auf $1\ \rm kHz$ normierte Signalfrequenzen:

(a)   $f_1' = 1.0$,   $f_2' = 3.0$   ⇒   $f_0' = {\rm ggt}(1.0, \ 3.0) = 1.0$   ⇒   $T_0 = 1.0\ \rm ms$;

(b)   $f_1' = 1.0$,   $f_2' = 3.5$   ⇒   $f_0' = {\rm ggt}(1.0, \ 3.5)= 0.5$   ⇒   $T_0 = 2.0\ \rm ms$;

(c)   $f_1' = 1.0$,   $f_2' = 2.5$   ⇒   $f_0' = {\rm ggt}(1.0, \ 2.5) = 0.5$   ⇒   $T_0 = 2.0\ \rm ms$;

(d)   $f_1' = 0.9$,   $f_2' = 2.5$   ⇒   $f_0' = {\rm ggt}(0.9, \ 2.5) = 0.1$   ⇒   $T_0 = 10.0 \ \rm ms$;

(e)   $f_2' = \sqrt{2} \cdot f_1'$   ⇒   $f_0' = {\rm ggt}(f_1', \ f_2') \to 0$   ⇒   $T_0 \to \infty$  ⇒   Das Signal  $x(t)$  ist nicht periodisch.

$\text{Anmerkung:}$  Die Periodendauer könnte auch als  kleinstes gemeinsames Vielfaches  $\rm (kgV)$  entsprechend  $T_0 = {\rm kgV}(T_1, \ T_2)$  ermittelt werden:

(c)   $T_1 = 1.0\ \rm ms$,   $T_2 = 0.4\ \rm kHz$   ⇒   $T_0 = {\rm kgV}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$

Bei allen anderen Parameterwerten würde es aber zu numerischen Problemen kommen, zum Beispiel

(a)   $T_1 = 1.0\ \rm ms$ und $T_2 = 0.333\text{...} \ \rm ms$ besitzen aufgrund der begrenzten Darstellung reeller Zahlen kein kleinstes gemeinsames Vielfaches.

Versuchsdurchführung

• Wählen Sie zunächst die Nummer  $(1,\ 2$, ... $)$  der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt.  Parameterwerte sind angepasst.
• Lösung nach Drücken von „Musterlösung”.
• Die Nummer  $0$  entspricht „Reset”:  Einstellung wie beim Programmstart.
• $A_1'$  und  $A_2'$  bezeichnen hier die auf  $1\ \rm V$  normierten Signalamplituden.
• $f_0'$,  $f_1'$  und  $f_2'$  sind die auf  $1\ \rm kHz$  normierten Frequenzen.

(1)   Es gelte  $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 2.0, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$  Wie groß ist die Periodendauer  $T_0$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist  $T_0 = 2.0 \ \rm ms$  wegen  ${\rm ggt}(2.0, 2.5) = 0.5$.

(2)   Variieren Sie  $\varphi_1$  und  $\varphi_2$  im gesamten möglichen Bereich $\pm 180^\circ\text{.}$  Wie wirkt sich dies auf die Periodendauer  $T_0$  aus?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer  $T_0 = 2.0 \ \rm ms$  bleibt für alle  $\varphi_1$  und  $\varphi_2$  erhalten.

(3)   Wählen Sie die Voreinstellung   ⇒   „Recall Parameters”.  Variieren Sie  $A_1'$  im gesamten möglichen Bereich  $0 \le A_1' \le 1$.

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer  $T_0 = 2.0 \ \rm ms$  bleibt erhalten mit Ausnahme von  $A_1' =0$.  In letzerem Fall ist  $T_0 = 0.4 \ \rm ms$.

(4)   Wählen Sie die Voreinstellung   ⇒   „Recall Parameters” und variieren Sie  $f_2'$?  Hat dies Auswirkungen auf  $T_0$?  Welcher Wert ergibt sich für  $f_2' = 0.2$.

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer springt hin und her.  Für  $f_2' = 0.2$  ergibt sich  $T_0 = 5.0 \ \rm ms$   wegen   ${\rm ggt}(2.0, 0.2) = 0.2$.

(5)   Es gelte  $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 0.2, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$  Wie groß ist  $T_0$?  Speichern Sie diese Einstellung mit „Store Parameters”.

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist  $T_0 = 10.0 \ \rm ms$  wegen  ${\rm ggt}(0.2, 2.5) = 0.1$.

(6)   Wählen Sie die letzte Einstellung   ⇒   „Recall Parameters” und ändern Sie  $f_2' = 0.6$.  Speichern Sie diese Einstellung mit „Store Parameters”:

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist  $T_0 = 5.0 \ \rm ms$  wegen  ${\rm ggt}(0.2,0.6) = 0.2$.

(7)   Wie groß ist bei gleicher Einstellung der maximale Signalwert  $x_{\rm max}\text{?}$

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.38 \ {\rm V} < A_1 + A_2$  mit  $t_* = 0.3 \ \rm ms$  und  $T_0 = 5.0 \ \rm ms$.

(8)   Welcher Unterschied ergibt sich mit  $\varphi_2 = 0^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Cosinusschwingungen?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $t_* = 0$,  $T_0 = 5.0 \ \rm ms$  ⇒   $x_{\rm max} =x(t_* + i \cdot T_0) = 1.5 \ {\rm V}=A_1 + A_2$.

(9)   Nun gelte  $\varphi_1 = \varphi_2 = 90^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Sinusschwingungen.  Wie groß ist hier der maximale Signalwert  $x_{\rm max}\text{?}$

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist nun  $x_{\rm max} = 1.07 \ {\rm V} < A_1 + A_2$. Dieser Wert ergibt sich mit  $T_0 = 5.0 \ \rm ms$  sowie  $t_* = 0.6 \ \rm ms$  bzw.  $t_* = 1.9 \ \rm ms$.

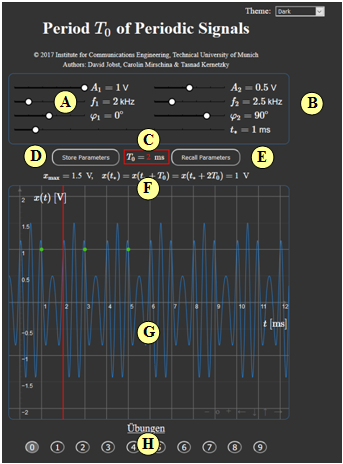
Zur Handhabung der Applet-Variante 1

    (A)     Parametereingabe per Slider

    (B)     Bereich der graphischen Darstellung

    (C)     Variationsmöglichkeit für die graphische Darstellung

    (D)     Abspeichern und Zurückholen von Parametersätzen

    (E)     Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie

    (F)     Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$

    (G)     Darstellung der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ durch grüne Punkte

    (H)     Einstellung der Zeit $t_*$ für die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$

Details zum obigen Punkt (C)

    (*)   Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)

    (*)   Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”

Andere Möglichkeiten:

    (*)   Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,

    (*)   Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am  Lehrstuhl für Nachrichtentechnik  der  Technischen Universität München  konzipiert und realisiert.

• Die erste Version wurde 2004 von  Ji Li  im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt  (Betreuer:  Günter Söder ).
• 2017 wurde dieses Programm von  David Jobst  im Rahmen seiner Ingenieurspraxis  (Betreuer:  Tasnád Kernetzky)  auf „HTML5” umgesetzt und neu gestaltet   ⇒   Applet-Variante 1.  Parallel dazu erarbeitete  Bastian Siebenwirth  im Rahmen seiner Bachelorarbeit  (Betreuer:  Günter Söder)  die HTML5-Variante 2.

Nochmalige Aufrufmöglichkeit der Applets in neuem Fenster

Wir bieten hier zwei Applets zur gleichen Thematik mit unterschiedlichem Layout an:

Applet-Variante 1 in neuem Tab öffnen     Applet-Variante 2 in neuem Tab öffnen