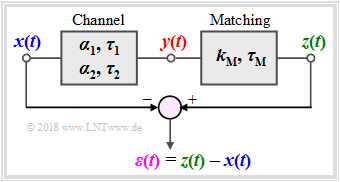
Linear Distortions of Periodic Signals

Open Applet in new Tab

Applet Description

This applet illustrates the effects of linear distortions (attenuation distortions and phase distortions) with

Meanings of the used signals

• the input signal $x(t)$   ⇒   power $P_x$:

$$x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right),$$

• the output signal $y(t)$   ⇒   power $P_y$:

$$y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2),$$

• the matched output signal $z(t)$   ⇒   power $P_z$:

$$z(t) = k_{\rm M} \cdot y(t-\tau_{\rm M}) + \alpha_2 \cdot x_2(t-\tau_2),$$

• the difference signal   $\varepsilon(t) = z(t) - x(t)$   ⇒   power $P_\varepsilon$.

The next block in the model above is Matching: The output signal $y(t)$ is adjusted in amplitude and phase with equal quantities $k_{\rm M}$ and $\tau_{\rm M}$ for all frequencies which means that this is not a frequency-dependent equalization. Using the signal $z(t)$, one can differentiate between:

• attenuation distortion and frequency–independant attenuation, as well as
• phase distortion and frequency–independant delay.

The Distortion Power $P_{\rm D}$ is used to measure the strength of the linear distortion and is defined as:

$$P_{\rm D} = \min_{k_{\rm M}, \ \tau_{\rm M}} P_\varepsilon.$$

German description

Theoretical Background

Distortions refer to generally unwanted alterations of a message signal through a transmission system. Together with the strong stochastic effects (noise, crosstalk, etc.), they are a crucial limitation for the quality and rate of transmission.

Just as the intensity of noise can be assessed through

• the Noise Power $P_{\rm N}$ and
• the Signal–to–Noise Ratio (SNR) $\rho_{\rm N}$,

distortions can be quantified through

• the Distortion Power $P_{\rm D}$ and
• the Signal–to–Distortion Ratio (SDR)

$$\rho_{\rm D}=\frac{\rm Signal \ Power}{\rm Distortion \ Power} = \frac{P_x}{P_{\rm D} }.$$

Linear and Nonlinear Distortions

A distinction is made between linear and nonlinear distortions:

• Nonlinear distortions occur, if at all times $t$ the nonlinear correlation $y = g(x) \ne {\rm const.} \cdot x$ exists between the signal values $x = x(t)$ at the input and $y = y(t)$ at the output, whereby $y = g(x)$ is defined as the system's nonlinear characteristic. By creating a cosine signal at the input with frequency $f_0$ the output signal includes $f_0$, as well as multiple harmonic waves. We conclude that new frequencies arise through nonlinear distortion.

For clarification of nonlinear distortions

Description of a linear system

• Linear distortions occur, if the transmission channel is characterized by a frequency response $H(f) \ne \rm const.$ Various frequencies are attenuated and delayed differently. Characteristic of this is that although frequencies can disappear (for example, through a low–pass, a high–pass, or a band–pass), no new frequencies can arise.

In this applet only linear distortions are considered.

Description Forms for the Frequency Response

The generally complex valued frequency response can be represented as follows:

$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$

This results in the following description variables:

• The absolute value $|H(f)|$ is called amplitude response and in logarithmic form attenuation function:

$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Decibel \hspace{0.1cm}(dB) }.$$

• The phase function $b(f)$ indicates the negative frequency–dependent angle of $H(f)$ in the complex plane based on the real axis:

$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$

Low–pass of Order N

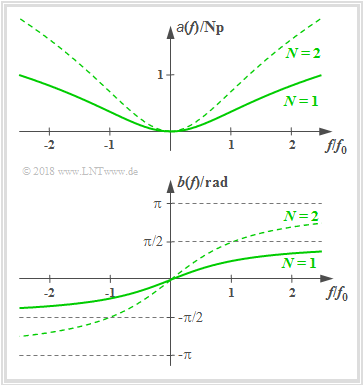
Attenuation function $a(f)$ and phase function $b(f)$ of a low–Pass of order $N$

The frequency response of a realizable low–pass (LP) of order $N$ is:

$$H(f) = \left [\frac{1}{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$

For example the RC low–pass is a first order low–pass. Consequently we can obtain

• the attenuation function:

$$a(f) =N/2 \cdot \ln [1+( f/f_0)^2] \hspace{0.05cm},$$

• the phase function:

$$b(f) =N \cdot \arctan( f/f_0) \hspace{0.05cm},$$

• the attenuation factor for the frequency $f=f_i$:

$$\alpha_i =|H(f = f_i)| = [1+( f_i/f_0)^2]^{-N/2}$$

$$\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$

• the phase delay for the frequency $f=f_i$:

$$\tau_i =\frac{b(f_i)}{2 \pi f_i} = \frac{N \cdot \arctan( f_i/f_0)}{2 \pi f_i}$$

$$\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm}.$$

High–pass of Order N

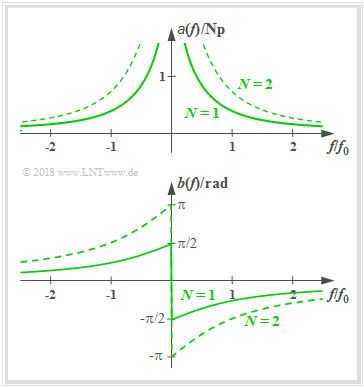
Attenuation function $a(f)$ and phase function $b(f)$ of a high–pass of order $N$

The frequency response of a realizable high–pass (HP) of order $N$ is:

$$H(f) = \left [\frac{ {\rm j}\cdot f/f_0 }{1 + {\rm j}\cdot f/f_0 }\right ]^N\hspace{0.05cm}.$$

For example the LC high pass is a first order high pass. Consequently we can obtain

• the attenuation function:

$$a(f) =N/2 \cdot \ln [1+( f_0/f)^2] \hspace{0.05cm},$$

• the phase function:

$$b(f) =-N \cdot \arctan( f_0/f) \hspace{0.05cm},$$

• the attenuation factor for the frequency $f=f_i$:

$$\alpha_i =|H(f = f_i)| = [1+( f_0/f_i)^2]^{-N/2}$$

$$\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)= \alpha_i \cdot A_i\cdot \cos(2\pi f_i t)\hspace{0.05cm},$$

• the phase delay for the frequency $f=f_i$:

$$\tau_i =\frac{b(f_i)}{2\pi f_i} = \frac{-N \cdot \arctan( f_0/f_i)}{2\pi f_i}$$

$$\Rightarrow \hspace{0.3cm} x(t)= A_i\cdot \cos(2\pi f_i t) \hspace{0.1cm}\rightarrow \hspace{0.1cm} y(t)=A_i\cdot \cos(2\pi f_i (t- \tau_i))\hspace{0.05cm}.$$

Phase function $b(f)$ of high–pass and low–pass

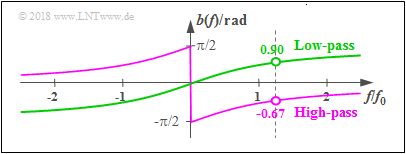
$\text{Example:}$  This graphic shows the phase function $b(f)$ with the cut–off frequency $f_0 = 1\ \rm kHz$ and order $N=1$

• of a low–pass (green curve),
• of a high–pass (violet curve).

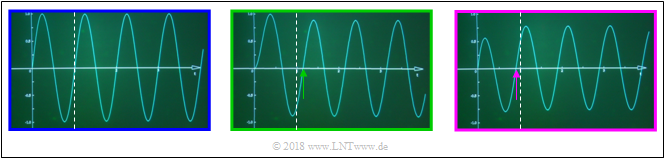
The input signal is sinusoidal with frequency $f_{\rm S} = 1.25\ {\rm kHz}$ whereby this signal is only turned on at $t=0$:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.75cm}0 \\ \sin(2\pi \cdot f_{\rm S} \cdot t ) \\ \end{array} \right.\quad\begin{array}{l} (t < 0), \\ (t>0). \\ \end{array}$$

The left graphic shows the signal $x(t)$. The dashed line marks the first zero at $t = T_0 = 0.8\ {\rm ms}$. The other two graphics show the output signals $y_{\rm LP}(t)$ und $y_{\rm HP}(t)$ of low–pass and high–pass, whereby the change in amplitude was balanced in both cases.

Input signal $x(t)$ (enframed in blue) as well as output signals $y_{\rm LP}(t)$ ⇒   green and $y_{\rm HP}(t)$ ⇒   magenta

• The first zero of the signal $y_{\rm LP}(t)$ after the low–pass is delayed by $\tau_{\rm LP} = 0.9/(2\pi) \cdot T_0 \approx 0.115 \ {\rm ms}$ compared to the first zero of $x(t)$   ⇒   marked with green arrow, whereby $b_{\rm LP}(f/f_{\rm S} = 0.9 \ {\rm rad})$ was considered.
• In contrast, the phase delay of the high–pass is negative: $\tau_{\rm HP} = -0.67/(2\pi) \cdot T_0 \approx -0.085 \ {\rm ms}$ and therefore the first zero of $y_{\rm HP}(t)$ occurs before the dashed line.
• Following this transient response, in both cases the zero crossings again come in the raster of the period duration $T_0 = 0.8 \ {\rm ms}.$

Remark: The shown signals were created using the interactive applet Causal systems – Laplace transform.

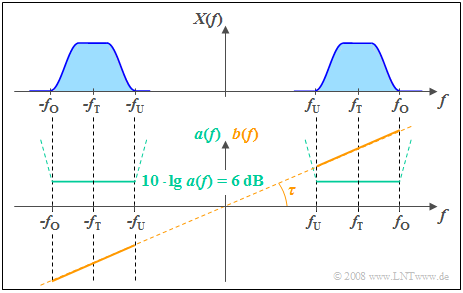
Attenuation and Phase Distortions

Requirements for a non–distorting channel

The adjacent figure shows

• the even attenuation function $a(f)$   ⇒   $a(-f) = a(f)$, and
• the uneven function curve $b(f)$   ⇒   $b(-f) = -b(- f)$

of a non–distorting channel. One can see:

• In a distortion–free system the attenuation function $a(f)$ must be constant between$f_{\rm U}$ and $f_{\rm O}$ around the carrier frequency $f_{\rm T}$, where the input signal exists   ⇒   $X(f) \ne 0$.
• From the specified constant attenuation value $6 \ \rm dB$ follows for the amplitude response $|H(f)| = 0.5$   ⇒   the signal values of all frequencies are thus halved by the system   ⇒   no attenuation distortions.
• In addition, in such a system, the phase function $b(f)$ between $f_{\rm U}$ and $f_{\rm O}$ must increase linearly with the frequency. As a result, all frequency components are delayed by the same phase delay $τ$   ⇒   no phase distortion.
• The delay $τ$ is fixed by the slope of $b(f)$. The phase function $b(f) \equiv 0$ would result in a delay–less system   ⇒   $τ = 0$.

The following summary considers that – in this applet – the input signal is always the sum of two harmonic oscillations,

$$x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right),$$

and therefore the channel influence is fully described by the attenuation factors $\alpha_1$ and $\alpha_2$ as well as the phase delays $\tau_1$ and $\tau_2$:

$$y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2).$$

$\text{Summary:}$ 

• A signal $y(t)$ is only distortion–free compared to $x(t)$ if $\alpha_1 = \alpha_2= \alpha$   and   $\tau_1 = \tau_2= \tau$   ⇒   $y(t) = \alpha \cdot x(t-\tau)$.
• Attenuation distortions occur when $\alpha_1 \ne \alpha_2$. If $\alpha_1 \ne \alpha_2$ and $\tau_1 = \tau_2$, then there are exclusively attenuation distortions.
• Phase distortions occur when $\tau_1 \ne \tau_2$. If $\tau_1 \ne \tau_2$ and $\alpha_1 = \alpha_2$, then there are exclusively phase distortions.

Exercises

• First choose an exercise number.
• An exercise description is displayed.
• Parameter values are adjusted to the respective exercises.
• Click „Hide solution” to display the solution.

Number „0” is a „Reset” button:

• Sets parameters to initial values (when loading the page).
• Displays a „Reset text” to describe the applet further.

(1)   We consider the parameters $A_1 = 0.8\ {\rm V}, \ A_2 = 0.6\ {\rm V}, \ f_1 = 0.5\ {\rm kHz}, \ f_2 = 1.5\ {\rm kHz}, \ \varphi_1 = 90^\circ, \ \varphi_2 = 30^\circ$ for the input signal $x(t)$.

Calculate the signal's period duration $T_0$ and power $P_x$. Can you read the value for $P_x$ off the applet?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}T_0 = \big [\hspace{-0.1cm}\text{ greatest common divisor }(0.5 \ {\rm kHz}, \ 1.5 \ {\rm kHz})\big ]^{-1}\hspace{0.15cm}\underline{ = 2.0 \ {\rm ms}};$

$\hspace{1.85cm} P_x = A_1^2/2 + A_2^2/2 \hspace{0.15cm}\underline{= 0.5 \ {\rm V^2}} = P_\varepsilon\text{, if }\hspace{0.15cm}\underline{k_{\rm M} = 0} \ \Rightarrow \ z(t) \equiv 0$.

(2)  Vary $\varphi_2$ between $\pm 180^\circ$ while keeping all other parameters from Exercise (1). How does the value of $T_0$ and $P_x$ change?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{No changes:}\hspace{0.2cm}\hspace{0.15cm}\underline{ T_0 = 2.0 \ {\rm ms}; \hspace{0.2cm} P_x = 0.5 \ {\rm V^2}}$.

(3)   Vary $f_2$ between $0 \le f_2 \le 10\ {\rm kHz}$ while keeping all other parameters from Exercise (1). How does the value of $P_x$ change?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{No changes if }f_2 \ne 0\text{ and } f_2 \ne f_1\text{:}\hspace{0.3cm} \hspace{0.15cm}\underline{P_x = 0.5 \ {\rm V^2}}\text{.} \hspace{0.2cm} T_0 \text{ changes if }f_2\text{is not a multiple of }f_1$.

$\hspace{1.85cm}\text{If }f_2 = 0\text{:}\hspace{0.2cm} P_x = A_1^2/2 + A_2^2\hspace{0.15cm}\underline{ = 0.68 \ {\rm V^2}}$. $\hspace{3cm}$

$\hspace{1.85cm}\text{If }f_2 = f_1\text{:}\hspace{0.2cm} P_x = [A_1\cos(\varphi_1) + A_2\cos(\varphi_2)]^2/2 + [A_1\sin(\varphi_1) + A_2\sin(\varphi_2)]^2/2 \text{.}$

$\hspace{1.85cm}\text{With } \varphi_1 = 90^\circ, \ \varphi_2 = 30^\circ\text{:}\hspace{0.3cm}\hspace{0.15cm}\underline{ P_x = 0.74 \ {\rm V^2}}\text{.}$

(4)   Keeping the previous input signal $x(t)$, set following parameters

$\alpha_1 = \alpha_2 = 0.5, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$, $k_{\rm M} = 1 \text{ and } \tau_{\rm M} = 0$ .

Are there linear distortions? Calculate the received power $P_y$ and the power $P_\varepsilon$ of the differential signal $\varepsilon(t) = z(t) - x(t)$.

$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{ y(t) = 0.5 \cdot x(t- 1\ {\rm ms})}\text{ is only attenuated and delayed, but not distorted.}$

$\hspace{1.85cm}\text{Received power:}\hspace{0.2cm} P_y = (A_1/2)^2/2 + (A_2/2)^2/2\hspace{0.15cm}\underline{ = 0.125 \ {\rm V^2}}\text{. } P_\varepsilon \text{ is significantly larger:} \hspace{0.1cm} \hspace{0.15cm}\underline{P_\varepsilon = 0.625 \ {\rm V^2}}.$

(5)   With the same settings as in Exercise (4), vary the matching parameters $k_{\rm M} \text{ and } \tau_{\rm M}$. How big is the distortion power $P_{\rm D}$?

$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D}\text{ is equal to }P_\varepsilon \text{ when using the ideal matching parameters:} \hspace{0.2cm}k_{\rm M} = 2 \text{ and } \tau_{\rm M}=T_0 - 0.5\ {\rm ms} = 1.5\ {\rm ms}$

$\hspace{1.0cm}\Rightarrow \hspace{0.3cm}z(t) = x(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\varepsilon(t) = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm D}\hspace{0.15cm}\underline{ = P_\varepsilon = 0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{Neither attenuation nor phase distortion.}$

(6)   The channel parameters are now set to: $\alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}$. Calculate the distortion power $P_{\rm D}$ and the Signal-to-Distortion ratio $(\rm SDR) \ \rho_{\rm D}$.

$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ when using the best matching parameters:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.24} \text{ and } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.5\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.059 \ {\rm V^2}}$.

$\hspace{1.85cm}\text{Attenuation distortions only.} \hspace{0.3cm}\text{Signal-to-Distortion-Ratio}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 8.5}$.

(7)   The channel parameters are now set to: $\alpha_1 = \alpha_2 = 0.5, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}$. Calculate the distortion power $P_{\rm D}$ and the the Signal-to-Distortion ratio $\rho_{\rm D}$.

$\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{when using the best matching parameters:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.84} \text{ and } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.071 \ {\rm V^2}}$.

$\hspace{1.85cm}\text{Phase distortions only.} \hspace{0.3cm}\text{Signal-to-Distortion-Ratio}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 7}$.

(8)   The channel parameters are now set to: $\hspace{0.15cm}\underline{\alpha_1 = 0.5} , \hspace{0.15cm}\underline{\alpha_2 = 0.2} , \ \hspace{0.15cm}\underline{\tau_1= 0.5\ {\rm ms} }, \ \hspace{0.15cm}\underline{\tau_2 = 0.3\ {\rm ms} }$. Are there attenuation distortions? Are there phase distortions? How can $y(t)$ be approximated? Hint: $\cos(3x) = 4 \cdot \cos^3(x) - 3\cdot \cos(x).$

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Both attenuation and phase distortions, because }\alpha_1 \ne \alpha_2\text{ and }\tau_1 \ne \tau_2$.

$\hspace{1.85cm}y(t) = y_1(t) + y_2(t)\ \Rightarrow \ y_1(t) = A_1 \cdot \alpha_1 \cdot \sin[2\pi f_1\ (t- 0.5\ \rm ms)] = -0.4 \ {\rm V} \cdot \cos(2\pi f_1 t)$

$\hspace{1.85cm} y_2(t) = \alpha_2 \cdot x_2(t- \tau_2) \text{ mit }x_2(t) = A_2 \cdot \cos[2\pi f_2\ (t- 30^\circ)] \approx A_2 \cdot \cos[2\pi f_2\ (t- 1/36 \ \rm ms)]$

$\hspace{1.85cm} \Rightarrow \ y_2(t) = 0.12 \ {\rm V} \cdot \cos[2\pi f_2\ (t- 0.328 \ {\rm ms})] \approx -0.12 \ { \rm V} \cdot \cos[2\pi f_2t]$.

$\hspace{1.85cm} \Rightarrow \ y(t) = y_1(t) + y_2(t) \approx -0.4 \ {\rm V} \cdot [\cos(2\pi \cdot f_1\cdot t) + 1/3 \cdot \cos(2\pi \cdot 3 f_1 \cdot t) = -0.533 \ {\rm V} \cdot \cos^3(2\pi f_1 t)$.

(9)   Using the parameters from Exercise (8), calculate the distortion power $P_{\rm D}$ and the the Signal-to-Distortion ratio $\rho_{\rm D}$.

$\hspace{1.0cm}\text{Best possible adaptation:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.96} \text{, } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.65\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.15 \ {\rm V^2} },\hspace{0.1cm}\hspace{0.15cm}\underline{\rho_{\rm D} = 0.500/0.15 \approx 3.3}$.

(10)  Now we set $A_2 = 0$ and $A_1 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ$. The channel is a Low-pass of order 1 $\underline{(f_0 = 1\ {\rm kHz})}$.
Are there any attenuation and/or phase distortions? Calculate the channel coefficients $\alpha_1$ and $\tau_1$.

$\hspace{1.0cm}\text{At only one frequency there are neither attenuation nor phase distortions.}$ $\hspace{1.0cm}\text{Attenuation factor for }f_1=f_0\text{ and }N=1\text{: }\alpha_1 =|H(f = f_1)| = [1+( f_1/f_0)^2]^{-N/2} = 2^{-1/2}= 1/\sqrt{2}\hspace{0.15cm}\underline{=0.707},$ $\hspace{1.0cm}\text{Phase factor for }f_1=f_0\text{ and }N=1\text{: }\tau_1 = N \cdot \arctan( f_1/f_0)/(2 \pi f_1)=\arctan( 1)/(2 \pi f_1) =1/(8f_1) \hspace{0.15cm}\underline{=0.125 \ \rm ms}.$

(11)   How do the channel parameters change when using a Low-pass of order 2 compared to a Low-pass of order 1 $(f_0 = 1\ {\rm kHz})$?

$\hspace{1.0cm}\alpha_1 = 0.707^2 = 0.5$ and $\tau_1 = 2 \cdot 0.125 = 0.25 \ {\rm ms}$.

$\hspace{1.0cm}\text{The signal }y(t)\text{ is only half as big as }x(t)\text{ and is retarded: The cosine turns into a sine function}$.

(12)   What differences arise when using a High-pass of order 2 compared to a Low-pass of order 2 $(f_0 = 1\ {\rm kHz})$?

$\hspace{1.0cm}\text{Since }f_1 = f_0\text{ the attenuation factor }\alpha_1 = 0.5\text{ stays the same and }\tau_1 = -0.25 \ {\rm ms}\text{ which means:}$

$\hspace{1.0cm}\text{The signal }y(t)\text{ is also only half as big as }x(t)\text{ and precedes it: The cosine turns into the Minus–sine function}$.

(13)   What differences at the signal $y(t)$ can be observed between the Low-pass and the High-pass of order 2 $(f_0 = 1\ {\rm kHz})$ when you start with the initial input signal according to Exercise (1) and continuously raise $f_2$ up to $10 \ \rm kHz$ ?

$\hspace{1.0cm}\text{With the Low-pass the second term is increasingly suppressed. For }f_2 = 10 \ {\rm kHz}\text{: }y_{\rm LP}(t) \approx 0.8 \cdot x_1(t-0.3 \ \rm ms).$

$\hspace{1.0cm}\text{With the High-pass however the second term dominates. For }f_2 = 10 \ {\rm kHz}\text{: }y_{\rm HP}(t) \approx 0.2 \cdot x_1(t+0.7 \ {\rm ms}) + x_2(t).$

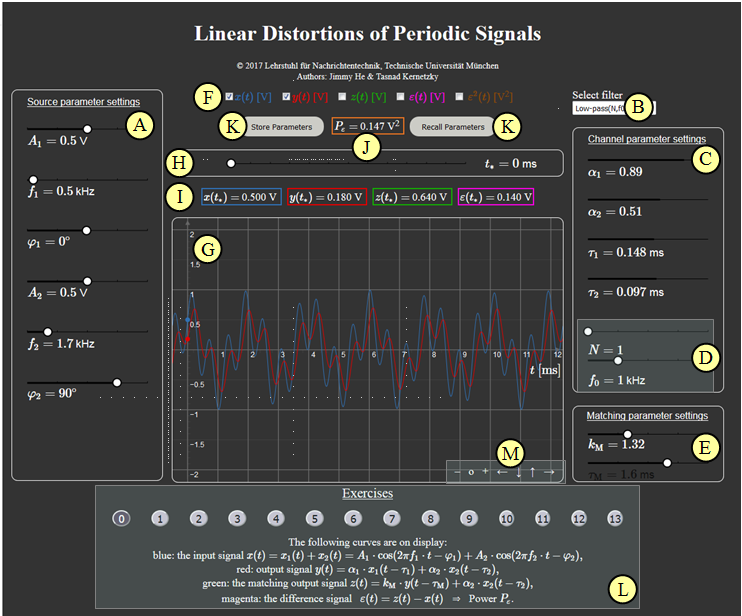
Applet Manual

    (A)     Parameter selection for input signal $x(t)$ per slider: Amplitude, frequency, phase values

    (B)     Preselection for channel parameters per slider: Low-pass or High-pass

    (C)     Selction of channel parameters per slider: Dämpfungsfaktoren und Phasenlaufzeiten

    (D)     Selection of channel parameters for High and Low pass: Order$n$, cut-off-frequency $f_0$

    (E)     Selection of matching parameters $k_{\rm M}$ and $\varphi_{\rm M}$

    (F)     Selection of the signals to be displayed: $x(t)$, $y(t)$, $z(t)$, $\varepsilon(t)$, $\varepsilon^2(t)$

    (G)     Graphic display of the signals

    (H)     Enter the time $t_*$ for the numeric output

    ( I )     numeric output of the signal values $x(t_*)$, $y(t_*)$, $z(t_*)$ and $\varepsilon(t_*)$

    (J)     Numeric output of the main result $P_\varepsilon$

    (K)     Save and reall parameters

    (L)     Exercises: Exercise selection, description and solution

    (M)     Variation possibilities for the graphic display

$\hspace{1.5cm}$Zoom–functions „$+$” (scale up), „$-$” (scale down) und $\rm o$ (reset)

$\hspace{1.5cm}$Move with „$\leftarrow$” (section to the left, ordinate to the right), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”

$\hspace{1.5cm}$'Other options:

$\hspace{1.5cm}$Hold shift and scroll: Zoom in on/out of coordinate system,

$\hspace{1.5cm}$Hold shift and left click: Move the coordinate system.

About the Authors

This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technische Universität München.

• The original version was created in 2005 by Bettina Hirner as part of her Diploma thesis using „FlashMX–Actionscript” (Supervisor: Günter Söder ).
• In 2018 this Applet was redesigned and updated to „HTML5” by Jimmy He as part of his Bachelor's thesis (Supervisor: Tasnád Kernetzky) .

Once again: Open Applet in new Tab

Open Applet in new Tab