Exercise 2.5Z: Multi-Path Scenario

• Zurück zum Buch

Mobilfunk–Szenario mit drei Pfaden

In  Exercise 2.5, a delay–Doppler function (or scatter function) was given. From this, we will calculate and interpret the other system functions. The given scatter function  $s(\tau_0, f_{\rm D})$  was

$$s(\tau_0, f_{\rm D}) =\frac{1}{\sqrt{2}} \cdot \delta (\tau_0) \cdot \delta (f_{\rm D} - 100\,{\rm Hz}) \ - \ $$

$$\hspace{1.5cm} \ - \ \hspace{-0.2cm} \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm \mu s}) \cdot \delta (f_{\rm D} \hspace{-0.05cm}- \hspace{-0.05cm}50\,{\rm Hz}) \ - \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm \mu s}) \cdot \delta (f_{\rm D}\hspace{-0.05cm} + \hspace{-0.05cm}50\,{\rm Hz}) \hspace{0.05cm}.$$

Note:   In our learning tutorial,  $s(\tau_0, \hspace{0.05cm} f_{\rm D})$  is also identified with  $\eta_{\rm VD}(\tau_0, \hspace{0.05cm}f_{\rm D})$ .

Here we have replaced the delay variable  $\tau$  with  $\tau_0$ . The new variable  $\tau_0$  describes the difference between the delay of a path and the delay  $\tau_1$  of the main path. The main path is thus identified in the above equation by  $\tau_0 = 0$ .

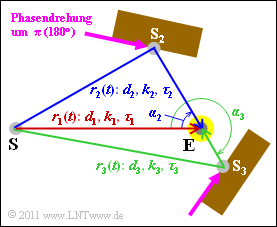
Now, we try to find a mobile radio scenario in which this scatter function would actually occur. The basic structure is sketched above as a top view, and the following hold:

• A single frequency is transmitted  $f_{\rm S} = 2 \ \rm GHz$.
• The mobile receiver  $\rm (E)$  is represented here by a yellow dot. It is not known whether the vehicle is stationary, moving towards the transmitter  $\rm (S)$  or moving away from it.
• The signal reaches the receiver via a main path (red) and two secondary paths (blue and green). Reflections from the obstacles cause phase shifts of  $\pi$.
• ${\rm S}_2$  and  ${\rm S}_3$  are to be understood here as fictitious transmitters from whose position the angles of incidence  $\alpha_2$  and  $\alpha_3$  of the secondary paths can be determined.
• Let the signal frequency be   $f_{\rm S}$, the angle of incidence   $\alpha$, the velocity  $v$  and the velocity of light  $c = 3 \cdot 10^8 \ \rm m/s$. Then, the Doppler frequency is

$$f_{\rm D}= {v}/{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm}.$$

• The damping factors  $k_1$,  $k_2$  and  $k_3$  are inversely proportional to the path lengths  $d_1$,  $d_2$  and  $d_3$. This corresponds to the path loss exponent  $\gamma = 2$.
• This means:   The signal power decreases quadratically with distance  $d$  and accordingly the signal amplitude decreases linearly with  $d$.

Notes:

• This task belongs to chapter  Das GWSSUS–Kanalmodell.
• We focus especially on the   path-loss model  and the   Doppler effect.

Questionnaire

1

At first, consider only the Dirac function at  $\tau = 0$  and  $f_{\rm D} = 100 \ \rm Hz$. Which statements apply to the receiver?

	The receiver is standing.
	The receiver moves directly towards the transmitter.
	The receiver moves away in the opposite direction to the transmitter.

2

What is the vehicle speed?

$v \ = \ $ $\ \ \rm km/h$

3

Which statements apply to the Dirac at  $\tau_0 = 1 \ \ \rm µ s$  and  $f_{\rm D} = +50 \ \ \rm Hz$?

	This Dirac comes from the blue path.
	This Dirac comes from the green path.
	The angle  is  $30^\circ$.
	The angle  is  $60^\circ$.

4

What statements apply to the green path?

	We have $\tau_0 = 1 \ \ \rm µ s$  and  $f_{\rm D} = \, –50 \ \ \rm Hz$.
	The angle  $\alpha_3$  (see graph) is  $60^\circ$.
	The angle  $\alpha_3$  is  $240^\circ$.

5

Which of the following relations hold between the two side paths?

	$d_3 = d_2$.
	$k_3 = k_2$.
	$\tau_3 = \tau_2$.

6

What is the difference in time  $\Delta d = d_2 - d_1$?

$\Delta d \ = \ $ $\ \ \rm m$

7

What is the relationship between  $d_2$  and  $d_1$?

$d_2/d_1 \ = \ $

8

Find the distances  $d_1$  and  $d_2$ .

$d_1 \ = \ $ $\ \rm m$

$d_2 \ = \ $ $\ \rm m$

Sample solution

Musterlösung

(1)  The Doppler frequency is positive for $\tau_0$. This means that the receiver is moving towards the transmitter   ⇒   solution 2 is correct.

(2)  The equation for the Doppler frequency is

$$f_{\rm D}= \frac{v}{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm},$$

If the angle of incidence is $\alpha=0$, the Doppler frequency is

$$f_d=\frac{v}{c}\cdot f_S$$

• The speed of the receiver is then

$$v = \frac{f_{\rm D}}{f_{\rm S}} \cdot c = \frac{10^2\,{\rm Hz}}{2 \cdot 10^9\,{\rm Hz}} \cdot 3 \cdot 10^8\,{\rm m/s} = 15\,{\rm m/s} \hspace{0.1cm} \underline {= 54 \,{\rm km/h}} \hspace{0.05cm}.$$

(3)  Solutions 1 and 4 are correct:

• The Doppler frequency $f_{\rm D} = 50 \ \rm Hz$ comes from the blue path, because the receiver moves towards the virtual transmitter ${\rm S}_2$ (i.e., towards the reflection point), although not directly. In other words, the movement of the receiver reduces the blue path's length.
• The angle $\alpha_2$ between the direction of movement and the connecting line ${\rm S_2 – E}$ is $60^\circ$:

$$\cos(\alpha_2) = \frac{f_{\rm D}}{f_{\rm S}} \cdot \frac{c}{v} = \frac{50 \,{\rm Hz}\cdot 3 \cdot 10^8\,{\rm m/s}}{2 \cdot 10^9\,{\rm Hz}\cdot 15\,{\rm m/s}} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha_2 \hspace{0.1cm} \underline {= 60^{\circ} } \hspace{0.05cm}.$$

(4)  Statements 1 and 3 are correct:

• From $f_{\rm D} = \, –50 \ \rm Hz$ follows $\alpha_3 = \alpha_2 ± \pi$, so $\alpha_3 \ \underline {= 240^\circ}$.

(5)  All statements are correct:

• The two Dirac functions at $± 50 \ \ \rm Hz$ have the same delay. We have $\tau_3 = \tau_2 = \tau_1 + \tau_0$.
• From the equality of the delays, however, also follows that  $d_3 = d_2$. As both paths have the same length, their damping factors are also equal.

(6)  The delay difference is $\tau_0 = 1 \ \rm µ s$, as shown in the equation for $s(\tau_0, f_{\rm D})$.

• This gives the difference in length:

$$\Delta d = \tau_0 \cdot c = 10^{–6} {\rm s} \cdot 3 \cdot 10^8 \ \rm m/s \ \ \underline {= 300 \ \ \rm m}.$$

(7)  The path loss exponent was assumed to be $\gamma = 2$ for this task.

• Then $k_1 = K/d_1$ and $k_2 = K/d_2$.

• The minus sign takes into account the $180^\circ$ phase rotation on the secondary paths.
• From the weights of the Dirac functions one can read $k_1 = \sqrt{0.5}$ and $k_2 = -0.5$. From this follows:

$$\frac{d_2}{d_1} = \frac{k_1}{-k_2} = \frac{1/\sqrt{2}}{0.5} = \sqrt{2} \hspace{0.15cm} \underline {= 1.414} \hspace{0.05cm}.$$

• The constant $K$ is only an auxiliary variable that does not need to be considered further.

(8)  From   $d_2/d_1 = 2^{-0.5}$  and  $\Delta d = d_2 \, - d_1 = 300 \ \rm m$  finally follows:

$$\sqrt{2} \cdot d_1 - d_1 = 300\,{\rm m} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_1 = \frac{300\,{\rm m}}{\sqrt{2} - 1} \hspace{0.15cm} \underline {= 724\,{\rm m}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_2 = \sqrt{2} \cdot d_1 \hspace{0.15cm} \underline {= 1024\,{\rm m}} \hspace{0.05cm}.$$