Exercise 2.2Z: Real Two-Path Channel

• Zurück zum Buch

Zweiwege–Szenario

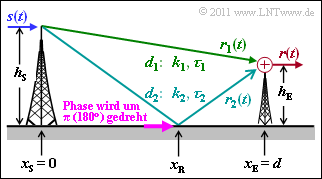
Betrachtet wird das skizzierte Szenario, bei dem das Sendesignal  $s(t)$  die Antenne des Empfängers über zwei Wege erreicht:

$$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) \hspace{0.05cm}.$$

Dabei ist zu beachten:

• Die Laufzeiten  $\tau_1$  und  $\tau_2$  auf Haupt– und Nebenpfad können aus den Pfadlängen  $d_1$  und  $d_2$  unter Verwendung der Lichtgeschwindigkeit  $c = 3 \cdot 10^8 \ \rm m/s$  berechnet werden.
• Die Amplitudenfaktoren  $k_1$  und  $k_2$  sollen vereinfachend gemäß dem Pfadverlustmodell mit dem Pfadverlustexponenten  $\gamma = 2$  angenommen werden (Freiraumdämpfung).
• Die Höhe der Sendeantenne ist  $h_{\rm S} = 500 \ \rm m$, die der Empfangsantenne  $h_{\rm E} = 30 \ \rm m$. Die Antennen stehen im Abstand von  $d = 10 \ \rm km$.
• Die Reflektion auf dem Nebenpfad führt zu einer Phasenänderung um  $\pi$, so dass man die Teilsignale subtrahieren muss. Dies wird durch einen negativen  $k_2$–Wert berücksichtigt.

Hinweis:

• Die Aufgabe gehört zum Kapitel  Mehrwegeempfang beim Mobilfunk.

Fragebogen

1

Berechnen Sie die Länge  $d_1$  des direkten Pfades.

$d_1 \ = \ $ $\ \rm m$

2

Berechnen Sie die Länge  $d_2$  des Umwegpfades.

$d_2 \ = \ $ $\ \rm m$

3

Welche Differenzen  $\Delta d = d_2 \ - d_1$  und  $\Delta \tau = \tau_2 -\tau_1$  (Laufzeit) ergeben sich nach exakter Rechnung?

$\Delta d \ = \ $ $\ \rm m$

$\Delta \tau \ = \ $ $\ \rm ns$

4

Welche Gleichung ergibt sich für die Laufzeitdifferenz  $\Delta \tau$  mit der für kleine  $\varepsilon$  gültigen Näherung $\sqrt{(1 + \varepsilon)} \approx 1 + \varepsilon/2$?

	$\Delta \tau = (h_{\rm S} \ - h_{\rm E})/d$,
	$\Delta \tau = (h_{\rm S} \ - h_{\rm E})/(c \cdot d)$,
	$\Delta \tau = 2 \cdot h_{\rm S} \cdot h_{\rm E}/(c \cdot d)$.

5

Welche Aussagen treffen für die Amplitudenkoeffizienten  $k_1$  und  $k_2$  zu?

	Die Koeffizienten  $k_1$  und  $k_2$  sind betragsmäßig nahezu gleich.
	Die Beträge  $|k_1|$  und  $|k_2|$  unterscheiden sich deutlich.
	Die Koeffizienten  $|k_1|$  und  $|k_2|$  unterscheiden sich im Vorzeichen.

Musterlösung

Musterlösung

(1)  Mit den Bezeichnungen in der Veranschaulichungsskizze ergibt sich nach „Pythagoras”:

$$d_1 = \sqrt{d^2 + (h_{\rm S}- h_{\rm E})^2} = \sqrt{10^2 + (0.5- 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10011.039\,{\rm m}} \hspace{0.05cm}.$$

• Eigentlich ist die Angabe einer solchen Länge mit der Genauigkeit eines Millimeters nicht sehr sinnvoll und widerspricht der Mentalität eines Ingenieurs.
• Wir haben das hier trotzdem gemacht, um die Genauigkeit der in der Teilaufgabe (4) gesuchten Näherung überprüfen zu können.

(2)  Klappt man den reflektierten Strahl rechts vpn $x_{\rm R}$ nach unten (Spiegelung am Erdboden), so erhält man wiederum ein rechtwinkliges Dreieck. Daraus folgt:

$$d_2 = \sqrt{d^2 + (h_{\rm S}+ h_{\rm E})^2} = \sqrt{10^2 + (0.5+ 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10014.035\,{\rm m}} \hspace{0.05cm}.$$

(3)  Mit den Ergebnissen aus (1) und (2) erhält man für die Längen– und die Laufzeitdifferenz:

$$\Delta d = d_2 - d_1 = \hspace{0.1cm} \underline {=2.996\,{\rm m}} \hspace{0.05cm},\hspace{1cm} \Delta \tau = \frac{\Delta d}{c} = \frac{2.996\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s}} \hspace{0.1cm} \underline {=9.987\,{\rm ns}} \hspace{0.05cm}.$$

(4)  Mit $h_{\rm S} + h_{\rm E} \ll d$ lassen sich die obigen Gleichung wie folgt ausdrücken:

$$d_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}- h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}- h_{\rm E})^2}{2d^2} \right ] \hspace{0.05cm},\hspace{1cm} d_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{2d^2} \right ]$$

$$\Rightarrow \hspace{0.3cm} \Delta d = d_2 - d_1 \approx \frac {1}{2d} \cdot \left [ (h_{\rm S}+ h_{\rm E})^2 - (h_{\rm S}- h_{\rm E})^2 \right ] = \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{d}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \Delta \tau = \frac{\Delta d}{c} \approx \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{c \cdot d} \hspace{0.05cm}.$$

• Richtig ist also der Lösungsvorschlag 3. Mit den vorgegebenen Zahlenwerten erhält man hierfür:

$$\Delta \tau \approx \frac {2 \cdot 500\,{\rm m}\cdot 30\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s} \cdot 10000\,{\rm m}} = 10^{-8}\,{\rm s} = 10\,{\rm ns} \hspace{0.05cm}.$$

• Die relative Verfälschung gegenüber dem tatsächlichen Wert entsprechend Teilaufgabe (3) beträgt nur $0.13\%$.
• Beim Lösungsvorschlag 1 stimmt schon die Einheit nicht.
• Bei Lösungsvorschlag 2 käme es zu keiner Laufzeitverschiebung, wenn beide Antennen die gleiche Höhe hätten. Dies trifft sicher nicht zu.

(5)  Der Pfadverlustexponent $\gamma = 2$ sagt aus, dass die Empfangsleistung $P_{\rm E}$ quadratisch mit der Distanz abnimmt.

• Die Signalamplitude nimmt also mit $1/d$ ab, und mit einer Konstanten $K$ gilt:

$$k_1 = \frac {K}{d_1} \hspace{0.05cm},\hspace{0.2cm}|k_2| = \frac {K}{d_2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {|k_2|}{k_1} = \frac {d_1}{d_2}= \frac {10011.039\,{\rm m}}{10014.035\,{\rm m}} \approx 0.99 \hspace{0.05cm}.$$

• Die beiden Pfadgewichte unterscheiden sich somit im Betrag nur um etwa $1\%$.
• Allerdings haben die Koeffizienten $k_1$ und $k_2$ verschiedene Vorzeichen   ⇒   Richtig sind die Antworten 1 und 3.