Exercise 1.2: Lognormal Channel Model

• Zurück zum Buch

WDF des Lognormal–Fadings

Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand  $d_0$  von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation.

Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar:

$$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$

• $V_0$  berücksichtigt den entfernungsabhängigen Pfadverlust, der mit  $V_0 = 80 \ \rm dB$  als konstant angenommen wird.
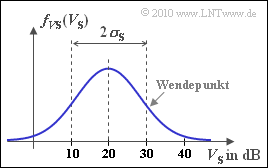
• Der Verlust  $V_{\rm S}$  ist auf Abschattungen (Shadowing) zurückzuführen, der durch die Lognormal–Verteilung mit der Wahrscheinlichkeitsdichtefunktion

$$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$

ausreichend genau beschrieben wird (siehe Grafik). Es gelten folgende Zahlenwerte:

$$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (Teilaufgabe\hspace{0.15cm} 2)}\hspace{0.05cm}.$$

Gehen Sie außerdem von folgenden einfachen Annahmen aus:

• Die Sendeleistung beträgt  $P_{\rm S} = 10 \ \rm W$  (oder $40 \ \rm dBm$).
• Die Empfangsleistung soll mindestens  $P_{\rm E} = 10 \ \rm pW$  (umgerechnet: $–80 \ \rm dBm$) betragen.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Distanzabhängige Dämpfung und Abschattung.

• Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden:

$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$

• Oder Sie benutzen das von $\rm LNTwww$ bereitgestellte Interaktionsmodul Komplementäre Gaußsche Fehlerfunktionen.

Fragebogen

1

Wäre  $P_{\rm E}$  ohne Berücksichtigung des Lognormal–Fadings ausreichend?

	Ja,
	Nein.

2

Die Lognormal–Parameter seien  $m_{\rm S} = 20 \, \rm dB$  und  $\sigma_{\rm S} = 0 \, \rm dB$. In wieviel Prozent der Zeit funktioniert das System?

${\rm Pr(System \ funktioniert)} \ = \ $ $\ \%$

3

Welche Wahrscheinlichkeit ergibt sich mit  $m_{\rm S} = 20 \ \rm dB$  und  $\sigma_{\rm S} = 10 \ \rm dB$?

${\rm Pr(System \ funktioniert)}\ = \ $ $\ \%$

4

Wie groß darf  $V_0$  maximal sein, damit die Zuverlässigkeit zu  $99.9\%$  erreicht wird?

$V_0 \ = \ $ $\ \rm dB$

Musterlösung

Musterlösung

(1)  Richtig ist JA:

• Aus dem $\rm dB$–Wert $V_0 = 80 \ \rm dB$ folgt der absolute (lineare) Wert $K_0 = 10^8$. Damit beträgt die Empfangsleistung

$$P_{\rm E} = P_{\rm S}/K_0 = 10 \ {\rm W}/10^8 = 100 \ {\rm nW} > 10 \ \rm pW.$$

• Man kann dieses Problem auch direkt mit den logarithmischen Größen lösen:

$$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}{1\,\,{\rm mW}} = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm S}}{1\,\,{\rm mW}} - V_0 = 40\,{\rm dBm} -80\,\,{\rm dB} = -40\,\,{\rm dBm} \hspace{0.05cm}.$$

• Gefordert ist aber lediglich der Grenzwert $–80 \ \rm dBm$.

(2)  Lognormal–Fading mit $\sigma_{\rm S} = 0 \ \rm dB$ ist gleichbedeutend mit einer konstanten Empfangslestung $P_{\rm E}$.

• Gegenüber der Teilaufgabe (1) ist diese um $m_{\rm S} = 20 \ \rm dB$ kleiner   ⇒   $P_{\rm E} = \ –60 \ \rm dBm$.
• Sie ist aber immer noch größer als der vorgegebene Grenzwert ($–80 \ \rm dBm$).
• Daraus folgt:   Das System ist (fast) zu 100% funktionsfähig. „Fast” deshalb, weil es bei einer Gaußschen Zufallsgröße immer eine (kleine) Restunsicherheit gibt.

(3)  Die Empfangsleistung ist dann zu gering (kleiner als $–80 \ \rm dBm$), wenn der Leistungsverlust durch den Lognormal–Term $40 \ \rm dB$ oder mehr beträgt.

• Der veränderliche Anteil $V_{\rm S}$ darf also nicht größer sein als $20 \ \rm dB$.
• Daraus folgt:

$${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{20\,\,{\rm dB}}{\sigma_{\rm S} = 10\,{\rm dB}}\right ) = {\rm Q}(2) \approx 0.02\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}({\rm "System\hspace{0.15cm}funktioniert"})= 1- 0.02 \hspace{0.15cm} \underline{\approx 98\,\%}\hspace{0.05cm}.$$

Verlust durch Lognormal–Fading

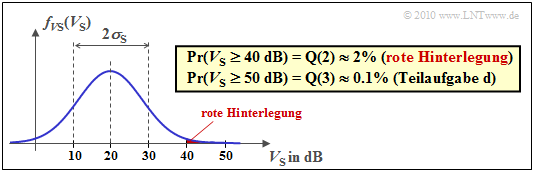
Die Grafik verdeutlicht das Ergebnis.

• Dargestellt ist hier die Wahrscheinlichkeitsdichte $f_{\rm VS}(V_{\rm S})$ des Pfadverlustes durch Shadowing (Longnormal–Fading).
• Die Wahrscheinlichkeit, dass das System ausfällt, ist rot markiert:

(4)  Aus der Verfügbarkeitswahrscheinlichkeit $99.9 \%$ folgt die Ausfallwahrscheinlichkeit $10^{\rm –3} \approx \ {\rm Q}(3)$.

• Verringert man den entfernungsabhängigen Pfadverlust $V_0$ um $10 \ \rm dB$ auf $\underline {70 \ \rm dB}$, so kommt es erst dann zu einem Ausfall, wenn $V_{\rm S} ≥ 50 \ \rm dB$ ist.
• Damit wäre genau die geforderte Zuverlässigkeit erreicht, wie die folgende Rechnung zeigt:

$${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{120-70-20}{10}\right ) = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.$$