Korrelation und Regressionsgerade

Applet in neuem Tab öffnen

Theoretischer Hintergrund

Erwartungswerte von 2D–Zufallsgrößen und Korrelationskoeffizient

Wir betrachten eine zweidimensionale  $\rm (2D)$–Zufallsgröße  $(X,\ Y)$  mit der Wahrscheinlichkeitsdichtefunktion  $\rm (WDF)$  $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten  $X$  und  $Y$  statistische Abhängigkeiten bestehen.  Ein Sonderfall ist die Korrelation.

$\text{Definition:}$  Unter  Korrelation  versteht man eine lineare Abhängigkeit  zwischen den Einzelkomponenten  $X$  und  $Y$.

• Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
• Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.

Für das Folgende setzen wir voraus, dass  $X$  und  $Y$  mittelwertfrei seien   ⇒   ${\rm E}\big [ X \big ] = {\rm E}\big [ Y \big ]=0$.  Zur Beschreibung der Korrelation genügen dann folgende Erwartungswerte:

• die  Varianzen  in  $X$–  bzw. in  $Y$–Richtung:

$$\sigma_X^2= {\rm E}\big [ X^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}x^2 \cdot f_{X}(x) \, {\rm d}x\hspace{0.05cm},\hspace{0.5cm}\sigma_Y^2= {\rm E}\big [Y^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}y^2 \cdot f_{Y}(y) \, {\rm d}y\hspace{0.05cm};$$

• die  Kovarianz  zwischen den Einzelkomponenten  $X$  und  $Y$:

$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\ \cdot y \cdot f_{XY}(x,y) \, {\rm d}x\, {\rm d}y\hspace{0.05cm}.$$

Bei statististischer Unabhängigkeit der beiden Komponenten  $X$  und  $Y$  ist die Kovarianz  $\mu_{XY} \equiv 0$. 

• Das Ergebnis  $\mu_{XY} = 0$  ist auch bei statistisch abhängigen Komponenten  $X$  und  $Y$  möglich, nämlich dann, wenn diese unkorreliert, also  linear unabhängig  sind.
• Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung  $Y=X^2.$

Man spricht dann von  vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen  $X$  und  $Y$  durch die Gleichung  $Y = K · X$  ausgedrückt wird.

Dann ergibt sich für die Kovarianz:

• $\mu_{XY} = σ_X · σ_Y$  bei positivem Wert von  $K$,
• $\mu_{XY} = -σ_X · σ_Y$  bei negativem  $K$–Wert.

Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.

$\text{Definition:}$  Der  Korrelationskoeffizient  ist der Quotient aus der Kovarianz  $\mu_{XY}$  und dem Produkt der Effektivwerte  $σ_X$  und  $σ_Y$  der beiden Komponenten:

$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}.$$

Der Korrelationskoeffizient  $\rho_{XY}$  weist folgende Eigenschaften auf:

• Aufgrund der Normierung gilt stets  $-1 \le ρ_{XY} ≤ +1$.
• Sind die beiden Zufallsgrößen  $X$  und  $Y$  unkorreliert, so ist  $ρ_{XY} = 0$.
• Bei strenger linearer Abhängigkeit zwischen  $X$  und  $Y$  ist  $ρ_{XY}= ±1$   ⇒   vollständige Korrelation.
• Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem  $X$–Wert im statistischen Mittel auch  $Y$  größer ist als bei kleinerem  $X$.
• Dagegen drückt ein negativer Korrelationskoeffizient aus, dass  $Y$  mit steigendem  $X$  im Mittel kleiner wird.

2D-WDF  $f_{XY}(x, y)$  sowie die zugehörigen Randwahrscheinlichkeitsdichten  $f_{X}(x)$  und  $f_{Y}(y)$

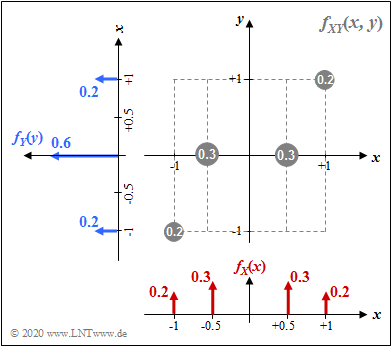
$\text{Beispiel 1:}$  Die 2D–Zufallsgröße  $(X,\ Y)$  sei diskret und kann nur vier verschiedene Werte annehmen:

• $(+0.5,\ 0)$  sowie $(-0.5,\ 0)$  jeweils mit der Wahrscheinlichkeit  $0.3$,
• $(+1,\ +\hspace{-0.09cm}1)$  sowie $(-1,\ -\hspace{-0.09cm}1)$  jeweils mit der Wahrscheinlichkeit  $0.2$.

$\rm (A)$  Die Varianzen bzw. die Streuungen können aus   $f_{X}(x)$  und  $f_{Y}(y)$  berechnet werden:

$$\sigma_X^2 = 2 \cdot \big [0.2 \cdot 1^2 + 0.3 \cdot 0.5^2 \big] = 0.55\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_X = 0.7416,$$

$$\sigma_Y^2 = \big [0.2 \cdot (-1)^2 + 0.6 \cdot 0^2 +0.2 \cdot (+1)^2 \big] = 0.4\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_Y = 0.6325.$$

$\rm (B)$  Für die Kovarianz ergibt sich der folgende Erwartungswert:

$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = 2 \cdot \big [0.2 \cdot 1 \cdot 1 + 0.3 \cdot 0.5 \cdot 0 \big] = 0.4.$$

$\rm (C)$  Damit erhält man für den Korrelationskoeffizient:

$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}=\frac{0.4 } {0.7416 \cdot 0.6325 }\approx 0.8528.$$

Regressionsgerade

Gaußsche 2D-WDF mit Korrelationsgerade

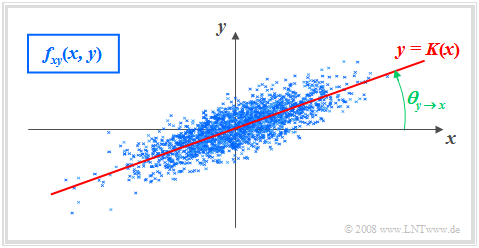
Ziel der linearen Regression ist es, einen einfachen (linearen) Zusammenhang zwischen zwei Zufallsgrößen  $X$  und  $Y$  zu anzugeben, deren $\text{2D-WDF}$  $f_{XY}(x, y)$  durch Punkte in der  $(x,\ y)$–Ebene vorgegeben ist. Die Skizze zeigt das Prinzip am Beispiel mittelwertfreier Größen:  Gesucht ist die Gleichung der Geraden  $R$  ⇒   $y=k_{\rm opt} \cdot x$  mit der Eigenschaft, dass der mittlere quadratische (Euklidische) Abstand  $\rm (MQA)$  aller Punkte von dieser Geraden minimal ist.

Bei einer großen Datenmenge ist der mathematische Aufwand beträchtlich, den bestmöglichen Parameter  $k_{\rm opt}$  zu ermitteln. Der Aufwand wird deutlich reduziert, wenn man den Abstand nur in  $x$– oder in $y$–Richtung definiert.

$$\text{Regressionsgerade }R_{y \to x}$$

Wir betrachten eine zweidimensionale  $\rm (2D)$–Zufallsgröße  $(X,\ Y)$  mit der Wahrscheinlichkeitsdichtefunktion  $\rm (WDF)$  $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten  $X$  und  $Y$  statistische Abhängigkeiten bestehen.  Ein Sonderfall ist die Korrelation.

Gaußsche 2D-WDF mit Korrelationsgerade

$\text{Definition:}$  Als  Korrelationsgerade  bezeichnet man die Gerade  $y = K(x)$  in der  $(x, y)$–Ebene durch den „Mittelpunkt”  $(m_x, m_y)$. Manchmal wird diese Gerade auch  Regressionsgerade  genannt.

Die Korrelationsgerade besitzt folgende Eigenschaften:

• Die mittlere quadratische Abweichung von dieser Geraden – in  $y$–Richtung betrachtet und über alle  $N$  Punkte gemittelt – ist minimal:

$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$

• Die Korrelationsgerade kann als eine Art  „statistische Symmetrieachse“  interpretiert werden. Die Geradengleichung lautet:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$

Der Winkel, den die Korrelationsgerade zur  $x$–Achse einnimmt, beträgt:

$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$

Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von  $y$  auf  $x$  handelt.

• Die Regression in Gegenrichtung – also von  $x$  auf  $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in  $x$–Richtung.

• Das interaktive Applet  Korrelationskoeffizient und Regressionsgerade  verdeutlicht, dass sich im Allgemeinen  $($falls  $σ_y \ne σ_x)$  für die Regression von  $x$  auf  $y$  ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:

$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$

Versuchsdurchführung

• Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
• Lösung nach Drücken von „Hide solution”.
• Aufgabenstellung und Lösung in Englisch.

Die Nummer 0 entspricht einem „Reset”:

• Gleiche Einstellung wie beim Programmstart.
• Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.

In der folgenden Beschreibung bedeutet

• Blau:   Verteilungsfunktion 1 (im Applet blau markiert),
• Rot:     Verteilungsfunktion 2 (im Applet rot markiert).

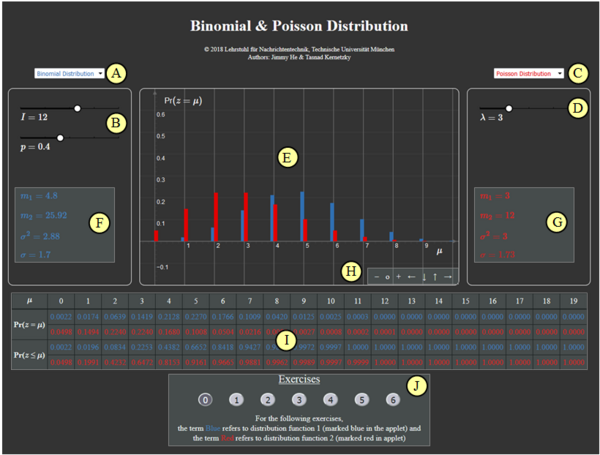
(1)  Setzen Sie Blau: Binomialverteilung $(I=5, \ p=0.4)$ und Rot: Binomialverteilung $(I=10, \ p=0.2)$.

Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$

(2)  Es gelten weiter die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder } {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$.

$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158.$

(3)  Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2;$

$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$

(4)  Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.

Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;

$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;

(5)  Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exakt)}$.

$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0 \ ( \approx 0)$

$\hspace{1.85cm} \text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16}/{16!}\approx 2 \cdot 10^{-22}$.

(6)  Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$

$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$

Zur Handhabung des Applets

    (A)     Vorauswahl für blauen Parametersatz

    (B)     Parametereingabe $I$ und $p$ per Slider

    (C)     Vorauswahl für roten Parametersatz

    (D)     Parametereingabe $\lambda$ per Slider

    (E)     Graphische Darstellung der Verteilungen

    (F)     Momentenausgabe für blauen Parametersatz

    (G)     Momentenausgabe für roten Parametersatz

    (H)     Variation der grafischen Darstellung

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

    ( I )     Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$

    (J)     Bereich für die Versuchsdurchführung

Andere Möglichkeiten zur Variation der grafischen Darstellung:

• Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
• Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen