Aufgabe 3.4: GMSK–Modulation

Verschiedene Signale der GMSK-Modulation

Das bei GSM eingesetzte Modulationsverfahren ist bekanntlich Gaussian Minimum Shift Keying, abgekürtzt $\rm GMSK$. Dabei handelt es sich um eine Art von Frequency Shift Keying (FSK) mit kontinuierlicher Phasenanpassung $(\rm CP–FSK)$, bei der

der Modulationsindex kleinstmöglich ist, um die Orthogonalitätsbedingung noch zu erfüllen
$h = 0.5$ ⇒ Minimum Shift Keying,
ein Gaußtiefpass mit Impulsantwort $h_{\rm G}(t)$ vor dem FSK–Modulator eingebracht ist,
um noch weiter Bandbreite einzusparen.

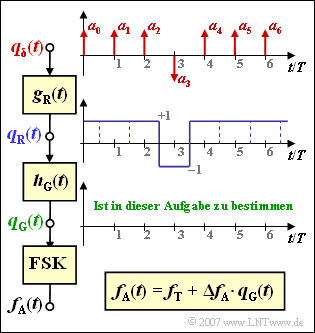
Die Grafik verdeutlicht den Sachverhalt:

Die digitale Nachricht wird durch die Amplitudenkoeffizienten $a_{\nu} ∈ ±1$ repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete (rote) Folge für die Teilaufgabe (3) vorausgesetzt wird.

Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer $T_{\rm B} = T$:

$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$

Damit ergibt sich für das Rechtecksignal:

$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$

Der Gaußtiefpass ist durch seinen Frequenzgang bzw. seine Impulsantwort gegeben:

$$H_{\rm G}(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}[f/(2 f_{\rm G})]^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$

wobei die systemtheoretische Grenzfrequenz $f_{\rm G}$ verwendet wird. In der GSM–Spezifikation wird aber die $3 \hspace{0.05cm}\rm dB$–Grenzfrequenz mit $f_{\rm 3\hspace{0.05cm} dB} = 0.3/T$ angegeben. Daraus kann $f_{\rm G}$ direkt berechnet werden.

Das Signal nach dem Gaußtiefpass lautet somit:

$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$

Hierbei wird $g(t)$ als Frequenzimpuls bezeichnet. Für diesen gilt:

$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$

Mit dem tiefpassgefilterten Signal $q_{\rm G}(t)$, der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $\Delta f_{\rm A}$ kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden:

$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$

Verwenden Sie für Ihre Berechnungen die beispielhaften Werte $f_{\rm T} = 900 \ \rm MHz$ und $\Delta f_{\rm A} = 68 \ \rm kHz$.

Hinweise:

Tabelle der Gaußschen Fehlerfunktion

Diese Aufgabe gehört zum Kapitel Funkschnittstelle.
Bezug genommen wird insbesondere auf die Seite Gaussian Minimum Shift Keying

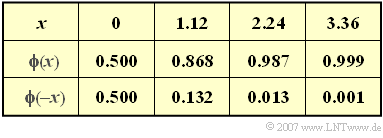
Verwenden Sie zur Lösung dieser Aufgabe das Gaußintegral (siehe nebenstehende Tabelle):

$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$

Fragebogen

${\rm Max} \ \big [f_{\rm A}(t) \big ] \ = \ $

$f_{\rm G} \cdot T \ = \ $

$g(t = 0) \ = \ $

$q_{\rm G}(t = 3T) \ = \ $

$ g(t = ±T) \ = \ $

${\rm Max} \ |q_{\rm G}(t)| \ = \ $

Musterlösung

(1) Wenn alle Amplitudenkoeffizienten $a_{\nu}$ gleich $+1$ sind, ist $q_{\rm R}(t) = 1$ eine Konstante.

Der Gaußtiefpass hat deshalb keinen Einfluss und es ergibt sich $q_{\rm G}(t) = 1$.
Die maximale Frequenz ist somit

$${\rm Max}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$

Das Minimum der Augenblicksfrequenz ergibt sich, wenn alle Amplitudenkoeffizienten negativ sind:

$${\rm Min}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$

In diesem Fall ist $q_{\rm R}(t) = q_{\rm G}(t) = -1$.

(2) Diejenige Frequenz, bei der die logarithmierte Leistungsübertragungsfunktion gegenüber $f = 0$ um $3 \ \rm dB$ kleiner ist, bezeichnet man als die $3\hspace{0.05cm}\rm dB$–Grenzfrequenz.

Diese lässt sich auch wie folgt ausdrücken:

$$\frac {|H(f = f_{\rm 3\hspace{0.05cm}dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$

Insbesondere gilt für den Gaußtiefpass wegen $H(f = 0) = 1$:

$$H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$

Die numerische Auswertung führt auf $f_{\rm G} \approx 1.5 \cdot f_{\rm 3\hspace{0.05cm}dB}$.
Aus $f_{\rm 3\hspace{0.05cm}dB} \cdot T = 0.3$ folgt somit $f_{\rm G} \cdot T \hspace{0.15cm}\underline{\approx 0.45}$.

(3) Der Frequenzimpuls ergibt sich aus der Faltung von Rechteckfunktion $g_{\rm R}(t)$ und Impulsantwort $h_{\rm G}(t)$:

$$g(t) = g_{\rm R} (t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot \int \limits^{t + T/2} _{t - T/2} {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot \tau)^2}\,{\rm d}\tau \hspace{0.05cm}.$$

Mit der Substitution $u^{2 } = 8π \cdot f_{\rm G}^{2} \cdot \tau^{2}$ und der Funktion $\phi (x)$ kann hierfür auch geschrieben werden:

$$g(t) \ = \ \frac {1}{\sqrt{2 \pi}} \cdot \int \limits^{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2)} _{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)} {\rm e}^{-u^2/2}\,{\rm d}u = \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2))- \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)) \hspace{0.05cm}.$$

Für die Zeit $t = 0$ gilt unter Berücksichtigung von $\phi (-x) = 1 - \phi (x)$ und $f_{\rm G} \cdot T = 0.45$:

$$g(t = 0) \ = \ \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(-\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)= 2 \cdot \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)-1 \approx 2 \cdot \phi(1.12)-1 \hspace{0.15cm} \underline {= 0.737} \hspace{0.05cm}.$$

(4) Mit $a_{3} = +1$ würde sich $q_{\rm G}(t = 3 T) = 1$ ergeben. Aufgrund der Linearität gilt somit:

$$q_{\rm G}(t = 3 T ) = 1 - 2 \cdot g(t = 0)= 1 - 2 \cdot 0.737 \hspace{0.15cm} \underline {= -0.474} \hspace{0.05cm}.$$

(5) Mit dem Ergebnis der Teilaufgabe (3) und $f_{\rm G} \cdot T = 0.45$ erhält man:

$$g(t = T) \ = \ \phi(3 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T) \approx \ \phi(3.36)-\phi(1.12) = 0.999 - 0.868 \hspace{0.15cm} \underline { = 0.131} \hspace{0.05cm}.$$

(6) Bei der alternierenden Folge sind aus Symmetriegründen die Beträge $|q_{\rm G}(\nu \cdot T)|$ bei allen Vielfachen der Bitdauer $T$ alle gleich.

Alle Zwischenwerte bei $t \neq \nu · T$ sind kleiner.
Unter Berücksichtigung von $g(t ≥ 2T) \approx 0$ wird jeder einzelne Impulswert $g(0)$ durch den vorangegangenen Impuls mit $g(t = T)$ verkleinert, zusätzlich vom nachfolgenden mit $g(t = -T)$.
Es ergeben sich also Impulsinterferenzen und man erhält:

$${\rm Max} \hspace{0.08cm}q_{\rm G}(t) = g(0) - 2 \cdot g(T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$