Aufgabe 2.4: Dualcodierung und Graycodierung

• Zurück zum Buch

Quaternärsignale mit Dual- und Graycodierung

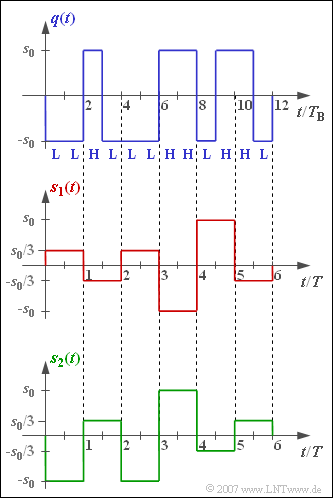
Die beiden dargestellten Signale $s_{1}(t)$ und $s_{2}(t)$ sind zwei unterschiedliche Realisierungen eines redundanzfreien quaternären Sendesignals, die beide vom blau gezeichneten Quellensignal $q(t)$ abgeleitet wurden. Bei einem der Sendesignale wurde der sog. Dualcode mit der Zuordnung

$$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$

verwendet, beim anderen eine bestimmte Form eines Graycodes. Dieser zeichnet sich dadurch aus, dass sich die Binärdarstellung benachbarter Amplitudenwerte immer nur in einem einzigen Bit unterscheiden.

Bei der Lösung der Aufgabe soll von folgenden Voraussetzungen ausgegangen werden:

• Die Amplitudenstufen liegen bei $±3\, \rm V$ und $±1 \, \rm V$.
• Die Entscheiderschwellen liegen in der Mitte zwischen zwei benachbarten Amplitudenwerten, also bei $–2\, \rm V$, $0\, \rm V$ und $+2\, \rm V$.
• Der Rauscheffektivwert $\sigma_{d}$ ist so zu wählen, dass die Verfälschungswahrscheinlichkeit vom äußeren Symbol $(+s_0)$ zum nächstgelegenen Symbol $(+s_{0}/3)$ genau $p = 1\%$ beträgt.
• Verfälschungen zu nicht benachbarten Symbolen können ausgeschlossen werden; bei Gaußschen Störungen ist diese Vereinfachung in der Praxis stets erlaubt.

Man unterscheidet grundsätzlich zwischen

• der Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ (bezogen auf das Quaternärsignal) und
• der Bitfehlerwahrscheinlichkeit $p_{B}$ (bezogen auf das binäre Quellensignal).

Hinweise:

• Die Aufgabe gehört zum Kapitel Grundlagen der codierten Übertragung.
• Bezug genommen wird auch auf das Kapitel Redundanzfreie Codierung .

• Zur numerischen Auswertung der Q–Funktion können Sie das interaktive Applet Komplementäre Gaußsche Fehlerfunktionen benutzen.

Fragebogen

1

Welches der Signale $s_{1}(t)$ bzw. $s_{2}(t)$ verwendet eine Graycodierung?

	$s_{1}(t)$ verwendet eine Graycodierung.
	$s_{2}(t)$ verwendet eine Graycodierung.

2

Bestimmen Sie den Rauscheffektivwert aus der angegebenen Bedingung.

$\sigma_{d} \ = \ $ $\ \rm V$

3

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem Graycode?

$p_{\rm S} \ = \ $ $\ \%$

4

Welche Bitfehlerwahrscheinlichkeit ergibt sich mit dem Graycode?

$p_{\rm B} \ = \ $ $\ \%$

5

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem Dualcode?

$p_{\rm S} \ = \ $ $\ \%$

6

Welche Bitfehlerwahrscheinlichkeit ergibt sich mit dem Dualcode?

$p_{\rm B} \ = \ $ $\ \%$

Musterlösung

Musterlösung

(1)  Im Signal $s_{2}(t)$ erkennt man die Realisierung des vorne angegebenen Dualcodes. Dagegen wurde beim Signal $s_{2}(t)$ ein Graycode $\Rightarrow$ Lösungsvorschlag 1 mit folgender Zuordnung verwendet:

$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$

(2)  Die Wahrscheinlichkeit $p$, dass der Amplitudenwert $3 \, \rm V$ aufgrund des gaußverteilten Rauschens mit der Streuung $\sigma_{d}$ die benachbarte Entscheiderschwelle $2\, \rm V$ unterschreitet, soll $1\, \%$ betragen. Daraus folgt:

$$p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$

(3)  Die beiden äußeren Symbole werden jeweils mit der Wahrscheinlichkeit $p$ verfälscht, die beiden inneren mit der doppelten Wahrscheinlichkeit $(2p)$. Durch Mittelung unter Berücksichtigung gleicher Symbolauftrittswahrscheinlichkeiten erhält man

$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$

(4)  Jeder Symbolfehler führt genau zu einem Bitfehler. Da jedoch jedes Quaternärsymbol genau zwei Binärsymbole beinhaltet, ergibt sich für die Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$

(5)  Bei der Berechnung der Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ wird das verwendete Mapping nicht berücksichtigt. Wie in der Teilaufgabe (3) erhält man somit $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$.

(6)  Die beiden äußeren Symbole werden mit $p$ verfälscht und führen auch beim Dualcode jeweils nur zu einem Bitfehler. Die inneren Symbole werden mit $2p$ verfälscht und führen nun im Mittel zu $1.5$ Bitfehlern. Unter Berücksichtigung des Faktors $2$ im Nenner – siehe Teilaufgabe (2) – erhält man somit für die Bitfehlerwahrscheinlichkeit des Dualcodes:

$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$