Attenuation of Copper Cables

Applet in neuem Tab öffnen

Theoretical Background

Magnitude Frequency Response and Attenuation Function

Following relationship exists between the magnitude frequency response and the attenuation function:

$$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$

• The index „K” makes it clear, that the considered LTI system is a cable(Ger: Kabel).
• For the first calculation rule, the damping function $a_\text{K}(f)$ must be used in $\rm dB$ (decibel).
• For the first calculation rule, the damping function $a_\text{K, Np}(f)$ must be used in $\rm Np$ (Neper).
• The following conversions apply: $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ or $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$.
• This applet exclusively uses dB values.

Attenuation Function of a Coaxial Cable

According to [Wel77] the Attenuation Function of a Coaxial Cable of length $l$ is given as follows:

$$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$

• It is important to note the difference between $a_{\rm K}(f)$ in $\rm dB$ and the „alpha” coefficient with other pseudo–units.
• The attenuation function $a_{\rm K}(f)$ is directly proportional to the cable length $l$; $a_{\rm K}(f)/l$ is referred to as the „attenuation factor” or „kilometric attenuation”.
• The frequency-independent component $α_0$ of the attenuation factor takes into account the Ohmic losses.
• The frequency proportional portion $α_1 · f$ of the attenuation factor is due to the derivation losses („crosswise loss”) .
• the dominant portion $α_2$ goes back to Skineffekt, which causes a lower current density inside the conductor compared to its surface. As a result, the resistance of an electric line increases with the square root of the frequency.

The constants for the standard coaxial cable with a 2.6 mm inner diameter and a 9.5 mm outer diameter   ⇒  short Coax (2.6/9.5 mm) are:

$$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$

The same applies to the coaxial coaxial cable'   ⇒  short Coax (1.2/4.4 mm):

$$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$

These values ​​can be calculated from the cables' geometric dimensions and have been confirmed by measurements at the Fernmeldetechnisches Zentralamt in Darmstadt – see [Wel77] . They are valid for a temperature of 20 ° C (293 K) and frequencies greater than 200 kHz.

Attenuation Function of a Two–wired Line

According to [PW95] the attenuation function of a Two–wired Line of length $l$ is given as follows:

$$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$

This function is not directly interpretable, but is a phenomenological description.

[PW95]also provides the constants determined by measurement results:

• $d = 0.35 \ {\rm mm}$:   $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$,
• $d = 0.40 \ {\rm mm}$:   $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$,
• $d = 0.50 \ {\rm mm}$:   $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$,
• $d = 0.60 \ {\rm mm}$:   $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$.

From these numerical values one recognizes:

• The attenuation factor $α(f)$ and the attenuation function $a_{\rm K}(f) = α(f) · l$ depend significantly on the pipe diameter. The cables laid since 1994 with $d = 0.35 \ \rm (mm)$ and $d = 0.5$ mm have a 10% greater attenuation factor than the older lines with $d = 0.4$ or $d= 0.6$.
• However, this smaller diameter, which is based on the manufacturing and installation costs, significantly reduces the range $l_{\rm max}$ of the transmission systems used on these lines, so that in the worst case scenario expensive intermediate generators have to be used.
• The current transmission methods for copper lines prove only a relatively narrow frequency band, for example $120\ \rm kHz$ with ISDN and ca. $1100 \ \rm kHz$ with DSL. For $f = 1 \ \rm MHz$ the attenuation factor of a 0.4 mm cable is around $20 \ \rm dB/km$, so that even with a cable length of $l = 4 \ \rm km$ the Attenuation does not exceed $80 \ \rm dB$.

Conversion Between $k$ and $\alpha$ parameters

The $k$–parameters of the attenuation factor   ⇒   $\alpha_{\rm I} (f)$ can be converted into corresponding $\alpha$–parameters   ⇒   $\alpha_{\rm II} (f)$:

$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$

$$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$

As a criterion of this conversion, we assume that the quadratic deviation of these two functions is minimal within a bandwidth $B$:

$$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$

It is obvious that $α_0 = k_1$. The parameters $α_1$ and $α_2$ are dependent on the underlying bandwidth $B$ and are:

$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$

$\text{Example 1:}$ 

• For $k_3 = 1$ (frequency proportional attenuation factor) we get   $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$
• For $k_3 = 0.5$ (Skin effect) we get the coefficients:   $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$
• For $k_3 < 0.5$ we get a negative $\alpha_1$. Conversion is only possible for $0.5 \le k_3 \le 1$.

Umrechnung in Gegenrichtung

Fehlt noch

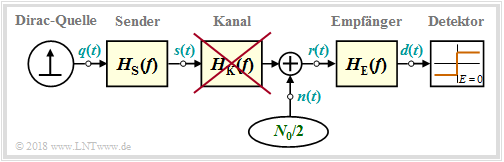
Channel Influence on the Binary Nyquistent Equalization

Simplified block diagram of the optimal Nyquistent equalizer

Going by the block diagram: Between the Dirac source and the decider are the frequency responses for the transmitter  ⇒  $H_{\rm S}(f)$, Channel  ⇒  $H_{\rm K}(f)$ and receiver   ⇒  $H_{\rm E}(f)$.

In this applet

• we neglect the influence of the transmitted pulse form   ⇒   $H_{\rm S}(f) \equiv 1$   ⇒   dirac shaped transmission signal $s(t)$,
• presuppose a binary Nyquist system with cosine–roll-off around the Nyquistf requency $f_{\rm Nyq} = [f_1 + f_2]/2 =1(2T)$ :

$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$

This means: The first Nyquist criterion is met  ⇒  
Timely successive impulses do not disturb each other   ⇒   there are no Intersymbol Interferences.

In the case of white noise, the transmission quality is thus determined solely by the noise power in front of the receiver:

$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$

The lowest possible noise performance results with an ideal channel   ⇒   $H_{\rm K}(f) \equiv 1$ and a rectangular $H_{\rm CRO}(f) \equiv 1$ in $|f| \le f_{\rm Nyq}$:

$$P_\text{N, min} = P_{\rm N} \ \big [\text{optimal system: }H_{\rm K}(f) \equiv 1, \ r=0 \big ] = N_0 \cdot f_{\rm Nyq} .$$

$\text{Definitionen:}$ 

• Als Gütekriterium für ein gegebenes System verwenden wir den Gesamt–Wirkungsgrad:

$$\eta_\text{K+R} = \frac{P_{\rm N} \ \big [\text{gegebenes System: Kanal }H_{\rm K}(f), \ \text{Roll-off-Faktor }r \big ]}{P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1, \ r=0 \big ]} =\frac{1}{f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \le 1.$$

Diese Systemgröße wird im Applet für beide Parametersätze in logarithmierter Form angegeben:   $10 \cdot \lg \ \eta_\text{K+R} \le 0 \ \rm dB$.

• Durch Variation und Optimierung des Roll-off-Faktors $r$ erhält man den Kanal–Wirkungsgrad:

$$\eta_\text{K} = \min_{0 \le r \le 1} \ \eta_\text{K+R} .$$

Ab hier bis zum Beginn der Versuchsdurchführung ist alles Mist - eine Art Vorratsspeicher

• Bei UMTS ist das Empfangsfilter $H_{\rm E}f) = H_{\rm S}(f)$ an den Sender angepasst (Matched–Filter) und der Gesamtfrequenzgang $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt

$$H(f) = H_{\rm CRO}(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \cos^2 \left( \frac {\pi \cdot (|f| - f_1)}{2 \cdot (f_2 - f_1)} \right)\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm sonst }\hspace{0.05cm}. \end{array} \begin{array}{*{20}c} |f| \le f_1, \\ |f| \ge f_2,\\ \\\end{array}$$

Die zugehörige Zeitfunktion lautet:

$$h(t) = h_{\rm CRO}(t) ={\rm si}(\pi \cdot t/ T_{\rm C}) \cdot \frac{\cos(r \cdot \pi t/T_{\rm C})}{1- (2r \cdot t/T_{\rm C})^2}.$$

„CRO” steht hierbei für Cosinus–Rolloff (englisch: Raised Cosine). Die Summe $f_1 + f_2$ ist gleich dem Kehrwert der Chipdauer $T_{\rm C} = 260 \ \rm ns$, also gleich $3.84 \ \rm MHz$. Der Rolloff–Faktor (wir bleiben bei der in $\rm LNTwww$ gewählten Bezeichnung $r$, im UMTS–Standard wird hierfür $\alpha$ verwendet)

$$r = \frac{f_2 - f_1}{f_2 + f_1}$$

wurde bei UMTS zu $r = 0.22$ festgelegt. Die beiden Eckfrequenzen sind somit

$$f_1 = {1}/(2 T_{\rm C}) \cdot (1-r) \approx 1.5\,{\rm MHz}, \hspace{0.2cm} f_2 ={1}/(2 T_{\rm C}) \cdot (1+r) \approx 2.35\,{\rm MHz}.$$

Die erforderliche Bandbreite beträgt $B = 2 · f_2 = 4.7 \ \rm MHz$. Für jeden UMTS–Kanal steht somit mit $5 \ \rm MHz$ ausreichend Bandbreite zur Verfügung.

Cosinus–Rolloff–Spektrum und Impulsantwort

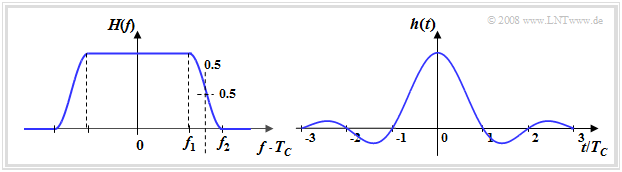
$\text{Fazit:}$  Die Grafik zeigt

• links das (normierte) Nyquistspektrum $H(f)$, und
• rechts den zugehörigen Nyquistimpuls $h(t)$, dessen Nulldurchgänge im Abstand $T_{\rm C}$ äquidistant sind.

$\text{Es ist zu beachten:}$

• Das Sendefilter $H_{\rm S}(f)$ und Matched–Filter $H_{\rm E}(f)$ sind jeweils Wurzel–Cosinus–Rolloff–förmig (englisch: Root Raised Cosine). Erst das Produkt $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ den Cosinus–Rolloff.
• Das bedeutet auch: Die Impulsantworten $h_{\rm S}(t)$ und $h_{\rm E}(t)$ erfüllen für sich allein die erste Nyquistbedingung nicht. Erst die Kombination aus beiden (im Zeitbereich die Faltung) führt zu den gewünschten äquidistanten Nulldurchgängen.

$$a_k(f)=(k_1+k_2\cdot f^{k_3})\cdot l \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \text{empirische Formel von Pollakowski & Wellhausen.}$$

• Umrechnung der $k$-Parameter in die $a$-Parameter nach dem Kriterium, dass der mittlere quadratische Fehler innerhalb der Bandbreite $B$ minimal sein soll:

$$a_0=k_1 \text{(trivial)}, \quad a_1=15\cdot B^{k_3-1}\cdot \frac{k_2\cdot (k_3-0.5)}{(k_3+1.5)\cdot (k_3+2)}, \quad a_2=10\cdot B^{k_3-0.5}\cdot \frac{k_2\cdot (1-k_3)}{(k_3+1.5)\cdot (k_3+2)}.$$

• Kontrolle: $k_3=1 \Rightarrow a_1=k_2;\ a_2=0 \quad k_3=0.5 \Rightarrow a_1=0;\ a_2=k_2.$
• Der Gesamtfrequenzgang $H(f)$ ist ein Cosinus-Rolloff-Tiefpass mit Rolloff-Faktor $r$, wobei stets $B=f_2$ und $r=\frac{f_2-f_1}{f_2+f_1}$ gelten soll.
• Ohne Berücksichtigung des Sendespektrums gilt $H(f)=H_K(f)\cdot H_E(f) \Rightarrow H_E(f)=\frac{H(f)}{H_K(f)}$.
• Der angegebene Integralwert $=\int_{-\infty}^{+\infty} \left| H_E(f)\right|^2 \hspace{0.15cm} {\rm d}f$ ist ein Maß für die Rauschleistung des Systems, wenn der Kanal $H_K(f)$ durch das Empfangsfilter $H_E(f)$ in weiten Bereichen bis $f_1$ vollständig entzerrt wird.

• idealer Kanal ($a_0=a_1=a_2=0$ dB), $B=20$ MHz, $r=0$: Integralwert = $40$ MHz.
• schwach verzerrender Kanal ($a_2=5$ dB), $B=20$ MHz, $r=0.5$: Integralwert $\approx 505$ MHz.

Exercises

• First choose an exercise number.
• An exercise description is displayed.
• Parameter values are adjusted to the respective exercises.
• Click „Hide solition” to display the solution.
• Exercise description and solution in english

Number „0” is a „Reset” button:

• Sets parameters to initial values (when loading the page).
• Displays a „Reset text” to describe the applet further.

In der folgenden Beschreibung bedeutet

• Blau:   Verteilungsfunktion 1 (im Applet blau markiert),
• Rot:     Verteilungsfunktion 2 (im Applet rot markiert).

(1)  First set Blue to $\text{Coax (2.6/9.5 mm)}$ and then to $\text{Coax (1.2/4.4 mm)}$. The cable length is $l_{\rm Blue}= 3\ \rm km$.

Interpret $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$, in particular the functional values $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ and $\vert H_{\rm K}(f = 0) \vert$.

$\Rightarrow\hspace{0.3cm}\text{The attenuation function increases approximately }\sqrt{f}\text{ and the magnitude frequency response falls similarly to an exponential function};$

$\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 39.2\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.9951;$

$\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 86.0\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.9768.$

(2)  Set Blue to $\text{Coax (1.2/4.4 mm)}$ and $l_{\rm Blue} = 3\ \rm km$. How is $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ affected by $\alpha_0$, $\alpha_1$ und $\alpha_2$?

$\Rightarrow\hspace{0.3cm}\alpha_2\text{is crucial (Skin effect). The contributions of } \alpha_0\text{ (Ohmic losses) and }\alpha_1 \text{ (crosswise losses) are only ca. 0.2 dB respectively.}$

(3)  Additionally, set Red to $\text{Two–wired Line (0.5 mm)}$ and $l_{\rm Red} = 3\ \rm km$. What is the resulting value for $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$?

Up to what length $l_{\rm Red}$ does the red attenuation function go under the blue one?

$\Rightarrow\hspace{0.3cm}\text{Red curve: }a_{\rm K}(f = f_\star) = 262.5 {\ \rm dB} \text{. The above condition is fulfilled for }l_{\rm Red} = 0.95\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = ??? {\ \rm dB}.$

(4)  Set Red to $\text{Two–wired Line (0.5 mm)}$ and Blue to $\text{Conversion of Red}$. For the length use $l_{\rm Rot} = l_{\rm Blau} = 1\ \rm km$.

Analyse and interpret the displayed functions $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$.

$\Rightarrow\hspace{0.3cm}\text{Very good approximation of the two-wire line through the blue parameter set, both with regard to }a_{\rm K}(f) \text{, as well as }\vert H_{\rm K}(f) \vert.$

(5)  We assume the settings of (4). Which parts of the attenuation function are due to ohmic loss, lateral losses and skin effect?

$\Rightarrow\hspace{0.3cm}\text{Solution based on '''Blue''': }\alpha_0(f = f_\star= 30 \ {\rm MHz}) = 4 \ {\rm dB/km}, \hspace{0.2cm}\alpha_1(f = f_\star) = 12.8 \ {\rm dB/km}, \hspace{0.2cm}\alpha_2(f = f_\star) = 60.9 \ {\rm dB/km};$

$\hspace{1.15cm}\text{With a two-wire cable, the influence of the longitudinal and transverse losses is significantly greater than with a coaxial cable.}$

(6)  Based on the previous setting, vary the parameter $0.5 \le k_3 \le 1$. What do you recognize by means of $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$?

$\Rightarrow\hspace{0.3cm}\text{At constant }k_2\text { }a_{\rm K}(f)\text{ becomes increasingly larger and has a linear coursse for }k_3 = 1;\text{ }\vert H_{\rm K}(f) \vert \text{ decreases at an increasing rate;}$

$\hspace{1.15cm}\text{At }k_3 \to 0.5\text{ The attenuation function of the two-wire line approaches that of a coaxial cable more and more.}$

Vorgeschlagene Parametersätze

(1)   Nur blauer Parametersatz, $l=1$ km, $B=30$ MHz, $r=0$, $a_0=20$, $a_1=0$, $a_2=0$:
Konstante Werte $a_K=20$ dB und $\left| H_K(f)\right|=0.1$. Nur Ohmsche Verluste werden berücksichtigt.
(2) Parameter wie (1), aber zusätzlich $a_1=1$ dB/(km · MHz):
Linearer Anstieg von $a_K(f)$ zwischen $20$ dB und $50$ dB, $\left| H_K(f)\right|$ fällt beidseitig exponentiell ab.
(3)   Parameter wie (1), aber $a_0=0$, $a_1=0$, $a_2=1$ dB/(km · MHz^1/2).
$a_K(f)$ und $\left| H_K(f)\right|$ werden ausschließlich durch den Skineffekt bestimmt. $a_K(f)$ ist proportional zu $f^{1/2}$.
(4)   Parameter wie (1), aber nun mit der Einstellung „Koaxialkabel $2.6/9.5$ mm“ (Normalkoaxialkabel):
Es überwiegt der Skineffekt; $a_k$ ($f=30$ MHz)$=13.05$ dB; ohne $a_0$: $13.04$ dB, ohne $a_1=12.92$ dB.
(5)   Parameter wie (1), aber nun mit der Einstellung „Koaxialkabel $1.2/4.4$ mm“ (Kleinkoaxialkabel):
Wieder überwiegt der Skineffekt; $a_k$ ($f=30$ MHz)$=28.66$ dB; ohne $a_0$: $28.59$ dB, ohne $a_1=28.48$ dB.
(6)   Nur roter Parametersatz, $l=1 km$, $b=30$ MHz, $r=0$, Einstellung „Zweidrahtleitung $0.4$ mm“.
Skineffekt ist auch hier dominant; $a_k$ ($f=30$ MHz)$=111.4$ dB; ohne $k_1$: $106.3$ dB.
(7)   Parameter wie (6), aber nun Halbierung der Kabellänge ($l=0.5$ km):
Auch die Dämpfungswerte werden halbiert: $a_k$ ($f=30$ MHz)$=55.7$ dB; ohne $k_1$: $53.2$ dB.
(8)   Parameter wie (7), dazu im blauen Parametersatz die umgerechneten Werte der Zweidrahtleitung:
Sehr gute Approximation der $k$-Parameter durch die $a$-Parameter; Abweichung < $0.4$ dB.
(9)   Parameter wie (8), aber nun Approximation auf die Bandbreite $B=20$ MHz:
Noch bessere Approximation der $k$-Parameter durch die $a$-Parameter; Abweichung < $0.15$ dB.
(10)   Nur blauer Parametersatz, $l=1$ km, $B=30$ MHz, $r=0$, $a_0=a_1=a_2=0$; unten Darstellung $\left| H_K(f)\right|^2$:
Im gesamten Bereich ist $\left| H_K(f)\right|^2=1$; der Integralwert ist somit $2B=60$ (in MHz).
(11)   Parameter wie (10), aber nun mit Einstellung „Koaxialkabel $2.6/9.5$ mm“ (Normalkoaxialkabel):
$\left| H_K(f)\right|^2$ ist bei $f=1$ etwa $1$ und steigt zu den Rändern bis ca. $20$. Der Integralwert ist ca. $550$.
(12)   Parameter wie (11), aber nun mit der deutlich größeren Kabellänge $l=5$ km:
Deutliche Verstärkung des Effekts; Anstieg bis ca. $3.35\cdot 10^6$ am Rand und Integralwert $2.5\cdot 10^7$.
(13)   Parameter wie (12), aber nun mit Rolloff-Faktor $r=0.5$:
Deutliche Abschwächung des Effekts; Anstieg bis ca. $5.25\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $1.07\cdot 10^6$.
(14)   Parameter wie (13), aber ohne Berücksichtigung der Ohmschen Verluste ($a_0=0$):
Nahezu gleichbleibendes Ergebnis; Anstieg bis ca. $5.15\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $1.05\cdot 10^6$.
(15)   Parameter wie (14), aber auch ohne Berücksichtigung der Querverluste ($a_1=0$):
Ebenfalls kein großer Unterschied; Anstieg bis ca. $4.74\cdot 10^4$ ($f$ ca. $20$ MHz), Integralwert ca. $0.97\cdot 10^6$.
(16)   Nur roter Parametersatz, $l=1$ km, $B=30$ MHz, $r=0.5$, Einstellung „Zweidrahtleitung $0.4$ mm“:
Anstieg bis ca. $3\cdot 10^8$ ($f$ ca. $23$ MHz), Integralwert ca. $4.55\cdot 10^9$; ohne $k_1$: $0.93\cdot 10^8$ ($f$ ca. $23$ MHz) bzw. $1.41\cdot 10^9$.

Quellenverzeichnis

Applet in neuem Tab öffnen