Linear Distortions of Periodic Signals
Inhaltsverzeichnis
Applet description
This applet illustrates the effects of linear distortions (attenuation distortions and phase distortions) with
- the input signal x(t) ⇒ power Px:
- x(t)=x1(t)+x2(t)=A1⋅cos(2πf1⋅t−φ1)+A2⋅cos(2πf2⋅t−φ2),
- the output signal y(t) ⇒ power Py:
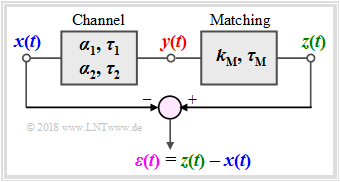
- y(t)=α1⋅x1(t−τ1)+α2⋅x2(t−τ2),
- the matching output signal z(t) ⇒ power Pz:
- z(t)=kM⋅y(t−τM)+α2⋅x2(t−τ2),
- the difference signal ε(t)=z(t)−x(t) ⇒ power Pε.
The next block in the above model is Matching: The output signal y(t) is adjusted in amplitude and phase with uniform quantities kM and τM for all frequencies which means that this is not a frequency-dependent distortion. Using the signal z(t), a differentiation can be made between:
- attenuation distortion and frequency–independant attenuation, as well as
- phase distortion and pure frequency–independant delay.
The Distortion Power PD is used to measure the strength of the linear distortion and is defined as:
- PD=minkM, τMPε.
Theoretical background
Distortions refer to generally unwanted alterations of a message signal through a transmission system. Together with the strong stochastic effects (noise, crosstalk, etc.), they are a crucial limitation for the quality and rate of transmission.
Just as the intensity of noise can be assessed through
- the Noise Power PN and
- the Signal–to–Noise Ratio (SNR) ρN,
distortions can be quantified through
- the Distortion Power PD and
- the Signal–to–Distortion Ratio (SDR)
- ρD=Signal PowerDistortion Power=PxPD.
Linear and nonlinear distortions
A distinction is made between linear and nonlinear distortions:
- Nonlinear distortions occur, if at all times t the nonlinear correlation y=g(x)≠const.⋅x exists between the signal values x=x(t) at the input and y=y(t) at the output, whereby y=g(x) is defined as the system's nonlinear characteristic. By creating a cosine signal at the input with frequency f0 the output signal includes f0 as well as multiple harmonic waves. We conclude that new frequencies arise through nonlinear distortion.
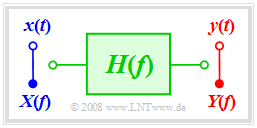
- Linear distortions occur, if the transmission channel is characterized by a frequency response H(f)≠const. Various frequencies are attenuated and delayed differently. Characteristic of this is that although frequencies can disappear (for example, through a low–pass, a high–pass, or a band–pass), no new frequencies can arise.
In this applet only linear distortions are considered.
Description forms for the frequency response
The generally complex valued frequency response can be represented as follows:
- H(f)=|H(f)|⋅e−j⋅b(f)=e−a(f)⋅e−j⋅b(f).
This results in the following description variables:
- The absolute value |H(f)| is called amplitude response and in logarithmic form attenuation function:
- a(f)=−ln|H(f)|inNeper(Np)=−20⋅lg|H(f)|inDecibel(dB).
- The phase function b(f) indicates the negative frequency–dependent angle of H(f) in the complex plane based on the real axis:
- b(f)=−arcH(f)inRadian(rad).
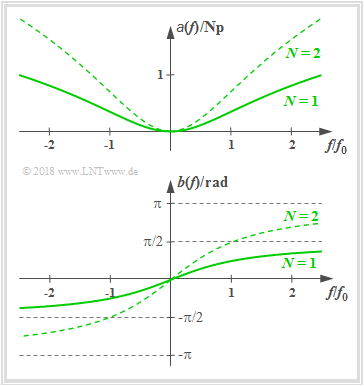
Low–pass of order N
The frequency response of a realizable low–pass (LP) of order N is:
- H(f)=[11+j⋅f/f0]N.
For example the RC low–pass is a first order low–pass. Consequently we can obtain
- the attenuation function:
- a(f)=N/2⋅ln[1+(f/f0)2],
- the phase function:
- b(f)=N⋅arctan(f/f0),
- the attenuation factor for the frequency f=fi:
- αi=|H(f=fi)|=[1+(fi/f0)2]−N/2
- ⇒x(t)=Ai⋅cos(2πfit)→y(t)=αi⋅Ai⋅cos(2πfit),
- the phase delay for the frequency f=fi:
- τi=b(fi)2πfi=N⋅arctan(fi/f0)2πfi
- ⇒x(t)=Ai⋅cos(2πfit)→y(t)=Ai⋅cos(2πfi(t−τi)).
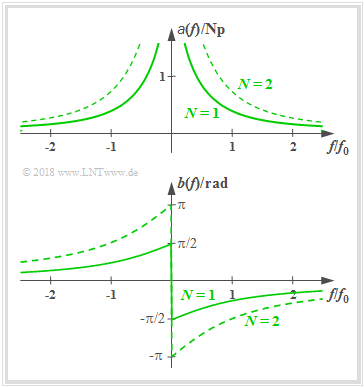
High–pass of order N
The frequency response of a realizable high–pass (HP) of order N is:
- H(f)=[j⋅f/f01+j⋅f/f0]N.
For example the LC high pass is a first grade high pass. Consequently we can obtain
- the attenuation function:
- a(f)=N/2⋅ln[1+(f0/f)2],
- the phase function:
- b(f)=−N⋅arctan(f0/f),
- the attenuation factor for the frequency f=fi:
- αi=|H(f=fi)|=[1+(f0/fi)2]−N/2
- ⇒x(t)=Ai⋅cos(2πfit)→y(t)=αi⋅Ai⋅cos(2πfit),
- the phase delay for the frequency f=fi:
- τi=b(fi)2πfi=−N⋅arctan(f0/fi)2πfi
- ⇒x(t)=Ai⋅cos(2πfit)→y(t)=Ai⋅cos(2πfi(t−τi)).
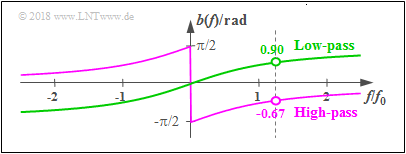
Example: This graphic shows the phase function b(f) with the cut–off frequency f0=1 kHz and order N=1
- of a low–pass (green curve),
- of a high–pass (violet curve).
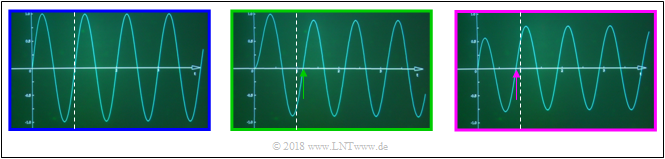
The input signal is sinusoidal with frequency fS=1.25 kHz whereby this signal is only turned on at t=0:
- x(t)={0sin(2π⋅fS⋅t)(t<0),(t>0).
The left graphic shows the signal x(t). The dashed line marks the first zero at t=T0=0.8 ms. The other two graphics show the output signals yLP(t) und yHP(t) of low–pass and high–pass, whereby the change in amplitude was balanced in both cases.
- The first zero of the signal yLP(t) after the low–pass is delayed by τLP=0.9/(2π)⋅T0≈0.115 ms compared to the first zero of x(t) ⇒ marked with green arrow, whereby bLP(f/fS=0.9 rad) was considered.
- In contrast, the phase delay of the high–pass is negative: τHP=−0.67/(2π)⋅T0≈−0.085 ms and therefore the first zero of yHP(t) occurs before the dashed line.
- Following this transient response, in both cases the zero crossings again come in the raster of the period duration T0=0.8 ms.
Annotation: The shown signals were created using the interactive applet Causal systems – Laplace transform.
Attenuation distortions and phase distortions
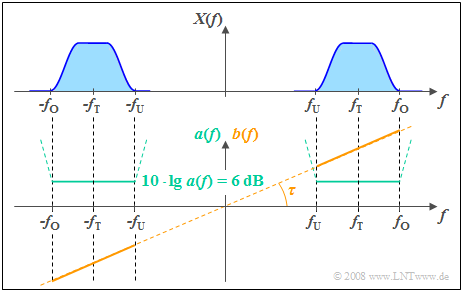
The adjacent figure shows
- the even attenuation function a(f) ⇒ a(−f)=a(f), and
- the uneven function curve b(f) ⇒ b(−f)=−b(−f)
of a non–distorting channel. One notices:
- In a distortion–free system the attenuation function a(f) must be constant betweenfU and fO around the carrier frequency fT, where the input signal exist ⇒ x(t)≠0.
- From the specified constant attenuation value 6 dB follows for the amplitude response |H(f)|=0.5 ⇒ the signal values of all frequencies are thus halved by the system ⇒ no attenuation distortions.
- In addition, in such a system, the phase function b(f) between fU and fO must increase linearly with the frequency. As a result, all frequency components are delayed by the same phase delay τ ⇒ no phase delay.
- The delay τ is fixed by the slope of b(f). The phase function b(f) \equiv 0 would result in a delay–less system ⇒ τ = 0.
The following summary considers that in this applet the input signal is always the sum of two harmonic oscillations,
- x(t) = x_1(t) + x_2(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right),
and therefor the channel influence is fully described by the attenuation factors \alpha_1 and \alpha_2 as well as the phase delays \tau_1 and \tau_2:
- y(t) = \alpha_1 \cdot x_1(t-\tau_1) + \alpha_2 \cdot x_2(t-\tau_2).
\text{Summary:}
- A signal y(t) is only distortion–free compared to x(t) if \alpha_1 = \alpha_2= \alpha and \tau_1 = \tau_2= \tau ⇒ y(t) = \alpha \cdot x(t-\tau).
- Attenuation distortions occur when \alpha_1 \ne \alpha_2. If \alpha_1 \ne \alpha_2 and \tau_1 = \tau_2, then there are exclusively attenuation distortions.
- Phase distortions occur when \tau_1 \ne \tau_2. If \tau_1 \ne \tau_2 and \alpha_1 = \alpha_2, then there are exclusively phase distortions.
Exercises
BlaBla
(1) We set the parameters for the Input signal x(t) to A_1 = 0.8\ {\rm V}, \ A_2 = 0.6\ {\rm V}, \ f_1 = 0.5\ {\rm kHz}, \ f_2 = 1.5\ {\rm kHz}, \ \varphi_1 = 90^\circ, \ \varphi_2 = 30^\circ.
- Calculate the signal's cycle duration T_0 and power P_x. Can you read the value for P_x off the applet?
\hspace{1.0cm}\Rightarrow\hspace{0.3cm}T_0 = \big [\hspace{-0.1cm}\text{ greatest common divisor }(0.5 \ {\rm kHz}, \ 1.5 \ {\rm kHz})\big ]^{-1}\hspace{0.15cm}\underline{ = 2.0 \ {\rm ms}};
\hspace{1.85cm} P_x = A_1^2/2 + A_2^2/2 \hspace{0.15cm}\underline{= 0.5 \ {\rm V^2}} = P_\varepsilon\text{, if }\hspace{0.15cm}\underline{k_{\rm M} = 0} \ \Rightarrow \ z(t) \equiv 0.
(2) Vary \varphi_2 between \pm 180^\circ while assuming the other parameters from Exercise '''(1)'''. How does the value of T_0 and P_x change?
\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{No changes:}\hspace{0.2cm}\hspace{0.15cm}\underline{ T_0 = 2.0 \ {\rm ms}; \hspace{0.2cm} P_x = 0.5 \ {\rm V^2}}.
(3) Vary f_2 between 0 \le f_2 \le 10\ {\rm kHz} while assuming the other parameters from Exercise '''(1)'''. How does the value of P_x change?
\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{No changes if }f_2 \ne 0\text{ oder } f_2 \ne f_1\text{:}\hspace{0.3cm} \hspace{0.15cm}\underline{P_x = 0.5 \ {\rm V^2}}\text{.} \hspace{0.2cm} T_0 \text{ changes if }f_2\text{is not a multiple of }f_1.
\hspace{1.85cm}\text{If }f_2 = 0\text{:}\hspace{0.2cm} P_x = A_1^2/2 + A_2^2\hspace{0.15cm}\underline{ = 0.68 \ {\rm V^2}}. \hspace{3cm}
\hspace{1.85cm}\text{If }f_2 = f_1\text{:}\hspace{0.2cm} P_x = [A_1\cos(\varphi_1) + A_2\cos(\varphi_2)]^2/2 + [A_1\sin(\varphi_1) + A_2\sin(\varphi_2)]^2/2 \text{.}
\hspace{1.85cm}\text{Mit } \varphi_1 = 90^\circ, \ \varphi_2 = 30^\circ\text{:}\hspace{0.3cm}\hspace{0.15cm}\underline{ P_x = 0.74 \ {\rm V^2}}\text{.}
(4) Going by the previous output signal x(t) we set following parameters to: \alpha_1 = \alpha_2 = 0.5, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}, k_{\rm M} = 1 \text{ and } \tau_{\rm M} = 0 .
- Are there linear distortions? Calculate the reception power P_y and the power P_\varepsilon of the differential signal \varepsilon(t) = z(t) - x(t).
\hspace{1.0cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{ y(t) = 0.5 \cdot x(t- 1\ {\rm ms})}\text{ is only attenuated and delayed, but not distorted.}
\hspace{1.85cm}\text{Reception power:}\hspace{0.2cm} P_y = (A_1/2)^2/2 + (A_2/2)^2/2\hspace{0.15cm}\underline{ = 0.125 \ {\rm V^2}}\text{. } P_\varepsilon \text{ is significantly greater:} \hspace{0.1cm} \hspace{0.15cm}\underline{P_\varepsilon = 0.625 \ {\rm V^2}}.
(5) With otherwise the same settings as In exercise '''(4)''', vary the matching parameters k_{\rm M} \text{ and } \tau_{\rm M}. How big is the distortion power P_{\rm D}?
\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D}\text{is equal to }P_\varepsilon \text{ when using the ideal matching parameters:} \hspace{0.2cm}k_{\rm M} = 2 \text{ und } \tau_{\rm M}=T_0 - 0.5\ {\rm ms} = 1.5\ {\rm ms}
\hspace{1.0cm}\Rightarrow \hspace{0.3cm}z(t) = x(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\varepsilon(t) = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm D}\hspace{0.15cm}\underline{ = P_\varepsilon = 0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{Neither attenuation nor phase distortion.}
(6) The channel parameters are now set to: \alpha_1 = 0.5, \hspace{0.15cm}\underline{\alpha_2 = 0.2}, \ \tau_1 = \tau_2 = 0.5\ {\rm ms}. Calculate the distortion power P_{\rm D} and The Signal-to-Distortion ratio (\rm SDR) \ \rho_{\rm D}.
\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{ when using the best matching parameters:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 2.24} \text{ und } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.5\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.059 \ {\rm V^2}}.
\hspace{1.85cm}\text{Attenuation distortions only.} \hspace{0.3cm}\text{Signal-to-Distortion-Ratio}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 8.5}.
(7) The channel parameters are now set to: \alpha_1 = \alpha_2 = 0.5, \ \tau_1 \hspace{0.15cm}\underline{= 2\ {\rm ms} }, \ \tau_2 = 0.5\ {\rm ms}. Calculate the distortion power P_{\rm D} and the SDR \rho_{\rm D}?
\hspace{1.0cm}\Rightarrow \hspace{0.3cm} P_{\rm D} = P_\varepsilon \text{when using the best matching parameters:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.84} \text{ and } \tau_{\rm M}\hspace{0.15cm}\underline{ = 0.15\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.071 \ {\rm V^2}}.
\hspace{1.85cm}\text{Phase distortions only.} \hspace{0.3cm}\text{Signal-to-Distortion-Ratio}\ \hspace{0.15cm}\underline{\rho_{\rm D} = P_x/P_\varepsilon \approx 7}.
(8) The channel parameters are now set to: \hspace{0.15cm}\underline{\alpha_1 = 0.5} , \hspace{0.15cm}\underline{\alpha_2 = 0.2} , \ \hspace{0.15cm}\underline{\tau_1= 0.5\ {\rm ms} }, \ \hspace{0.15cm}\underline{\tau_2 = 0.3\ {\rm ms} }. Are there attenuation distortions? Are there phase distortions? How can y(t) be approximated? How can y(t) be approximated? Annotation: \cos(3x) = 4 \cdot \cos(x)^3 - 3\cdot \cos(x).
\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Both attenuation and phase distortions, because }\alpha_1 \ne \alpha_2\text{ and }\tau_1 \ne \tau_2.
\hspace{1.85cm}y(t) = y_1(t) + y_2(t)\ \Rightarrow \ y_1(t) = A_1 \cdot \alpha_1 \cdot \sin[2\pi f_1\ (t- 0.5\ \rm ms)] = -0.4 \ {\rm V} \cdot \cos(2\pi f_1 t)
\hspace{1.85cm} y_2(t) = \alpha_2 \cdot x_2(t- \tau_2) \text{ mit }x_2(t) = A_2 \cdot \cos[2\pi f_2\ (t- 30^\circ)] \approx A_2 \cdot \cos[2\pi f_2\ (t- 1/36 \ \rm ms)]
\hspace{1.85cm} \Rightarrow \ y_2(t) = 0.12 \ {\rm V} \cdot \cos[2\pi f_2\ (t- 0.328 \ {\rm ms})] \approx -0.12 \ { \rm V} \cdot \cos[2\pi f_2t] .
\hspace{1.85cm} \Rightarrow \ y(t) = y_1(t) + y_2(t) \approx -0.4 \ {\rm V} \cdot [\cos(2\pi \cdot f_1\cdot t) + 1/3 \cdot \cos(2\pi \cdot 3 f_1 \cdot t) = -0.533 \ {\rm V} \cdot \cos^3(2\pi f_1 t).
(9) Assuming the parameters from 88Exercize (8)]]. Calculate the distortion power P_{\rm D} and the SDR \rho_{\rm D}?
\hspace{1.0cm}\text{Best possible adaptation:} \hspace{0.2cm}\hspace{0.15cm}\underline{k_{\rm M} = 1.96} \text{, } \hspace{0.15cm}\underline{\tau_{\rm M} = 1.65\ {\rm ms} }\text{:} \hspace{0.2cm}\hspace{0.15cm}\underline{P_{\rm D} = 0.156 \ {\rm V^2} },\hspace{0.1cm}\hspace{0.15cm}\underline{\rho_{\rm D} = 0.500/0.156 \approx 3.2}.
(10) Now we set A_2 = 0 and A_1 = 1\ {\rm V}, \ f_1 = 1\ {\rm kHz}, \ \varphi_1 = 0^\circ. The channel is a Low-pass of order 1 \underline{(f_0 = 1\ {\rm kHz})}.
Are there any attenuation or phase distortions? Calculate the channel coefficients \alpha_1 and \tau_1
\hspace{1.0cm}\text{At only one frequency there are neither attenuation nor phase distortions.}
\hspace{1.0cm}\text{Attenuation factor for }f_1=f_0\text{ and }N=1\text{: }\alpha_1 =|H(f = f_1)| = [1+( f_1/f_0)^2]^{-N/2} = 2^{-1/2}= 1/\sqrt{2}\hspace{0.15cm}\underline{=0.707},
\hspace{1.0cm}\text{Phase factor for }f_1=f_0\text{ and }N=1\text{: }\tau_1 = N \cdot \arctan( f_1/f_0)/(2 \pi f_i)=\arctan( 1)/(2 \pi f_i) =1/(8f_1) \hspace{0.15cm}\underline{=0.125 \ \rm ms}.
Zur Handhabung des Applets
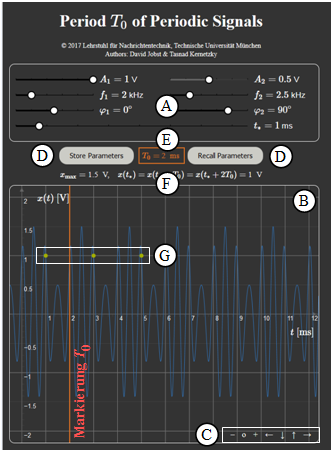
(A) Parametereingabe per Slider
(B) Bereich der graphischen Darstellung
(C) Variationsmöglichkeit für die graphische Darstellung
(D) Abspeichern und Zurückholen von Parametersätzen
(E) Numerikausgabe des Hauptergebnisses T_0; graphische Verdeutlichung durch rote Linie
(F) Ausgabe von x_{\rm max} und der Signalwerte x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)
(G) Darstellung der Signalwerte x(t_*) = x(t_* + T_0)= x(t_* + 2T_0) durch grüne Punkte
(H) Einstellung der Zeit t_* für die Signalwerte x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)
Details zum obigen Punkt (C)
(*) Zoom–Funktionen „+” (Vergrößern), „-” (Verkleinern) und \rm o (Zurücksetzen)
(*) Verschieben mit „\leftarrow” (Ausschnitt nach links, Ordinate nach rechts), „\uparrow” „\downarrow” und „\rightarrow”
Andere Möglichkeiten:
(*) Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
(*) Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder ).
- 2018 wurde dieses Programm von Jimmy He im Rahmen seiner Bachelorarbeit (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.