Aufgabe 2.7: AMI-Code
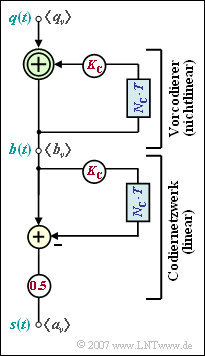
Die Grafik zeigt das Blockschaltbild zur AMI–Codierung, wobei von den binären bipolaren Amplitudenkoeffizienten qν∈{–1,+1} am Eingang ausgegangen wird. Diese Umcodierung erfolgt zweistufig:
- Im ersten Teil des Blockschaltbildes wird bei jedem Taktschritt ein binär–vorcodiertes Symbol bν aus der Modulo–2–Addition von qν und bν−1 erzeugt. Es gilt bν∈{–1,+1}.
- Danach wird durch eine herkömmliche Subtraktion der aktuelle Amplitudenkoeffizient des ternären Sendesignals s(t) bestimmt. Dabei gilt:
- aν=1/2⋅[bν−bν−1].
Aufgrund der AMI–Codierung wird sichergestellt, dass keine langen „+1”– bzw. „–1”–Sequenzen entstehen. Um auch lange Nullfolgen zu vermeiden, wurden auch modifizierte AMI–Codes entwickelt:
- Beim HDB3–Code werden je vier aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.
- Beim B6ZS–Code werden sechs aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.
Das Leistungsdichtespektrum Φa(f) der Amplitudenkoeffizienten soll aus den diskreten AKF–Werten φa(λ)=E[aν⋅aν+λ] ermittelt werden. Die Fouriertransformation lautet in diskreter Darstellung:
- Φa(f)=+∞∑λ=−∞φa(λ)⋅e−j2πfλT.
Hinweise:
- Die Aufgabe gehört zum Kapitel Symbolweise Codierung mit Pseudoternärcodes.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können die Ergebnisse mit dem Interaktionsmodul Signale, AKF und LDS der Pseutoternärcodes überprüfen.
Fragebogen
Musterlösung
- b1=+1_,b2=+1,b3=−1,b4=+1,b5=+1,b6=−1,
- b7=+1,b8=+1,b9=+1,b10=+1,b11=+1_,b12=−1_.
(2) Die AMI–Codierung liefert die folgenden Amplitudenkoeffizienten:
- a1=+1_,a2=0,a3=−1,a4=+1,a5=0,a6=−1,
- a7=+1,a8=0,a9=0,a10=0,a11=0_,a12=−1_.
Zu diesem Ergebnis kommt man über die Gleichung aν=(bν−bν–1)/2 oder durch direkte Anwendung der AMI–Codierregel:
- Ein Quellensymbol qν=−1 führt stets zu aν=0.
- Die Quellensymbole qν=+1 führen alternierend zu aν=+1 und aν=−1.
(3) Richtig ist der Lösungsvorschlag 1:
- Der AMI–Code liefert im Bereich zwischen ν=8 und ν=11 vier aufeinanderfolgende Nullen.
- Beim HDB3–Code würden diese vier Symbole mit „+00+” markiert. Dadurch wird zur Kenntlichmachung die AMI–Regel bewusst verletzt.
- Dagegen ersetzt der B6ZS–Code nur Nullfolgen über sechs Symbole.
(4) Unter der Annahme gleichwahrscheinlicher Binärwerte ±1 erhält man Pr(aν=0)=Pr(qν=−1)=1/2_ und aus Symmetriegründen Pr(aν=+1)=Pr(aν=−1)=1/4_.
(5) Mit den unter (4) berechneten Wahrscheinlichkeiten erhält man:
- E[aν]= 1/4⋅(+1)+1/2⋅0+1/4⋅(−1)=0_,
- E[a2ν]= 1/4⋅(+1)2+1/2⋅02+1/4⋅(−1)2=0.5_.
(6) Der AKF–Wert bei λ=0 ist gleich dem quadratischen Mittelwert der Amplitudenkoeffizienten:
- φa(λ=0)=E[a2ν]=0.5_.
Da die Ordnung des AMI–Codes N=1 ist, gilt für λ>1: φa(λ>1)=E2[aν]=0_.
Der AKF–Wert φa(λ=1) muss durch Mittelung bestimmt werden: φa(λ=1)=E[aν⋅aν+1⋅Pr(aν∩aν+1)].
Von den neun Kombinationsmöglichkeiten für aν⋅aν+1 liefern nur vier einen von0 verschiedenen Wert. In den anderen Fällen ist entweder aν=0 oder aν+1=0. Da beim AMI–Code aber auch
- Pr[(aν=+1)∩(aν+1=+1)]= 0,
- Pr[(aν=−1)∩(aν+1=−1)]= 0
zutrifft, erhält man mit
- Pr[(aν=+1)∩(aν+1=−1)]= Pr(aν=+1)⋅Pr(aν+1=−1|aν=+1)=1/4⋅1/2=1/8,
- Pr[(aν=−1)∩(aν+1=+1)]= Pr(aν=−1)⋅Pr(aν+1=+1|aν=−1)=1/4⋅1/2=1/8
als Endergebnis φa(λ=+1)=φa(λ=–1)=–0.25, da die AKF stets eine gerade Funktion ist. Hierbei ist berücksichtigt, dass nach aν=+1 mit gleicher Wahrscheinlichkeit aν+1=+1 und aν+1=−1 folgt. Damit lautet das Ergebnis:
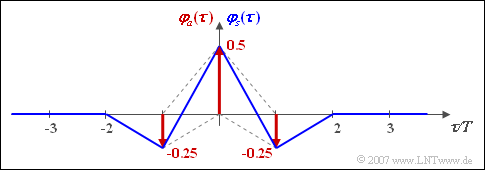
- φa(λ=0)=0.5_,
- φa(λ=1)=−0.25_,
- φa(λ=2)=0_.
Die Grafik zeigt
- die diskrete AKF φa(λ) der Amplitudenkoeffizienten und
- die AKF φs(τ) des Sendesignals unter der Voraussetzung von NRZ–Rechteckimpulsen und AMI-Codierung.
Dabei ist die blau gezeichnete AKF φs(τ) das Ergebnis der (diskreten) Faltung zwischen der diskreten AKF φa(λ) – rot gezeichnet – und der dreieckförmigen Energie–AKF des Sendegrundimpulses.
(7) Aus der angegebenen Gleichung erhält man unter Berücksichtigung der in (6) berechneten diskreten AKF-Werte φa(λ=0)=1/2,φa(|λ|=1)=–1/4 und \varphi_{a}(|\lambda| > 1) = 0$:
- Φa(f)= +∞∑λ=−∞φa(λ)⋅e−j2πfλT=φa(λ=0)+2⋅φa(λ=1)⋅cos(2πfλT)= 1/2⋅[1−cos(2πfT)]=sin2(πfT).
Insbesondere gilt:
- Φa(f=0)=0_,Φa(f=1/(2T))=sin2(π/2)=1_.