Aufgabe 3.4: GMSK–Modulation
Das bei GSM eingesetzte Modulationsverfahren ist bekanntlich Gaussian Minimum Shift Keying, abgekürtzt GMSK. Dabei handelt es sich um eine Art von FSK mit kontinuierlicher Phasenanpassung (CP–FSK), bei der
- der Modulationsindex kleinstmöglich ist, um die Orthogonalitätsbedingung noch zu erfüllen (h=0.5: „Minimum Shift Keying”),
- ein Gaußtiefpass mit Impulsantwort hG(t) vor dem FSK–Modulator eingebracht ist, um noch weiter Bandbreite einzusparen.
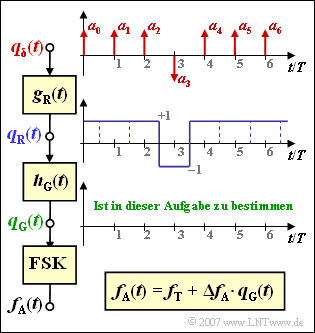
Das Bild verdeutlicht den Sachverhalt.
Die digitale Nachricht wird durch die Amplitudenkoeffizienten aν∈±1 repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete Folge für die Teilaufgabe (3) vorausgesetzt wird.
Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer TB=T:
- gR(t)={10f¨urf¨ur|t|<T/2,|t|>T/2.
Damit ergibt sich für das Rechtecksignal:
- qR(t)=qδ(t)⋆gR(t)=∑νaν⋅gR(t−ν⋅T).
Der Gaußtiefpass ist durch Frequenzgang bzw. Impulsantwort gegeben:
- HG(f)=e−π⋅(f2fG)2∙−−−∘hG(t)=2fG⋅e−π⋅(2fG⋅t)2,
wobei die systemtheoretische Grenzfrequenz fG verwendet wird. In der GSM–Spezifikation wird aber die 3dB–Grenzfrequenz mit f3dB=0.3/T angegeben. Daraus kann fG direkt berechnet werden.
Das Signal nach dem Gaußtiefpass lautet somit:
- qG(t)=qR(t)⋆hG(t)=∑νaν⋅g(t−ν⋅T).
Hierbei wird g(t) als Frequenzimpuls bezeichnet. Für diesen gilt:
- g(t)=qR(t)⋆hG(t).
Mit dem tiefpassgefilterten Signal qG(t), der Trägerfrequenz fT und dem Frequenzhub ΔfA kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden:
- fA(t)=fT+ΔfA⋅qG(t).
Verwenden Sie für Ihre Berechnungen die beispielhaften Werte fT=900 MHz und ΔfA=68 kHz.
Hinweis:
Die Aufgabe bezieht sich auf Funkschnittstelle. Verwenden Sie zur Lösung dieser Aufgabe das Gaußintegral:
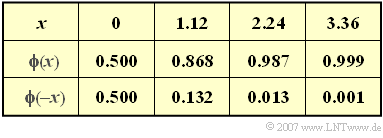
- Φ(x)=1√2π⋅∫x−∞e−u2/2du.
Insbesondere gilt:
Fragebogen
Musterlösung