Aufgabe 4.11Z: Coderate aus der Prüfmatrix

Vorgegebene Prüfmatrizen

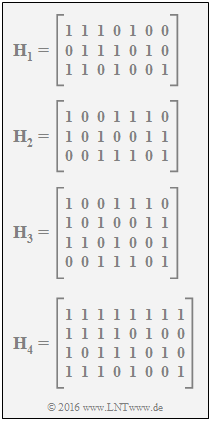
In dieser Aufgabe sollen die Coderaten der Codes $C_1, \, C_2, \, C_3$ und $C_4$ ermittelt werden, wobei die Codes allein durch ihre Prüfmatrizen gegeben sind. Eine untere Schranke für die Coderate $R$ lautet:

$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.05cm}.$

Sind die $m$ Prüfgleichungen aller Matrix–Zeilen linear unabhängig, so gilt in obiger Ungleichung das Gleichheitszeichen.

Verwendet ist hier die folgende Nomenklatur:

$w_{\rm Z}(j)$ mit $1 ≤ j ≤ m$ ist das Hamming–Gewicht der $j$ –ten Zeile der Prüfmatrix.
Durch Erwartungswertbildung ergibt sich:

${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} w_{\rm Z}(j)\hspace{0.05cm}.$

Entsprechend gibt $w_{\rm S}(i)$ mit $1 ≤ i ≤ n$ das Hamming–Gewicht der $i$ –ten Spalte von $\mathbf{H}$ an, mit dem Erwartungswert

${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} w_{\rm S}(i)\hspace{0.05cm}.$

Hinweis:

Die Aufgabe gehört um Themengebiet des Kapitels Grundlegendes zu den Low–density Parity–check Codes

Fragebogen

Musterlösung

(1) (2) (3) (4) (5)

	correct
	false