Frequenzgang und Impulsantwort

Aufruf des Applets in neuem Fenster

Applet in neuem Tab öffnen

Programmbeschreibung

noch überarbeiten

Dargestellt werden impulsförmige symmetrische Zeitsignale   ⇒   „Impulse” $x(t)$ und die dazugehörigen Spektralfunktionen $X(f)$, nämlich

• Gaußimpuls (englisch: Gaussian pulse),
• Rechteckimpuls (englisch: Rectangular pulse),
• Dreieckimpuls (englisch: Triangular pulse),
• Trapezimpuls (englisch: Trapezoidal pulse),
• Cosinus–Rolloff–Impuls (englisch: Cosine-rolloff pulse).

Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung. Die englische Beschreibung finden Sie unter Englische Version: Frequency response & Pulse response.

Weiter ist zu beachten:

• Die Funktionen $x(t)$ bzw. $X(f)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
• Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
• Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $x(t)$ (Signalwerte) bzw. $X(f)$ (Spektralwerte) sind jeweils normiert.

$\text{Beispiel:}$  Stellt man einen Rechteckimpuls mit Amplitude $A_1 = 1$ und äquivalenter Impulsdauer $\Delta t_1 = 1$ ein, so ist $x_1(t)$ im Bereich $-0.5 < t < +0.5$ gleich $1$ und außerhalb dieses Bereichs gleich $0$. Die Spektralfunktion $X_1(f)$ verläuft si–förmig mit $X_1(f= 0) = 1$ und der ersten Nullstelle bei $f=1$.

Soll mit dieser Einstellung ein Rechteckimpuls mit $A = K = 3 \ \rm V$ und $\Delta t = T = 2 \ \rm ms$ nachgebildet werden, dann sind alle Signalwerte mit $K = 3 \ \rm V$ und alle Spektralwerte mit $K \cdot T = 0.006 \ \rm V/Hz$ zu multiplizieren. Der maximale Spektralwert ist dann $X(f= 0) = 0.006 \ \rm V/Hz$ und die erste Nullstelle liegt bei $f=1/T = 0.5 \ \rm kHz$.

Theoretischer Hintergrund

Frequenzgang $H(f)$ und Impulsantwort $h(t)$

• Der Frequenzgang (oder auch die Übertragungsfunktion eines linearen zeitinvarianten Übertragungssystems $H(f)$ gibt das Verhältnis zwischen Zusammenhang zwischen Zeitfunktion $x(t)$ und dem dem Eingangsspektrum $X(f)$ an:

$$H(f) = \frac{Y(f)}{X(f)}.$$

• Ist das Übertragungsverhalten bei tiefen Frequenzen besser als bei höheren, so spricht man von einem Tiefpass (englisch: Low-pass Filter).
• Die Eigenschaften von $H(f)$ werden im Zeitbereich durch die Impulsantwort $h(t)$ ausgedrückt. Entsprechend dem zweiten Fourierintegral gilt:

$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$

• Die Gegenrichtung wird durch das erste Fourierintegral beschrieben:

$$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$

• In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt:

$$h(t)=\int_{-\infty}^{+\infty}H(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H(f)=\int_{-\infty}^{+\infty}h(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$

• Bei einem Vierpol   ⇒   $X(f)$ und $Y(f)$ haben gleiche Einheiten ist $Y(f)$ dimensionslos. Die Einheit der Impulsantwort ist $\rm 1/s$. Es gilt zwar $\rm 1/s = 1 \ Hz$, aber die Einheit „Hertz” ist in diesem Zusammenhang unüblich.
• Der Zusammenhang zwischen diesem Modul „Frequenzgang & Impulsantwort” und dem ähnlich aufgebauten Applet Impulse und Spektren basiert auf dem Vertauschungssatz.
• Alle Zeiten sind auf eine Normierungszeit $T$ normiert und alle Frequenzen auf $1/T \Rightarrow$ die Impulsantwortwerte $h(t)$ müssen noch durch die Normierungszeit $T$ dividiert werden.

$\text{Beispiel:}$  Stellt man einen Rechteck–Tiefpass mit Höhe $K_1 = 1$ und äquivalenter Bandbreite $\Delta f_1 = 1$ ein, so ist der Frequenzgang $H_1(f)$ im Bereich $-1 < f < 1$ gleich $1.5$ und außerhalb dieses Bereichs gleich $0$. Die Impulsantwort $h_1(t)$ verläuft si–förmig mit $h_1(t= 0) = 1$ und der ersten Nullstelle bei $t=1$.

Mit dieser Einstellung soll nun ein Rechteck–Tiefpass mit $\Delta f = 2 \ \rm kHz$ nachgebildet werden, wobei wir die Normierungszeit $T= 1 \ \rm ms$. Dann liegt die erste Nullstelle bei $t=0.5\ \rm ms$ und das Impulsantwortmaximum ist dann $h(t= 0) = 2 \cdot 10^3 \ \rm 1/s$.

Bitte überprüfen

Gauß–Tiefpass   $\Rightarrow$   Gaussian Low–pass

• Der Gauß–Tiefpass mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$ lautet:

$$H(f)=K\cdot {\rm e}^{-\pi\cdot(f/\Delta f)^2}.$$

• Die äquivalente Bandbreite $\Delta f$ ergibt sich aus dem flächengleichen Rechteck.
• Der Wert bei $f = \Delta f/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $f=0$.
• Für die Impulsantwort erhält man gemäß der Fourierrücktransformation:

$$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\cdot \Delta f)^2} .$$

• Je kleiner $\Delta f$ ist, um so breiter und niedriger ist die Impulsantwort   ⇒   Reziprozitätsgesetz von Bandbreite und Impulsdauer.
• Sowohl $H(f)$ als auch $h(t)$ sind zu keinem $f$- bzw. $t$-Wert exakt gleich Null.
• Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $h(t)$ bereits bei $t=1.5 \cdot \Delta t$ auf weniger als $0.1\%$ des Maximums abgefallen.

Idealer (rechteckförmiger) Tiefpass   $\Rightarrow$   Rectangular Low–pass

• Der Rechteck–Tiefpass mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$ lautet:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$

• Der $\pm \Delta f/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
• Für die Impulsantwort $h(t)$ erhält man entsprechend den Gesetzmäßigkeiten der Fourierrücktransformation (2. Fourierintegral):

$$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$

• Der $h(t)$–Wert bei $t=0$ ist gleich der Rechteckfläche des Frequenzgangs.
• Die Impulsantwort besitzt Nullstellen in äquidistanten Abständen $1/\Delta f$.
• Das Integral über die Impulsantwort $h(t)$ ist gleich dem Frequenzgang $H(f)$ bei der Frequenz $f=0$, also gleich $K$.

Dreieck–Tiefpass $\Rightarrow$ Triangular Low–pass

• Der Dreieck–Tiefpass mit der Höhe $K$ und der (äquivalenten) Bandbreite $\Delta f$ lautet:

$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$

• Die absolute physikalische Bandbreite $B$   ⇒   nur positive Frequenzen ist ebenfalls gleich $\Delta f$, also so groß wie beim Rechteck–Tiefpass.
• Für die Impulsantwort $h(t)$ erhält man gemäß der Fouriertransformation:

$$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{mit} \ {\rm si}(x)={\sin(x)}/{x}.$$

• $H(f)$ kann man als Faltung zweier Rechteckfunktionen, jeweils mit Breite $\Delta f$ darstellen.
• Daraus folgt: $h(t)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion.
• $h(t)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf.
• Der asymptotische Abfall von $X(f)$ erfolgt hier mit $1/f^2$, während zum Vergleich der Rechteckimpuls mit $1/f$ abfällt.

Trapez–Tiefpass   $\Rightarrow$   Trapezoidal Low–pass

ab hier noch anpassen Die Zeitfunktion des Trapezimpulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

• Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
• Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

• Der Sonderfall $r=0$ entspricht dem Rechteckimpuls der Sonderfall $r=1$ dem Dreieckimpuls.
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{mit} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$

• Der asymptotische Abfall von $X(f)$ liegt zwischen $1/f$ (für Rechteck, $r=0$) und $1/f^2$ (für Dreieck, $r=1$).

Cosinus-Rolloff-Tiefpass   $\Rightarrow$   Cosine-rolloff Low–pass

Die Zeitfunktion des Cosinus-Rolloff-Impulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot \frac{\pi}{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

• Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
• Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

• Der Sonderfall $r=0$ entspricht dem Rechteckimpuls der Sonderfall $r=1$ dem Cosinus-Quadrat-Impuls .
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot si(\pi \cdot \Delta t \cdot f).$$

• Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $X(f)$ asymptotisch mit $f$ ab.

Cosinus-Quadrat-Tiefpass

• Dies ist ein Sonderfall des Cosinus-Rolloff-Impulses und ergibt sich für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, t_2= \Delta t$:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\cdot \pi}{2\cdot \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$

• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$

• Wegen der letzten ${\rm si}$-Funktion ist $X(f)=0$ für alle Vielfachen von $F=1/\Delta t$. Die äquidistanten Nulldurchgänge des Cos-Rolloff-Impulses bleiben erhalten.
• Aufgrund des Klammerausdrucks weist $X(f)$ nun weitere Nulldurchgänge bei $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... auf.
• Für die Frequenz $f=\pm F/2$ erhält man die Spektralwerte $K\cdot \Delta t/2$.
• Der asymptotische Abfall von $X(f)$ verläuft in diesem Sonderfall mit $1/f^3$.

Vorschlag für die Versuchsdurchführung

„Rot” bezieht sich stets auf den ersten Parametersatz   ⇒   $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$ und „Blau” den zweiten   ⇒   $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.

(1)   Vergleichen Sie den roten Gauß–Tiefpass $(K_1 = 1, \Delta f_1 = 1)$ mit dem blauen Rechteck–Tiefpass $(K_1 = 1, \Delta f_1 = 1)$   ⇒   Voreinstellung. und beantworten Sie folgende Fragen:
(a)   Welche Signale $y(t)$ treten am Ausgang der Tiefpässe auf, wenn am Eingang das Signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $f_0 = 0.5$ anliegt? (b)   Welche Unterschiede ergeben sich $f_0 = 0.5 \pm f_\varepsilon$ mit $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$ bei beiden Tiefpässen?

(a) In beiden Fällen gilt $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ mit $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 0.912, A_2 = 1.000$. Die Phase $\varphi_0$ bleibt erhalten.

(b) Beim Gauß–Tiefpass gilt weiterhin $A_1 = 0.912$. Beim Rechteck–Tiefpass ist $A_2 = 0$ für $f_0 = 0.5000\text{...}001$ und $A_2 = 2$ für $f_0 = 0.4999\text{...}999$.

(2)   Lassen Sie die Einstellungen unverändert. Welcher Tiefpass kann das erste Nyquistkriterium oder das zweite Nyquistkriterium erfüllen, wenn $H(f)$ den Gesamtfrequenzgang von Sender, Kanal und Empfangsfilter bezeichnet.

• Um das erste Nyquistkriterium zu erfüllen, muss die Impulsantwort $h(t)$ äquidistante Nulldurchgänge bei Vielfachen der (normierten) Zeit $t = 1, 2$, ... aufweisen. Die Impulsantwort $h(t) = {\rm si}(\pi f/\Delta f)$ des Rechteck–Tiefpasses erfüllt dieses Kriterium mit $\Delta f = 1$. Dagegen ist beim Gauß–Tiefpass das erste Nyquistkriterium nie erfüllt und es kommt immer zu Impulsinterferenzen.
• Das zweite Nyquistkriterium erfüllt der Rechteck–Tiefpass dagegen nicht.

(3)   Vergleichen Sie den roten Trapez–Tiefpass $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem blauen Rechteck–Tiefpass $(K_1 = 1, \Delta f_1 = 1)$ und variieren Sie anschließend $r_1$ zwischen $0$ und $1$.

• Bei der Einstellung $r_1 = 0.5$ sind die Unterschwinger in der Impulsantwort $h(t)$ beim Trapez–Tiefpass aufgrund des flacheren Flankenabfalls geringer als beim Rechteck–Tiefpass.
• Je kleiner der Roll–off–Faktor $r_1$ wird, desto größer werden die Unterschwinger. Bei $r_1= 0$ ist der Trapez–Tiefpass identisch mit dem Rechteck–Tiefpass   ⇒   $h(t)= {\rm si}(\pi \cdot t)$.
• Erhöht man dagegen den Roll–off–Faktor $r_1$, so größer werden die Unterschwinger kleiner. Bei $r_1= 1$ ist der Trapez–Tiefpass identisch mit dem Dreieck–Tiefpass   ⇒   $h(t)= {\rm si}^2(\pi \cdot t)$.

(4)   Vergleichen Sie den roten Trapez–Tiefpass $(K_1 = 1, \Delta f_1 = 1, r_1 = 0.5)$ mit dem blauen Cosinus-Rolloff-Tiefpass $(K_2 = 1,\Delta f_2 = 1.0, r_1 = 0.5)$ und und variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_2(f)$ für $r_2 = 0.7$.

Fragen und Antworten noch überarbeiten

• Der Vergleich von Trapezimpuls $x_1(t)$ und Cosinus-Rolloff-Impuls $x_2(t)$ bei gleichem Rolloff-Faktor $r= 0.5$ zeigt, dass $X_2(f)$ für $f > 1$ größere betragsmäßige Anteile besitzt als ist $X_1(f)$.
• Bei gleichem Rolloff-Faktor $r_1 = r_2= 0.5$ verläuft der Flankenabfall des Cosinus-Rolloff-Impulses $x_2(t)$ um die Frequenz $f = 0.5$ steiler als der Flankenabfall des Trapezimpulses $x_2(t)$. Mit $r_1 = 0.5$ und $r_2 = 0.7$ gilt $x_1(t) \approx x_2(t)$ und damit auch $X_1(f) \approx X_2(f)$.

(5)   Vergleichen Sie den roten Trapez–Tiefpass' $(K_1 = 1, \Delta f_1 = 1, r_1 = 1)$ mit dem blauen Cosinus-Rolloff-Impuls $(K_2 = 1,\Delta f_2 = 1.0, r_1 = 1)$. Interpretieren Sie die Funktionen $x_1(t)$ und $X_1(f)$.

Fragen und Antworten noch überarbeiten

• Es handelt sich bei $x_1(t) = \cos^2(|t| \cdot \pi/2) \ \ \text{für} \ |t| \le 1$ um den Cosinus-Quadrat-Impuls.
• Wegen $\Delta t = 1$ besitzt $X_1(f)$ Nulldurchgänge bei $\pm 1$, $\pm 2$, ...
• Weitere Nulldurchgänge gibt es bei $f=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... , nicht jedoch bei $\pm 0.5$.
• Für die Frequenz $f=\pm 0.5$ erhält man die Spektralwerte $0.5$.
• Der asymptotische Abfall von $X_1(f)$ verläuft in diesem Sonderfall mit $1/f^3$.

Zur Handhabung des Programms

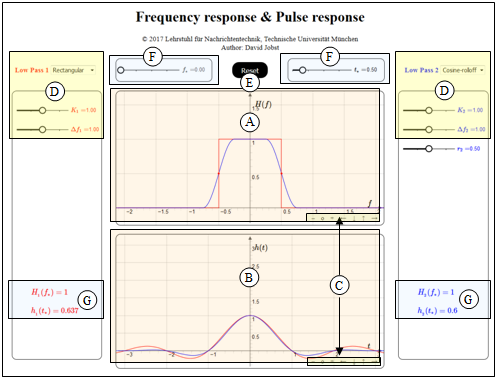
    (A)     Bereich der graphischen Darstellung für $H(f)$

    (B)     Bereich der graphischen Darstellung für $h(t)$

    (C)     Variationsmöglichkeit für die graphischen Darstellungen

    (D)     Parametereingabe per Slider
                      links (rot): „Low–pass 1”,         rechts (blau): „Low–pass 2”

    (E)     Parameter entsprechend der Voreinstellung   ⇒   „Reset”

    (F)     Einstellung von $t_*$ und $f_*$ für Numerikausgabe

    (G)     Numerikausgabe von $H(f_*)$ und $h(t_*)$
                      links (rot): „Low–pass 1”,         rechts (blau): „Low–pass 2”

Details zum obigen Punkt (C)

    (*)   Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)

    (*)   Verschiebe–Funktionen „$\leftarrow$” (Bildausschnitt nach links, Ordinate nach rechts) sowie „$\uparrow$” „$\downarrow$” „$\rightarrow$”

Andere Möglichkeiten:

• Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
• Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
• 2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen