Aufgabe 5.7: OFDM–Sender mittels IDFT

• Zurück zum Buch

Blockschaltbild der Inversen Diskreten Fouriertransformation (IDFT)

In dieser Aufgabe wird ein OFDM–Sender genauer betrachtet, der mit Hilfe der Inversen Diskreten Fouriertransformation (IDFT) realisiert wird. Dabei gelte:

• Das System habe $N = 4$ Träger.
• Die Rahmendauer sei $T_{\ \rm R} = 0.25 \ \rm ms$.
• Ein Guard–Intervall wird nicht verwendet.
• In einem Rahmen werden $16$ Bit übertragen.

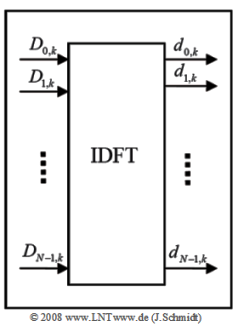
Die Grafik rechts oben zeigt den Block „IDFT„ der OFDM–Senderstruktur. Jeweils vier Bit ergeben hierbei ein komplexes Symbol gemäß der unten gegebenen 16–QAM–Signalraumzuordung.

Hinweise:

• Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
• Bezug genommen wird auch auf das Kapitel Diskrete Fouriertransformation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Die Gleichung der IDFT lautet mit $ν = 0$, ... , $N–1$:

$$d_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu ,k} \cdot w^{ - \nu \cdot \mu } } \quad {\rm{mit}} \quad w = {\rm{e}}^{ - {\rm{j}} {\rm{2\pi}}/N}.$$

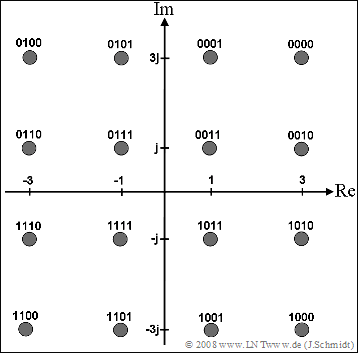
Für die 16–QAM soll in dieser Aufgabe von folgender Signalraumkonstellation ausgegangen werden:

Vorgeschlagene 16–QAM-Signalraumzuordnung

Fragebogen

1

Geben Sie die maximale Datenbitrate des Systems an.

$R_{\rm B} \ = \ $ $\ \rm kbit/s$

2

Geben Sie für die gegebene 16–QAM–Signalraumzuordnung die komplexen Trägerkoeffizienten $D_\mu$ für die folgenden Eingangsbitfolgen an.

${\rm Re}[D_0] \ = \ $ $\ \ \text{für die Bitfolge 1111}$

${\rm Im}[D_0] \ = \ $

${\rm Re}[D_1] \ = \ $ $\ \ \text{für die Bitfolge 0111}$

${\rm Im}[D_1] \ = \ $

${\rm Re}[D_2] \ = \ $ $\ \ \text{für die Bitfolge 1000}$

${\rm Im}[D_2] \ = \ $

${\rm Re}[D_3] \ = \ $ $\ \ \text{für die Bitfolge 0000}$

${\rm Im}[D_3] \ = \ $

3

Berechnen Sie daraus die diskreten Zeitbereichswerte $d_\nu$ innerhalb des Rahmens.

${\rm Re}[d_0] \ = \ $

${\rm Im}[d_0] \ = \ $

${\rm Re}[d_1] \ = \ $

${\rm Im}[d_1] \ = \ $

${\rm Re}[d_2] \ = \ $

${\rm Im}[d_2] \ = \ $

${\rm Re}[d_3] \ = \ $

${\rm Im}[d_2] \ = \ $

4

Welche Aussagen sind für den Crest–Faktor zutreffend, der das Verhältnis von Spitzenwert zu Effektivwert einer Wechselgröße bezeichnet?

	Der Crest–Faktor ist bei einem OFDM–System eher gering.
	Der Crest–Faktor kann bei OFDM–Systemen sehr groß werden.
	Ein großer Crest–Faktor kann zu Realisierungsproblemen führen.

Musterlösung

Musterlösung

1. Da hier kein Guard–Intervall berücksichtigt wird, ist die Symboldauer T gleich der Rahmendauer $T_R = 0.25 ms$. Bei N = 4 Trägern und 16–QAM gilt für die Bitrate am Eingang: $$R_{\rm{B}} = \frac{1}{T_{\rm{B}}} = \frac{4 \cdot {\rm{log}_2}\hspace{0.08cm}(16)}{T} = \frac{4 \cdot 4}{0.25\,\,{\rm ms}}\hspace{0.15cm}\underline {= 64\,\,{\rm kbit/s}}.$$

2. Aus der Signalraumzuordnung folgt für die Trägerkoeffizienten (auf den Index k wird verzichtet):

$${\rm{Bitfolge}}\hspace{0.5cm}1111:\hspace{1cm} D_0 = -1 - {\rm{j}},$$ $${\rm{Bitfolge}}\hspace{0.5cm}0111:\hspace{1cm} D_1 = -1 + {\rm{j}},$$ $${\rm{Bitfolge}}\hspace{0.5cm}1000:\hspace{1cm} D_2 = +3 - 3{\rm{j}},$$ $${\rm{Bitfolge}}\hspace{0.5cm}0000:\hspace{1cm} D_3 = +3 + 3{\rm{j}}.$$

3. Die angegebene IDFT–Gleichung lautet mit N = 4:

$$d_{\nu } = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu } \cdot {\rm{e}}^{ \hspace{0.04cm} {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} \pi/2 \hspace{0.04cm}\cdot \hspace{0.04cm}\nu \hspace{0.04cm}\cdot \hspace{0.04cm} \mu } } .$$ Daraus erhält man für ν = 0, ... , 3: $$d_0 = D_0 + D_1 +D_2 +D_3 = 4,$$ $$d_1 = D_0 + {\rm{j}} \cdot D_1 - D_2 -{\rm{j}} \cdot D_3 = -2 + 2 \cdot {\rm{j}},$$ $$d_2 = D_0 - D_1 + D_2 - D_3 = -8 \cdot {\rm{j}},$$ $$d_3 = D_0 - {\rm{j}} \cdot D_1 - D_2 +{\rm{j}} \cdot D_3 = -6 + 6 \cdot {\rm{j}}.$$

4. Richtig sind die beiden letzten Lösungsvorschläge. Bei OFDM ist der Crest–Faktor eher groß, was bei den verwendeten Verstärkerschaltungen zu Problemen in Bezug auf Linearitätsanforderungen und Energieeffizienz führen kann.