Aufgabe 4.13: FSK–Demodulation

• Zurück zum Buch

Signalverläufe der FSK–Demodulation

Im Theorieteil wurde bereits das Blockschaltbild des kohärenten FSK–Demodulators angegeben, wobei wir in dieser Aufgabe von der unteren Systemvariante ausgehen. Rauschanteile werden hier nicht betrachtet.

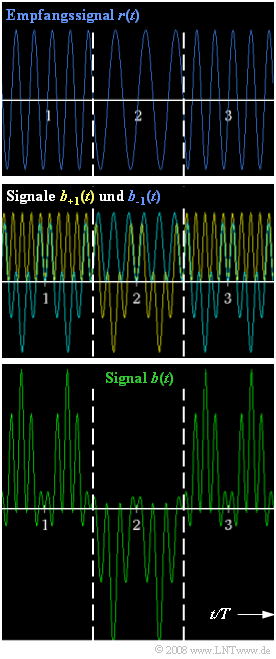
Die rechts angegebene Grafik zeigt die Signalverläufe an verschiedenen Stellen des Blockschaltbildes, wobei jeweils drei Symbole gezeichnet sind, im Bild getrennt durch gestrichelte Linien:

• Oben ist das Empfangssignal $r(t)$ dargestellt, das identisch mit dem FSK–Sendesignal ist. Die höhere Frequenz $f_{+1}$ gehört zum Amplitudenkoeffizienten $a_ν = +1$, während $a_ν = –1$ mit der Frequenz $f_{–1}$ dargestellt ist. Bezogen auf die Symbolmitten $T$, $2T$, $3T$, ... liegt jeweils ein sinusförmiger Verlauf vor. Der konstante Betrag der Hüllkurve ist $s_0$.
• Das mittlere Diagramm zeigt die Signale nach der Multiplikation mit den jeweiligen Sinussignalen:

$$b_{\rm +1}(t) = r(t) \cdot 2 \cdot \sin (2 \pi \cdot f_{\rm +1} \cdot t )\hspace{0.05cm},$$

$$b_{\rm -1}(t) = r(t) \cdot 2 \cdot \sin (2 \pi \cdot f_{\rm -1} \cdot t ) \hspace{0.05cm}.$$

Das Signal $b_{+1}(t)$ im oberen Demodulatorzweig ist gelb und das Signal $b_{–1}(t)$ im unteren Zweig blau dargestellt. Der grüne Verlauf gilt entsprechend der Farbenlehre für beide Kurven. Die Signale sind gegenüber $r(t)$ niedriger als dargestellt.

• Der untere Signalverlauf zeigt das Differenzsignal $b(t) = b_{+1}(t) – b_{–1}(t)$. Das folgende Matched–Filter kann auch als Integrator realisiert werden. Damit ist der (normierte) Entscheidungswert für das $ν$–te Symbol wie folgt gegeben:

$$E_{\nu}= \frac{1}{s_0} \cdot d (\nu \cdot T + T/2) = \frac{1}{s_0 \cdot T} \cdot \int_{(\nu - 1/2) T }^{(\nu + 1/2) T }\hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
• Bezug genommen wird insbesondere auf die Seite Kohärente Demodulation der FSK.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben ist die trigonometrische Beziehung

$$2 \cdot \sin(\alpha) \cdot \sin(\beta)= \cos(\alpha - \beta)- \cos(\alpha + \beta) \hspace{0.05cm}.$$

Fragebogen

1

Wie lauten die Amplitudenkoeffizienten:

$a_1$ =

$a_2$ =

$a_3$ =

2

Geben Sie die beiden Frequenzen $f_{+1}$ und $f_{–1}$ an.

$f_{+1}$ = $\cdot 1/T$

$f_{–1}$ = $\cdot 1/T$

3

Welche Aussagen treffen für das Signal $b_{+1}(t)$ im ersten Zeitintervall zu?

	Das Signal beinhaltet die Frequenz 2/T.
	Das Signal beinhaltet die Frequenz 4/T.
	Das Signal beinhaltet die Frequenz 6/T.
	Das Signal beinhaltet die Frequenz 8/T.
	Das Signal beinhaltet die Frequenz 10/T.
	Das Signal beinhaltet einen Gleichanteil.

4

Welche Aussagen treffen für das Signal $b_{–1}(t)$ im ersten Zeitintervall zu?

	Das Signal beinhaltet die Frequenz 2/T.
	Das Signal beinhaltet die Frequenz 4/T.
	Das Signal beinhaltet die Frequenz 6/T.
	Das Signal beinhaltet die Frequenz 8/T.
	Das Signal beinhaltet die Frequenz 10/T.
	Das Signal beinhaltet einen Gleichanteil.

5

Welche normierten Entscheidungswerte ergeben sich für die einzelnen Symbole?

$E_1$ =

$E_2$ =

$E_3$ =

Musterlösung

Musterlösung

1. Im mittleren Bereich ist eine niedrigere Frequenz als in den beiden äußeren Bereichen zu erkennen: $$a_1 \hspace{0.15cm}\underline {= +1},\hspace{0.2cm}a_2 \hspace{0.15cm}\underline {= -1},\hspace{0.2cm}a_3\hspace{0.15cm}\underline { = +1} \hspace{0.05cm}.$$

2. Aus der Grafik erkennt man im ersten und im letzten Zeitintervall fünf Schwingungen und im zweiten Intervall drei Schwingungen: $$f_{\rm +1} \hspace{0.15cm}\underline {= 5 \cdot 1/T},\hspace{0.2cm}f_{\rm -1}\hspace{0.15cm}\underline { = 3 \cdot 1/T} \hspace{0.05cm}.$$ Die Trägerfrequenz ist somit $f_T = 4/T$ und der Frequenzhub $Δf_A = 1/T$.

3. In diesem Bereich gilt, wobei der erste Term das Empfangssignal r(t) beschreibt: $$b_{\rm +1}(t) = s_0 \cdot \sin (2 \pi \cdot 5/T \cdot t )\cdot 2 \cdot \sin (2 \pi \cdot 5/T \cdot t )=$$ $$= s_0 \cdot \left [ 1 - \cos (2 \pi \cdot 10/T \cdot t )\right ] \hspace{0.05cm}.$$ Richtig sind demnach die beiden letzten Lösungsvorschläge.

4. Für das untere Signal $b_{–1}(t)$ gilt im gleichen Zeitintervall: $$b_{\rm -1}(t) = s_0 \cdot \sin (2 \pi \cdot 5/T \cdot t )\cdot 2 \cdot \sin (2 \pi \cdot 3/T \cdot t )=$$ $$= s_0 \cdot \left [ \cos (2 \pi \cdot 2/T \cdot t ) - \cos (2 \pi \cdot 8/T \cdot t )\right ] \hspace{0.05cm}$$ Richtig sind somit die Lösungsvorschläge 1 und 4.

5. Für den ersten Entscheidungswert gilt mit $b(t) = b_{+1}(t) – b_{–1}(t)$: $$E_{1} = \frac{1}{s_0 \cdot T} \cdot \int_{T/2 }^{3T/2} b_{\rm +1} (t )\hspace{0.1cm} {\rm d}t - \frac{1}{s_0 \cdot T} \cdot \int_{T/2 }^{3T/2} b_{\rm -1} (t )\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$ Aus dem Ergebnis der Teilaufgabe d) erkennt man, dass das zweite Integral 0 ergibt (Integration über Vielfache der Periodendauer von Sinusfunktionen). Das erste Integral ist gleich $s_0 · T$. Daraus folgt für den Entscheidungswert im ersten Zeitintervall: $E_1 = +1$. Ebenso ist $E_3 = +1$. Dagegen ist bei der Berechnung von $E_2$ das erste Integral 0 und das zweite hat den Wert $s_0 · T$. Somit erhält man hierfür den Wert $E_2 = –1$.