Aufgabe 3.15: Data Processing Theorem

• Zurück zum Buch

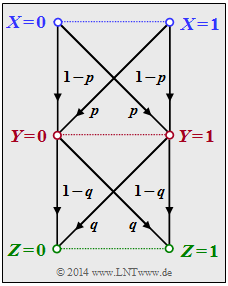
Wir betrachten die folgende Datenverarbeitungskette:

• Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ verarbeitet, der durch bedingte Wahrscheinlichkeiten $(P_Y|X)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$.
• Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z|Y}$gegeben. $Z$ hängt allein von $Y$ ab (entweder deterministisch oder stochastisch) und ist unabhängig von $X$:

$$P_{Z\hspace{0.01cm}|\hspace{0.01cm} XY\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} x, y) =P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Hierbei wurde folgende Nomenklatur benutzt: $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ Die Verbund–Wahrscheinlichkeitsfunktion (englisch: Joint Probability Mass Function) lautet: $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.01cm}|\hspace{0.01cm} X\hspace{-0.03cm}}(y\hspace{0.01cm}|\hspace{0.01cm} x)\cdot P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Das bedeutet auch: $X → Y → Z$ bilden eine Markovkette. Für eine solche gilt das Data Processing Theorem mit folgender Konsequenz: $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},\\ I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$ Das Theorem besagt somit:

• Man kann durch Manipulation (Processing) der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
• Datenverarbeitung (durch den Prozessor 2) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.

Hinweis: Die Aufgabe gehört zu Kapitel 3.3.

Fragebogen

1

Wie lässt sich das Ergebnis $I(X; Y) = 1 – H_{bin}(p)$ herleiten?

	Über die Eigenschaften eines streng symmetrischen Kanals.
	Weil $H_{bin}(p)$ eine konkave Funktion ist.
	Das Ergebnis gilt für jede Wahrscheinlichkeitsfunktion $P_X(X).$

2

Welche Transinformation ergibt sich für den Prozessor $1$ mit $p = 0.1$?

$p = 0.1: I(X; Y)$ = $bit$

3

Welche Transinformation ergibt sich für den Prozessor 2 mit $q = 0.2$?

$q = 0.2: I(Y; Z)$ = $bit$

4

Welche Transinformation ergibt sich für das Gesamtsystem?

$p = 0.1, q = 0.2: I(X; Z)$ = $bit$

5

Erfüllt dieses Beispiel das Data Processing Theorem?

	ja
	nein

Musterlösung

Musterlösung

1. Beide Prozessoren beschreiben streng symmetrische Kanäle $⇒$ sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend. Für einen solchen Binärkanal gilt mit $Y = \{0, 1\} ⇒ |Y| = 2:$ $$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{\hspace{0.01cm}Y \mid \hspace{0.01cm} X}(y|x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \mid \hspace{0.01cm} X}(y|x) \hspace{0.05cm}.$$ Hierbei ist es völlig egal, ob man von $X = 0$ oder von $X = 1$ ausgeht. Für $X = 0$ erhält man mit $P_{Y|X}(Y = 1|X = 0) = p$ und $P_{Y|X}(Y = 0|X = 0) = 1 – p:$ $$I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm},$$ $${\rm mit}\hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ Das Ergebnis gilt allerdings nur für $P_X(X) = [0.5, 0.5] ⇒$ maximale Transinformation $⇒$ Kanalkapazität. Andernfalls ist $I(X; Y)$ kleiner. Beispielsweise gilt für $PX_(X) = [1, 0]$: $H(X) = 0 ⇒ I(X; Y) = 0.$

Richtig ist also nur der Lösungsvorschlag 1. Die binäre Entropiefunktion ist zwar konkav, aber diese Eigenschaft wurde bei der Herleitung nicht benutzt.

2. Für den Prozessor $1$ ergibt sich mit $p = 0.1:$ $$I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$

3. Entsprechend gilt für den zweiten Prozessor mit $q = 0.2$: $$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$

4. Die Wahrscheinlichkeit für $Z = 0$ unter der Bedingung $X = 0$ ergibt sich über zwei Wege zu $$P(\hspace{0.01cm}Z\hspace{-0.05cm} = \hspace{-0.05cm}0 \mid \hspace{0.01cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$ Das Gesamtsystem hat dann die genau gleiche BSC–Struktur wie die Prozessoren $1$ und $2$, aber nun mit der Verfälschungswahrscheinlichkeit $$\varepsilon = p + q - 2pq \hspace{0.05cm}.$$ Für $p = 0.1$ und $q = 0.2$ erhält man $$\varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26$$ $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$

5. Die Antwort ist natürlich JA, da beim Data Processing Theorem genau von den hier gegebenen Voraussetzungen ausgegangen wird. Wir wollen aber zusätzlich einige numerische Ergebnisse auswerten:

• Gilt $0 ≤ p < 0.5$ und $0 ≤ q < 0.5$, so erhält man:

$$varepsilon \hspace{-0.15cm} =\hspace{-0.15cm} p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$ $$\varepsilon \hspace{-0.15cm} = \hspace{-0.15cm} q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$

• Für $p = 0.5$ gilt unabhängig von $q$, da $I(X; Z)$ nicht größer sein kann als $I(X; Y)$:

$$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ Ebenso erhält man mit $q = 0.5$ unabhängig von $p$: $$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ Auch für $p < 0.5$ und $q > 0.5$ wird das Data Processing Theorem nicht verletzt, was hier nur an einem Beispiel gezeigt werden soll. Mit $p = 0.1$ und $q = 0.8$ erhält man das gleiche Ergebnis wie in Teilaufgabe (d): $$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74$$ $$\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$