Beispiele binärer Blockcodes

1. Kanalcodierung
2. Binäre Blockcodes zur Kanalcodierung
3. Beispiele binärer Blockcodes

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Single Parity–check Codes

Der  Single Parity–check Code  $\rm (SPC)$  fügt zu dem Informationsblock  $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$  ein Prüfbit  (englisch:  "Parity")  $p$  hinzu:

Verschiedene  "Single Parity–check Codes"  $(n = k + 1)$

$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$

$$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$

Die Grafik zeigt drei Coder–Beispiele mit

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \ (k = 3)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \ (k = 4)$.

Dieser sehr einfache Code kann wie folgt charakterisiert werden:

• Aus  $n = k + 1$  folgt für die  Coderate  $R = k/n = (n-1)/n$  und für die  Redundanz  $1-R = 1/n$.  Für  $k = 2$  ergibt sich zum Beispiel die Coderate  $2/3$  und die relative Redundanz beträgt  $33.3\%$.

• Das Prüfbit erhält man durch die  Modulo–2–Addition.  Darunter versteht man die Addition im  Galoisfeld  zur Basis  $2$   ⇒   $\rm GF(2)$,  sodass  $1 \oplus 1 = 0$  ergibt:

$$p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.$$

• Damit enthält jedes gültige Codewort  $\underline{x}$  eine gerade Anzahl von Einsen.  Ausgedrückt mit  $\oplus$  bzw. in vereinfachter Schreibweise gemäß der zweiten Gleichung lautet diese Bedingung:

$$x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm oder:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}.$$

• Für  $k = 2$   ⇒   $n = 3$  ergeben sich die folgenden vier Codeworte,  wobei das Prüfbit  $p$  jeweils durch einen kleinen Pfeil markiert ist:

$$\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.$$

• Dieser Code  $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$  ist  linear,  da die Summe zweier beliebiger Codeworte wieder ein gültiges Codewort ergibt,  zum Beispiel

$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$

• Für beliebiges  $k$   ⇒   $n = k+1$  unterscheidet sich jedes Codewort von allen anderen an einer geraden Anzahl von Positionen.  Die minimale Distanz des Codes ist also 

$$d_{\rm min} = 2.$$

$\text{Definition:}$  Jeder  $\text{Single Parity–check Code (SPC)}$  lässt sich formal wie folgt beschreiben:

$$\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm mit \hspace{0.15cm}geradzahliger\hspace{0.15cm} Anzahl\hspace{0.15cm} von\hspace{0.15cm} Einsen\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.$$

• Mit der allgemeinen Codebezeichnung  $(n, \ k, \ d_{\rm min})$  lässt sich jeder  "Single Parity–check Code"  auch mit  $\text{SPC }(n, \ n-1, \ 2)$  benennen.
• Die obere Grafik zeigt somit den  $\text{SPC (3, 2, 2)}$,  den  $\text{SPC (4, 3, 2)}$  und den  $\text{SPC (5, 4, 2)}$.

Der digitale Kanal ändert möglicherweise das Codewort  $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$  in das Empfangswort  $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. Mit dem Fehlervektor  $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$  gilt:

$$\underline{y}= \underline{x} \oplus \underline{e}.$$

Zur Decodierung des Single Parity–check Codes bildet man das so genannte  Syndrom:

$$s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.$$

Das Ergebnis  $s=1$  weist dann auf  (mindestens)  einen Bitfehler innerhalb des Codewortes hin,  während  $s=0$  wie folgt zu interpretieren ist:

• Die Übertragung war fehlerfrei,  oder:
  
• Die Anzahl der Bitfehler ist geradzahlig.
  
  

$\text{Beispiel 1:}$  Wir betrachten den  $\text{SPC (4, 3, 2)}$  und gehen davon aus,  dass das Nullwort gesendet wurde.  Die Tabelle zeigt alle Möglichkeiten,  dass  $f$  Bit verfälscht werden und gibt das jeweilige Syndrom  $s \in \{0, 1\}$  an.

Mögliche Empfangswerte beim  $\text{SPC (4, 3, 2)}$

Für das  BSC–Modell  mit der Verfälschungswahrscheinlichkeit  $\varepsilon = 1\%$  ergeben sich dann folgende Wahrscheinlichkeiten:

• Das Informationswort wird richtig decodiert  (blaue Hinterlegung):

$${\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.$$

• Der Decoder erkennt, dass Übertragungsfehler aufgetreten sind  (grüne Hinterlegung):

$${\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f}$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr}(s=1) \hspace{-0.1cm} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.$$

• Das Informationswort wird falsch decodiert  (rote Hinterlegung):

$${\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.$$

Wir verweisen hier auf das HTML5/JavaScript–Applet  "Binomial- und Poissonverteilung".  Die hier gewonnenen Ergebnisse werden auch in  Aufgabe 1.5  diskutiert.

$\text{Beispiel 2:}$  Eine Fehlerkorrektur des Single Parity–check Codes ist beim BSC–Modell nicht möglich im Unterschied zum  BEC–Modell. 

Bei diesem werden Bitfehler ausgeschlossen.  Ist nur ein Bit ausgelöscht  $($englisch:   "Erasure",  $\rm E)$,  so ist aufgrund der Tatsache  „die Anzahl der Einsen im Codewort ist gerade”  auch eine Fehlerkorrektur möglich,  zum Beispiel für den  $\text{SPC (5, 4, 2)}$:

$$\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},$$ $$\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},$$ $$\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.$$

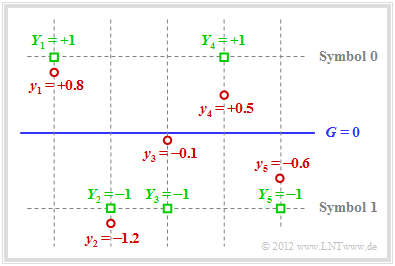
$\text{Beispiel 3:}$  Auch beim  AWGN–Kanal  ist Fehlerkorrektur möglich,  wenn man  "Soft Decision"  anwendet.  Für das Folgende gehen wir von bipolarer Signalisierung aus:

Zur Verdeutlichung von „Soft Decision” bei AWGN

• $x=0$   ⇒   $\tilde{x}= +1$,  sowie
• $x=1$   ⇒   $\tilde{x}= -1$.
  

Die Grafik verdeutlicht den hier dargelegten Sachverhalt:

• Beispielsweise lautet der Empfangsvektor  (rote Punkte):

$$\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.$$

• Bei harter Entscheidung  (Schwelle  $G = 0$,  nur die Vorzeichen werden ausgewertet)  würde man zu folgendem binären Ergebnis kommen  $($grüne Quadrate  $Y_i = y_i/ \vert y_i \vert)$:

$$\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.$$

• In Symbolschreibweise ergibt sich  $(0, 1, 1, 0, 1)$,  was kein gültiges  $\text{SPC (5, 4, 2)}$–Codewort ist   ⇒   Syndrom  $s = 1$.  Also müssen ein, drei oder fünf Bit verfälscht worden sein.
  

• Die Wahrscheinlichkeit für drei oder fünf Bitfehler ist allerdings um Größenordnungen kleiner als diejenige für einen einzigen Fehler.  Die Annahme  „ein Bitfehler”  ist deshalb nicht abwegig.
  

• Da der Empfangswert  $y_3$  sehr nahe an der Schwelle  $G = 0$  liegt,  geht man davon aus,  dass genau dieses Bit verfälscht wurde.  Damit fällt bei  "Soft Decision"  die Entscheidung für  $\underline{z} = (0, 1, 0, 0, 1)$   ⇒   $\underline{v} = (0, 1, 0, 0)$.  Die Blockfehlerwahrscheinlichkeit  ${\rm Pr}(\underline{v} \ne \underline{u})$  ist so am geringsten.

Wiederholungscodes

$\text{Definition:}$  Ein  $\text{Wiederholungscode}$  (englisch:   "Repetition Code", $\rm RC)$  ist ein linearer binärer  $(n, \, k)$–Blockcode der Form

$$\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.15cm}{\rm f\ddot{u}r \hspace{0.15cm}alle\hspace{0.25cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.$$

• Der Codeparameter  $n$  bezeichnet die Codelänge. Unabhängig von  $n$  gilt stets  $k = 1$.

• Entsprechend existieren nur die zwei Codeworte  $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$  und  $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$,  die sich in  $n$  Binärstellen unterscheiden.

• Daraus folgt für die minimale Distanz  $d_{\rm min} = n$.

Verschiedene Wiederholungscodes ("Repetition Codes")

Die Grafik zeigt Wiederholungscodes für  $n=3$,  $n=4$  und  $n=5$.  Ein solcher Wiederholungscode weist folgende Eigenschaften auf:

• Dieser  $(n, \, 1, \, n)$–Blockcode besitzt die sehr kleine Coderate  $R = 1/n$,  ist also nur für die Übertragung bzw. Speicherung kleiner Dateien geeignet.

• Andererseits ist der Wiederholungscode sehr robust.

• Beim  BEC–Kanal  ("Binary Erasure Channel")  genügt ein richtig übertragenes Bit an beliebiger Position  (alle anderen Bit können ausgelöscht sein),  um das Informationswort richtig zu decodieren.
  

$\text{Beispiel 4: Decodierung und Fehlerwahrscheinlichkeiten beim BSC–Kanal}$

Es gelte das  BSC–Modell  mit  $\varepsilon = 10\%$.  Die Decodierung basiere auf dem Majoritätsprinzip.

• Bei ungeradem  $n$  können  $e=n-1$  Bitfehler erkannt und  $t=(n-1)/2$  Bitfehler korrigiert werden.  Damit ergibt sich für die Wahrscheinlichkeit der korrekten Decodierung der Informationsbits  $u$:

$${\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.$$

• Die nachfolgenden Zahlenwerte gelten für  $n = 5$.  Das heißt:   Es sind  $t = 2$  Bitfehler korrigierbar:

$${\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%$$

$$\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.$$

• Bei geradem  $n$  können dagegen nur  $t=n/2-1$  Fehler korrigiert werden.  Erhöht man  $n$  von  $5$  auf  $6$, so sind weiterhin auch nur zwei Bitfehler innerhalb eines Codewortes korrigierbar. Einen dritten Bitfehler kann man zwar nicht korrigieren, aber zumindest erkennen:

$${\rm Pr}({\rm nicht\hspace{0.15cm} korrigierbarer\hspace{0.15cm} Fehler}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}.$$

• Ein  (unerkannter)  Decodierfehler  $(v \ne u)$  ergibt sich erst,  wenn innerhalb des 6 Bit–Wortes vier oder mehr Bit verfälscht wurden.  Als Näherung unter der Annahme,  dass fünf oder sechs Bitfehler sehr viel unwahrscheinlicher sind als vier,  gilt:

$${\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.$$

• Interessant ist, dass beim  $\text{RC(6, 1, 6)}$  die Wahrscheinlichkeit  ${\rm Pr}(v = u)$  für eine mögliche und richtige Decodierung mit  $98.42\%$  kleiner ist als beim  $\text{RC (5, 1, 5)}$. Für letzteren gilt:  ${\rm Pr}(v = u) = 1 \approx 99.15\%.$

$\text{Beispiel 5: Leistungsfähigkeit des Wiederholungscodes beim AWGN–Kanal}$

Wir betrachten nun den  AWGN–Kanal.  Bei uncodierter Übertragung  $($oder dem Wiederholungscode mit  $n=1)$   ist der Empfangswert  $y = \tilde{x}+\eta$,  wobei  $\tilde{x} \in \{+1, -1\}$ das Informationsbit bei bipolarer Signalisierung bezeichnet und  $\eta$  den Rauschterm.  Um Verwechslungen mit dem Codeparameter  $n$  zu vermeiden, haben wir das Rauschen umbenannt:   $n → \eta$.

Für die Fehlerwahrscheinlichkeit gilt mit dem  komplementären Gaußschen Fehlerintegral  ${\rm Q}(x)$

$${\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},$$

wobei folgende physikalische Größen zu verwenden sind:

• Das Signal–zu–Rauschleistungsverhältnis  $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,
  

• die Energie  $E_{\rm S}$  pro Codesymbol   ⇒   „Symbolenergie”,
  

• die normierte Streuung  $\sigma$  des Rauschens, gültig für das bipolare Informationsbit  $\tilde{x} \in \{+1, -1\}$,  und
  

• die konstante (einseitige) Rauschleistungsdichte  $N_0$  des AWGN–Rauschens.
  
  

Fehlerwahrscheinlichkeit des Wiederholungscodes beim AWGN–Kanal

Bei einem  $(n,\ 1,\ n)$–Wiederholungscode ergibt sich dagegen für den Eingangswert des Maximum–Likelihood–Decoders  $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$  mit folgenden Eigenschaften:

$$\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Amplitude}$$

$$\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fache \hspace{0.15cm}Leistung}\hspace{0.05cm},$$

$$\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Varianz:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},$$

$$\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.$$

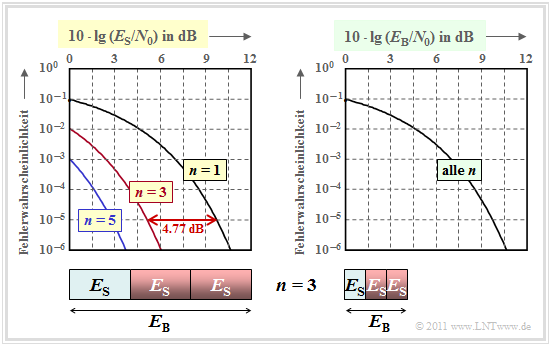
Die Fehlerwahrscheinlichkeit in doppelt logarithmischer Darstellung zeigt die linke Grafik.

1. Als Abszisse ist  $10 \cdot \lg \, (E_{\rm S}/N_0)$  aufgetragen.
2. Die Energie pro Bit  $(E_{\rm B})$  ist  $n$  mal größer als die Symbolenergie  $(E_{\rm S})$,  wie im Schaubild für  $n=3$  verdeutlicht.

Diese Kurvenschar kann wie folgt interpretiert werden:

• Trägt man die Fehlerwahrscheinlichkeit über der Abszisse  $10 \cdot \lg \, (E_{\rm S}/N_0)$  auf,  so ergibt sich durch  $n$–fache Wiederholung gegenüber uncodierter Übertragung  $(n=1)$  eine signifikante Verbesserung.
  

• Die Kurve für den Wiederholungsfaktor  $n$  erhält man durch Linksverschiebung um  $10 \cdot \lg \, n$  (in dB)  gegenüber der Vergleichskurve.  Der Gewinn beträgt  $4.77 \ {\rm dB} \ (n = 3)$ bzw. $\approx 5 \ {\rm dB} \ (n = 5)$.
  

• Allerdings ist ein Vergleich bei konstantem  $E_{\rm S}$  nicht fair,  da man mit dem  $\text{RC (5, 1, 5)}$  für die Übertragung eines Informationsbits eine um den Faktor  $n$  größere Energie aufwendet als bei uncodierter Übertragung:   $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$

Aus der rechten Grafik erkennt man,  dass alle Kurven genau übereinander liegen,  wenn auf der Abszisse  $10 \cdot \lg \, (E_{\rm B}/N_0)$  aufgetragen wird.

$\text{Fazit bezüglich Wiederholungscodes beim AWGN–Kanal:}$

• Die Fehlerwahrscheinlichkeit ist bei fairem Vergleich unabhängig vom Wiederholungsfaktor  $n$:     ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$

• Beim AWGN–Kanal ist durch einen Wiederholungscode kein  Codiergewinn  zu erzielen.

Hamming–Codes

Richard Wesley Hamming  hat 1962 eine Klasse binärer Blockcodes angegeben,  die sich durch die Anzahl  $m = 2, 3, \text{...}$  der zugesetzten  "Parity Bits"  unterscheiden.  Für diese Codeklasse gilt:

• Die Codelänge ergibt sich stets zu  $n = 2^m -1$.  Möglich sind demzufolge beim Hamming–Code auch nur die Längen  $n = 3$,  $n = 7$,  $n = 15$,  $n = 31$,  $n = 63$,  $n = 127$,  $n = 255$, usw.
  

• Ein Informationswort besteht aus  $k = n-m$  Bit.  Die Coderate ist somit gleich

$$R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.$$

• Alle Hamming–Codes haben die minimale Distanz  $d_{\rm min} = 3.$  Bei größerer Codelänge  $n$  erreicht man  $d_{\rm min} = 3$  schon mit weniger Redundanz,  also bei größerer Coderate  $R$.  Aus  $d_{\rm min} = 3$  folgt weiter, dass hier  $e = d_{\rm min} -1 =2$  Fehler erkannt werden können und man  $t = (d_{\rm min} -1)/2 = 1$  Fehler korrigieren kann.
  

• Der Hamming–Code  $\text{HC (3, 1, 3)}$  ist identisch mit dem Wiederholungscode  $\text{RP (3, 1, 3)}$  und lautet:  $\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \big \}\hspace{0.05cm}.$

• Bei systematischer Codierung sind die ersten  $k$  Stellen eines jeden Hamming–Codewortes  $\underline{x}$  identisch mit dem Informationswort  $\underline{u}$.  Anschließend folgen dann die  $m = n-k$  Paritätsbit:

$$\underline{x} = ( x_1,\ x_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ x_n) = ( u_1,\ u_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k,\ p_1,\ p_2, \hspace{0.05cm}\text{...} \hspace{0.05cm},\ p_{n-k}) \hspace{0.05cm}.$$

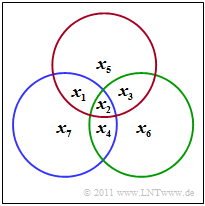
$\text{Beispiel 6: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$

Der  $\text{(7, 4, 3)}$–Hamming–Code wird durch das dargestellte Schaubild verdeutlicht. Daraus kann man die drei Bedingungen ableiten:

Verdeutlichung des $\text{(7, 4, 3)}$–Hamming–Codes

$$x_1 \oplus x_2 \oplus x_3 \oplus x_5 = 0 \hspace{0.05cm},$$

$$x_2 \oplus x_3 \oplus x_4 \oplus x_6 = 0 \hspace{0.05cm},$$

$$x_1 \oplus x_2 \oplus x_4 \oplus x_7 = 0 \hspace{0.05cm}.$$

• Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung,  der grüne die zweite und der blaue die letzte.

• In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.

Zuordnung $\underline{u} → \underline{x}$ des systematischen $\text{(7, 4, 3)}$–Hamming–Codes

Bei systematischer Codierung des  $\text{(7, 4, 3)}$–Hamming–Codes

$$x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3$$

lauten die Bestimmungsgleichungen der drei Prüfbit, wie aus dem Schaubild hervorgeht:

$$p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},$$

$$p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},$$

$$p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.$$

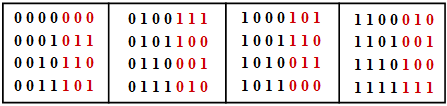
Die Tabelle zeigt die  $2^k = 16$  zulässigen Codeworte des systematischen  $\text{(7, 4, 3)}$–Codes:

$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3).$$

• Das Informationswort  $\underline{u} =( u_1, u_2, u_3, u_4)$  ist schwarz dargestellt und die Prüfbits  $p_1$,  $p_2$  und  $p_3$  rot.

• Man erkennt anhand dieser Tabelle, dass sich jeweils zwei der  $16$  möglichen Codeworte in mindestens  $d_{\rm min} = 3$  Binärwerten unterscheiden.

Später wird die  Decodierung linearer Blockcodes  noch ausführlich behandelt.  Das folgende Beispiel soll die Decodierung des Hamming–Codes eher intuitiv erklären.

$\text{Beispiel 7: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$

Wir gehen weiter vom systematischen  $\text{(7, 4, 3)}$–Code aus und betrachten das Empfangswort  $\underline{y} = ( y_1,\ y_2,\ y_3,\ y_4,\ y_5,\ y_6,\ y_7)$.

Zur Decodierung bilden wir die drei Paritätsgleichungen

$$y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)}$$

$$y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)}$$

$$y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}$$

Im Folgenden bezeichnet  $\underline{v}$  das Decodierergebnis;  dieses sollte stets mit  $\underline{u} = (1, 0, 1, 0)$  übereinstimmen:

Unter der Voraussetzung,  dass in jedem Codewort höchstens ein Bit verfälscht wird,  gelten dann die folgenden Aussagen. 

• Das Empfangswort  $\underline{y} = (1, 0, 1, 0, 0, 1, 1)$  erfüllt alle drei Paritätsgleichungen.  Das heißt,  dass kein einziger Übertragungsfehler aufgetreten ist   ⇒   $\underline{y} = \underline{x}$   ⇒   $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Werden zwei der drei Paritätsgleichungen erfüllt wie zum Beispiel für das empfangene Wort  $\underline{y} =(1, 0, 1, 0, 0, 1, 0)$,  so wurde ein Paritätsbit verfälscht und es gilt auch hier  $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Mit  $\underline{y} = (1, 0, 1, 1, 0, 1, 1)$  wird nur die Gleichung  $\rm (I)$  erfüllt und die beiden anderen nicht.  Somit kann man die Verfälschung des vierten Binärsymbols korrigieren,  und es gilt auch hier  $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Ein Übertragungsfehler des zweiten Bits   ⇒   $\underline{y} = (1, 1, 1, 0, 0, 1, 1)$  führt dazu,  dass alle drei Paritätsgleichungen nicht erfüllt werden.  Auch dieser Fehler lässt sich eindeutig korrigieren,  da nur  $u_2$  in allen Gleichungen vorkommt.

Aufgaben zum Kapitel

Aufgabe 1.5: SPC (5, 4) und BEC–Modell

Aufgabe 1.5Z: SPC (5, 4) vs. RC (5, 1)

Aufgabe 1.6: Zum (7, 4)–Hamming–Code