Aufgabe 4.13Z: AMI-Code

• Zurück zum Buch

AKF bei AMI-Codierung

Zur Spektralanpassung  (Formung)  eines Digitalsignals an die Eigenschaften des Kanals verwendet man so genannte  "Pseudoternärcodes".  Bei diesen Codes wird die binäre Quellensymbolfolge  $\langle q_\nu \rangle$  nach einer festen Vorschrift in eine Folge  $\langle c_\nu \rangle$  von Ternärsymbolen umgesetzt:

$$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$

Der bekannteste Vertreter dieser Codeklasse ist der AMI-Code  (von  "Alternate Mark Inversion").  Hier wird

• der Binärwert  $q_\nu = -1$  stets auf  $c_\nu = 0$  abgebildet,
• während  $q_\nu = +1$  abwechselnd  (alternierend)  durch die Ternärwerte  $c_\nu = +1$  und  $c_\nu = -1$  dargestellt wird.

Vereinbarungsgemäß soll beim ersten Auftreten von  $q_\nu = +1$  das Ternärsymbol  $c_\nu = +1$  ausgewählt werden.

Weiter wird vorausgesetzt,  dass

• die zwei möglichen Quellensymbole jeweils gleichwahrscheinlich sind,  und
• die Quellensymbolfolge  $\langle q_\nu \rangle$  keine inneren statistischen Bindungen aufweist.

Somit sind alle diskreten AKF-Werte gleich Null mit Ausnahme von  $\varphi_q(k=0)$:

$$\varphi_q ( k \cdot T) = 0, \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$

Hierbei bezeichnet  $T$  den zeitlichen Abstand der Quellensymbole.  Verwenden Sie den Wert  $T = 1 \hspace{0.05cm} \rm µ s$.  Die Codesymbole haben den gleichen Abstand.

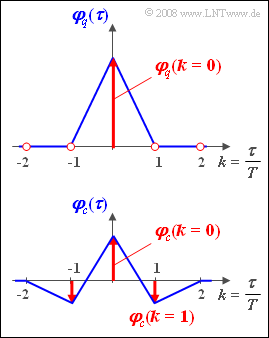
Das Bild zeigt die gegebenen Autokorrelationsfunktionen.  Bitte beachten Sie:

• Rot eingezeichnet sind jeweils die zeitdiskreten Darstellungen  ${\rm A} \{ \varphi_q(\tau) \}$  und  ${\rm A} \{ \varphi_c(\tau) \}$  der Autokorrelationsfunktionen,  jeweils mit dem Bezugswert  $T$.
• Die blau dargestellten Funktionen zeigen die zeitkontinuierlichen Verläufe  $\varphi_q(\tau)$  und  $\varphi_c(\tau)$  der AKF,  wobei Rechteckimpulse vorausgesetzt sind.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Leistungsdichtespektrum.
• Bezug genommen wird auch auf das Kapitel  Autokorrelationsfunktion  sowie auf die Seite  Numerische LDS-Ermittlung.
• Benutzen Sie folgende Fourierkorrespondenz;  ${\rm \Delta} (t)$  bezeichnet einen um  $t = 0$  symmetrischen Dreieckimpuls mit  ${\rm \Delta} (t= 0) = 1$  und  ${\rm \Delta} (t) = 0$  für  $|t| \ge T$:

$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$

Fragebogen

1

Wie groß ist der diskrete AKF–Wert der Quellensymbole für  $k = 0$?

$\varphi_q(k=0) \ = \ $

2

Welche Aussagen gelten für die LDS–Funktionen  ${\it \Phi}_q(f)$  und  ${\rm P} \{ {\it \Phi}_q(f) \}$?

	${\rm P} \{ {\it \Phi}_q(f) \}$  ist für alle Frequenzen eine Konstante.
	${\it \Phi}_q(f)$  ist für  $|f \cdot T| < 0.5$  konstant und außerhalb Null.
	${\it \Phi}_q(f)$  verläuft  $\rm si^2$-förmig.

3

Die Quellensymbolfolge sei  $\langle q_\nu \rangle = \langle +1, -1, +1, +1, -1, +1, +1, -1, -1, -1 \rangle$.
Wie lauten die Codesymbole  $c_\nu$ ? Geben Sie das Codesymbol  $c_6$  ein.

$c_6 \ = \ $

4

Wie groß ist der diskrete AKF–Wert der Codesymbole für  $k = 0$.

$\varphi_c(k=0) \ = \ $

5

Berechnen Sie die AKF-Werte  $\varphi_c(k=+1)$  und  $\varphi_c(k=-1)$.

$\varphi_c(k=+1) \ = \ $

$\varphi_c(k=-1) \ = \ $

6

Welche spektrale Leistungsdichte  ${\it \Phi}_c(f)$  ergibt sich für die Frequenz $f=0$ bzw. für $f = 500 \hspace{0.08cm} \rm kHz$.   Hinweis:   Für  $|k| \ge 2$  sind alle AKF–Werte  $\varphi_c(k) \equiv 0$.

${\it \Phi}_c(f = 0) \ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

${\it \Phi}_c(f = 500 \hspace{0.08cm} \rm kHz)\ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

Musterlösung

Musterlösung

(1)  Der diskrete AKF-Wert für  $k = 0$  gibt die Varianz der Quellensymbole an.

• Da  $q_\nu$  nur die Werte  $-1$  und  $+1$  annehmen kann,  ist  $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$.

(2)  Richtig sind  die Lösungsvorschläge 1 und 3:

• Die zeitdiskrete AKF und deren Fouriertransformierte lauten:

$${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$

• Es ist berücksichtigt, dass  $\varphi_q(k=0)= \sigma_q^2= 1$  ist.  Das bedeutet:  Die periodische Fortsetzung von  ${\rm P} \{ {\it \Phi}_q(f) \}$  ergibt für alle Frequenzen den gleichen Wert.
• Dagegen kann die zeitkontinuierliche AKF wie folgt dargestellt werden:  

$$\varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \Delta} ( \tau) / T ).$$

• Das dazugehörige Leistungsdichtespektrum  (Fouriertransformierte der AKF)  ist dann das Produkt der Fouriertransformierten der beiden Faltungsterme:  

$${\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$$

• Aufgrund der gewählten AKF-Interpolation (mit Geradenabschnitten) aus ihren Abtastwerten ergibt sich ein  $\rm si^2$-förmiges Leistungsdichtespektrum.
• Ein rechteckförmiges Spektrum gemäß Lösungsvorschlag  (2)  würde sich nur bei  $\rm si$-förmiger Interpolation einstellen.

(3)  Die codierte Folge lautet:   $\langle +1, \ 0, -1, +1, \ 0, -1, +1, \ 0, \ 0, \ 0 \rangle$.  Das 6. Symbol ist somit  $c_6\hspace{0.15cm}\underline{= -1}$.

(4)  Die Auftrittswahrscheinlichkeiten der Werte  $-1$ , $\ 0$  und $+1$  sind  $0.25,  0.5,  0.25$.  Daraus folgt:

$$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}.$$

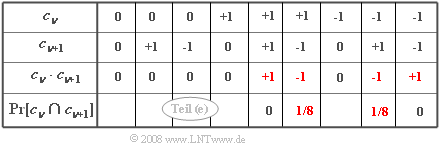
(5)  Für den AKF-Wert bei  $k = 1$  betrachtet man das Produkt  $c_{\nu} \cdot c_{\nu+1}$.  Es ergeben sich die in der Tabelle gezeigten Kombinationen.

• Einen Beitrag liefern nur Produkte  $c_{\nu} \cdot c_{\nu+1} \ne 0$  mit  ${\rm Pr}\big[c_{\nu} \cdot c_{\nu+1}\big] \ne 0$:

$$\varphi_c ( k = 1) = {\rm Pr} \big [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] \cdot (+1) \cdot (-1) + {\rm Pr} \big [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \big ] \cdot (-1) \cdot (+1).$$

Zur AKF-Berechnung des AMI-Codes

• In der Tabelle sind diese Terme rot gekennzeichnet. Weiter gilt:

$${\rm Pr} \big [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] =$$

$$= {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} .$$

• Hierbei ist vorausgesetzt, dass  $+1$  mit der Wahrscheinlichkeit  $0.25$  auftritt und danach  $-1$  nur in der Hälfte der Fälle folgt.
• Das gleiche Ergebnis erhält man für den zweiten Beitrag. Damit gilt:

$$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$

$$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$

• Zur Berechnung von  $\varphi_c ( k = 2)$  muss über  $3^3 = 27$  Kombinationen gemittelt werden. Das Ergebnis ist Null.

(6)  Die Fouriertransformierte der zeitdiskreten AKF  ${\rm A} \{ \varphi_c(\tau) \}$  lautet:

$${\rm P} \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$

• Mit dem Ergebnis der letzten Teilaufgabe folgt daraus:

$${\rm P} \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$

• Wie unter Punkt  (2) gezeigt,  gilt dann für das LDS  –  also die Fouriertransformierte von  $\varphi_c(\tau)$:

$${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$

$$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$