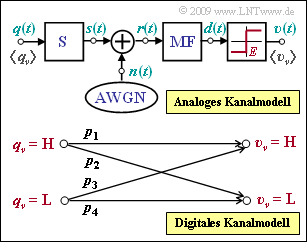
Die Grafik zeigt oben das analoge Kanalmodell eines digitalen Übertragungssystems, wobei das additive Rauschsignal $n(t)$ mit der (zweiseitigen) Rauschleistungsdichte $N_0/2$ wirksam ist. Es handelt sich um AWGN–Rauschen. Die Varianz des Rauschanteils vor dem Entscheider (nach dem Matched–Filter) ist dann
- $$\sigma^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$
Weiter soll gelten:
- Es treten keine Impulsinterferenzen auf. Wurde das Symbol $q_{\nu} = \mathbf{H}$ gesendet, so ist der Nutzanteil des Detektionssignal gleich $+s_0$, bei $q_{\nu} = \mathbf{L}$ dagegen $-s_0$.
- Der Schwellenwertentscheider berücksichtigt eine Schwellendrift, das heißt, die Schwelle $E$ kann durchaus vom Optimalwert $E = 0$ abweichen. Die Entscheidungsregel lautet:
- $$\upsilon_\nu = \left\{ \begin{array}{c} \mathbf{H} \\ \mathbf{L} \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}d (\nu \cdot T) > E \hspace{0.05cm}, \\ {\rm falls} \hspace{0.15cm} d (\nu \cdot T) \le E\hspace{0.05cm}.\\ \end{array}$$
- Mit dem Schwellenwert $E = 0$ ergibt sich die mittlere Fehlerwahrscheinlichkeit zu
- $$p_{\rm M} = {\rm Q} \left ( {s_0}/{\sigma} \right ) = 0.01\hspace{0.05cm}.$$
Die untere Grafik zeigt ein digitales Kanalmodell, das durch die vier Übergangswahrscheinlichkeiten $p_1, p_2, p_3$ und $p_4$ charakterisiert ist. Dieses soll an das analoge Kanalmodell angepasst werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Binary Symmetric Channel (BSC).
- Zahlenwerte der Q–Funktion können mit dem interaktiven Applet Komplementäre Gaußsche Fehlerfunktionen ermittelt werden.
Fragebogen
Musterlösung
- Daraus folgt für den Quotienten aus Detektionsnutzabtastwert und Detektionsstöreffektivwert:
- $${s_0}/{\sigma}= {\rm Q}^{-1} \left ( 0.01 \right ) \hspace{0.15cm}\underline {\approx 2.32}\hspace{0.05cm}.$$
(2) Mit $E = 0$ ergibt sich für die Wahrscheinlichkeiten des vorgegebenen digitalen Kanalmodells:
- $$p_2 = p_3 = p = 0.01 \hspace{0.05cm}, \hspace{0.2cm}p_1 = p_4 = 1-p = 0.99\hspace{0.05cm}.$$
- Ein Vergleich mit dem Theorieteil zeigt, dass dieses Kanalmodell dem BSC–Modell entspricht, und zwar unabhängig von der Statistik der Quellensymbole.
- Richtig sind also beide Lösungsvorschläge.
(3) Die Übergangswahrscheinlichkeit $p_2$ beschreibt nun den Fall, dass die Enscheiderschwelle $E = 0.25 \cdot s_0$ fälschlicherweise unterschritten wurde.
- Dann ist $v_{\nu} = \mathbf{L}$, obwohl $q_{\nu} = \mathbf{H}$ gesendet wurde. Der Abstand von der Schwelle beträgt somit nur $0.75 \cdot s_0$ und es gilt:
- $$p_{\rm 2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Q} \left ( \frac{0.75 \cdot s_0}{\sigma} \right ) = {\rm Q} \left ( 0.75 \cdot 2.32 \right ) = {\rm Q} \left ( 1.74 \right )\hspace{0.15cm}\underline {\approx 0.041}\hspace{0.05cm}, \hspace{0.5cm} p_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}1 - p_{\rm 2} \hspace{0.15cm}\underline {= 0.959}\hspace{0.05cm}.$$
- In ähnlicher Weise können die Übergangswahrscheinlichkeiten $p_3$ und $p_4$ berechnet werden, wobei nun vom Schwellenabstand $1.25 \cdot s_0$ auszugehen ist:
- $$p_{\rm 3} = {\rm Q} \left ( 1.25 \cdot 2.32 \right ) = {\rm Q} \left ( 2.90 \right )\hspace{0.15cm}\underline {\approx 0.002}\hspace{0.05cm}, \hspace{0.2cm} p_{\rm 4} = 1 - p_{\rm 3}\hspace{0.15cm}\underline { = 0.998}\hspace{0.05cm}.$$
(4) Keiner der beiden Lösungsvorschläge trifft zu:
- Mit der Entscheiderschwelle $E ≠ 0$ ist das BSC–Modell unabhängig von der Symbolstatistik nicht anwendbar,
- da die Symmetrieeigenschaft des Kanals (das Kennzeichen „S” in „BSC”) nicht gegeben ist.
(5) Die Aussagen 1 und 3 treffen zu, nicht aber die Aussage 2:
- Beim BSC–Modell ist $p_{\rm M} = 1\%$ unabhängig von den Symbolwahrscheinlichkeiten $p_{\rm L}$ und $p_{\rm H}$.
- Dagegen gilt für $p_{\rm L} = 0.9$, $p_{\rm H} = 0.1$ sowie $E = +s_0/4$:
- $$p_{\rm M} = 0.9 \cdot p_{\rm 3} + 0.1 \cdot p_{\rm 2}= 0.9 \cdot 0.2\% + 0.1 \cdot 4.1\% \approx 0.59\% \hspace{0.05cm}.$$
- Das Minimum ergibt sich für $p_{\rm L} = 0.93$ und $p_{\rm H} = 0.07$ zu $p_{\rm M} \approx 0.45\%$.
