Wir gehen vom[ AWGN-Kanalmodell aus:
- $X$ kennzeichnet den Eingang (Sender).
- $N$ steht für eine gaußverteilte Störung.
- $Y = X +N$ beschreibt den Ausgang (Empfänger) bei additiver Störung.
Für die Wahrscheinlichkeitsdichtefunktion der Störung gelte:
- $$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$
Da die Zufallsgröße $N$ mittelwertfrei ist ⇒ $m_{N} = 0$, kann man die Varianz $\sigma_{\hspace{-0.05cm}N}^2$ mit der Leistung $P_N$ gleichsetzen. In diesem Fall ist die differentielle Entropie der Zufallsgröße $N$ wie folgt angebbar (mit der Pseudo–Einheit „bit”):
- $$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$
In dieser Aufgabe wird $P_N = 1\hspace{0.1cm} \rm mW$ vorgegeben. Dabei ist zu beachten:
- Die Leistung $P_N$ in obiger Gleichung muss wie die Varianz $\sigma_{\hspace{-0.05cm}N}^2$ dimensionslos sein.
- Um mit dieser Gleichung arbeiten zu können, muss die physikalische Größe $P_N$ geeignet normiert werden, zum Beispiel entsprechend $P_N = 1\hspace{0.1cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$.
- Bei anderer Normierung, beispielsweise $P_N = 1\hspace{0.1cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 0.001$ ergäbe sich für $h(N)$ ein völlig anderer Zahlenwert.
Weiter können Sie für die Lösung dieser Aufgabe berücksichtigen:
- Die Kanalkapazität ist definiert als die maximale Transinformation zwischen Eingang $X$ und Ausgang $Y$ bei bestmöglicher Eingangsverteilung:
- $$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) \hspace{0.05cm}.$$
- Die Kanalkapazität des AWGN–Kanals lautet:
- $$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$
- Man erkennt: Die Kanalkapazität $C$ und auch die Transinformation $I(X; Y)$ sind im Gegensatz zu den differentiellen Entropien unabhängig von obiger Normierung.
- Bei gaußförmiger Stör–WDF $f_N(n)$ führt eine ebenfalls gaußförmige Eingangs–WDF $f_X(x)$ zur maximalen Transinformation und damit zur Kanalkapazität.
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
- Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log2” verwendet.
Fragebogen
Musterlösung
- $$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$
- Mit $C_{\rm bit} = 2$ ergibt sich daraus:
- $$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N \hspace{0.15cm}\underline{= 15\,{\rm mW}} \hspace{0.05cm}. $$
(2) Richtig sind die Lösungsvorschläge 1 bis 4. Begründung:
- Für $P_X < 15 \ \rm mW$ wird die Transinformation $I(X; Y)$ stets kleiner als $2$ bit sein, unabhängig von allen anderen Gegebenheiten.
- Mit $P_X = 15 \ \rm mW$ ist die maximale Transinformation $I(X; Y) = 2$ bit nur erreichbar, wenn die Eingangsgröße $X$ gaußverteilt ist.
Die Ausgangsgröße $Y$ ist dann ebenfalls gaußverteilt. - Weist die Zufallsgröße $X$ einen Gleichanteil $m_X$ auf, so ist die Varianz $\sigma_X^2 = P_X - m_X^2 $ bei gegebenem $P_X$ kleiner, und es gilt $I(X; Y) = 1/2 · \log_2 \ (1 + \sigma_X^2/P_N) < 2$ bit.
- Voraussetzung für die gegebene Kanalkapazitätsgleichung ist, dass $X$ und $N$ unkorreliert sind.
- Wären dagegen die Zufallsgrößen $X$ und $N$ unkorreliert, so ergäbe sich $I(X; Y) = 0$.
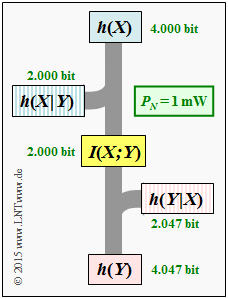
(3) Die angegebene Gleichung für die differentielle Entropie macht nur bei dimensionsloser Leistung Sinn. Mit der vorgeschlagenen Normierung erhält man:
- Für $P_N = 1 \ \rm mW$ ⇒ $P_N\hspace{0.05cm}' = 1$:
- $$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$
- Für $P_X = 15 \ \rm mW$ ⇒ $P_X\hspace{0.01cm}' = 15$:
- $$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \right ) + {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) \hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}. $$
- Für $P_Y = P_X + P_N = 16 \ \rm mW$ ⇒ $P_Y\hspace{0.01cm}' = 16$:
- $$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} \hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$
(4) Für die differentielle Irrelevanz gilt beim AWGN–Kanal:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$
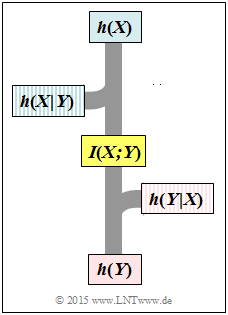
- Entsprechend nebenstehender Grafik gilt aber auch:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$
- Daraus kann die differentielle Äquivokation wie folgt berechnet werden:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$
- Abschließend wird auch noch die differentielle Verbundentropie angegeben, die aus obigem Schaubild nicht direkt ablesbar ist:
- $$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$
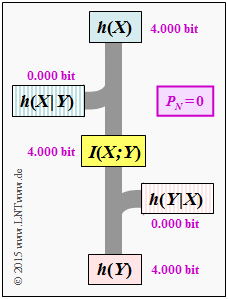
(5) Beim idealen Kanal erhält man mit $h(X)\hspace{0.15cm}\underline{= 4.000 \,{\rm bit}}$:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$
- $$h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$
- $$I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$
- Die Grafik zeigt diese Größen in einem Flussdiagramm.
- Das gleiche Diagramm ergäbe sich auch im wertdiskreten Fall mit $M = 16$ gleichwahrscheinlichen Symbolen ⇒ $H(X)= 4.000 \,{\rm bit}$.
- Man müsste nur jedes $h$ durch ein $H$ ersetzen.