Aufgabe 3.7: Einige Entropieberechnungen
Wir betrachten die beiden Zufallsgrößen XY und UV mit den folgenden 2D-Wahrscheinlichkeitsfunktionen:
- PXY(X,Y)=(0.180.160.020.64)
- PUV(U,V)=(0.0680.1320.2720.528)
Für die Zufallsgröße XY sollen in dieser Aufgabe berechnet werden:
- die Verbundentropie (englisch: "Joint Entropy"):
- H(XY)=−E[log2PXY(X,Y)],
- die beiden Einzelentropien:
- H(X)=−E[log2PX(X)],
- H(Y)=−E[log2PY(Y)].
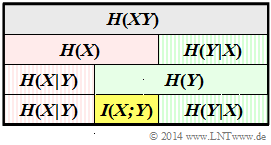
Daraus lassen sich gemäß dem obigen Schema – dargestellt für die Zufallsgröße XY – auch folgende Beschreibungsgrößen sehr einfach bestimmen:
- die bedingten Entropien (englisch: "Conditional Entropies"):
- H(X|Y)=−E[log2PX|Y(X|Y)],
- H(Y|X)=−E[log2PY|X(Y|X)],
- die Transinformation (englisch: "Mutual Information") zwischen X und Y:
- I(X;Y)=E[log2PXY(X,Y)PX(X)⋅PY(Y)].
Abschließend sind qualitative Aussagen hinsichtlich der zweiten Zufallsgröße UV zu verifizieren.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seiten
Bedingte Wahrscheinlichkeit und bedingte Entropie sowie
Transinformation zwischen zwei Zufallsgrößen.
Fragebogen
Musterlösung
(1) Aus der gegebenen Verbundwahrscheinlichkeit erhält man
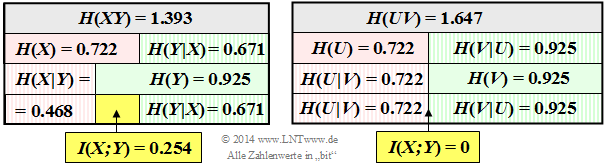
- H(XY)=0.18⋅log210.18+0.16⋅log210.16+0.02⋅log210.02+0.64⋅log210.64=1.393(bit)_.
(2) Die 1D–Wahrscheinlichkeitsfunktionen lauten PX(X)=[0.2, 0.8] und PY(Y)=[0.34, 0.66]. Daraus folgt:
- H(X)=0.2⋅log210.2+0.8⋅log210.8=0.722(bit)_,
- H(Y)=0.34⋅log210.34+0.66⋅log210.66=0.925(bit)_.
(3) Aus der Grafik auf der Angabenseite erkennt man den Zusammenhang:
- I(X;Y)=H(X)+H(Y)−H(XY)=0.722(bit)+0.925(bit)−1.393(bit)=0.254(bit)_.
(4) Ebenso gilt entsprechend der Grafik auf der Angabenseite:
- H(X∣Y)=H(XY)−H(Y)=1.393−0.925=0.468(bit)_,
- H(Y∣X)=H(XY)−H(X)=1.393−0.722=0.671(bit)_
- Die linke Grafik fasst die Ergebnisse der Teilaufgaben (1), ... , (4) maßstabsgetreu zusammen.
- Grau hinterlegt ist die Verbundentropie und gelb die Transinformation.
- Eine rote Hinterlegung bezieht sich auf die Zufallsgröße X, eine grüne auf Y. Schraffierte Felder deuten auf eine bedingte Entropie hin.
Die rechte Grafik beschreibt den gleichen Sachverhalt für die Zufallsgröße UV ⇒ Teilaufgabe (5).
(5) Richtig sind gemäß dem Schaubild die Aussagen 1, 2 und 4:
- Man erkennt die Gültigkeit von PUV=PU·PV ⇒ Transinformation I(U;V)=0 daran,
dass die zweite Zeile der PUV–Matrix sich von der ersten Zeile nur durch einen konstanten Faktor (4) unterscheidet. - Es ergeben sich gleiche 1D–Wahrscheinlichkeitsfunktionen wie für die Zufallsgröße XY ⇒ PU(U)=[0.2, 0.8] und PV(V)=[0.34, 0.66].
- Deshalb ist auch H(U)=H(X)=0.722 bit und H(V)=H(Y)=0.925 bit.
- Hier gilt aber nun für die Verbundentropie: H(UV)=H(U)+H(V)≠H(XY).