Aufgabe 3.6Z: Optimaler Nyquistentzerrer für Exponentialimpuls

• Zurück zum Buch

Beidseitig abfallender Exponentialimpuls

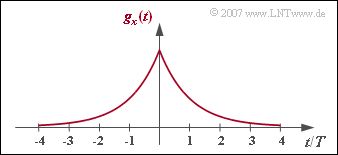
Wie in der  Aufgabe 3.6  betrachten wir wieder den optimalen Nyquistentzerrer, wobei nun als Eingangsimpuls  $g_x(t)$  eine beidseitig abfallende Exponentialfunktion anliegt:

$$g_x(t) = {\rm e }^{ - |t|/T}\hspace{0.05cm}.$$

• Durch ein Transversalfilter  $N$–ter Ordnung mit der Impulsantwort

$$h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T)$$

ist es immer möglich, dass der Ausgangsimpuls  $g_y(t)$  Nulldurchgänge bei  $t/T = ±1, \ \text{...} \ , \ t/T = ±N$  aufweist und  $g_y(t = 0) = 1$  ist.

• Im allgemeinen Fall führen dann allerdings die Vorläufer und Nachläufer mit  $| \nu | > N$  zu Impulsinterferenzen.

Hinweis:  Die Aufgabe gehört zum Kapitel  "Linare Nyquistentzerrung".

Fragebogen

1

Geben Sie die Signalwerte  $g_x(\nu) = g_x(t = \nu T)$  bei Vielfachen von  $T$  an.

$g_x(0)\ = \ $

$g_x(1)\ = \ $

$g_x(2)\ = \ $

2

Berechnen Sie die optimalen Filterkoeffizienten für  $N = 1$.

$k_0 \ = \ $

$k_1 \ = \ $

3

Berechnen Sie die Ausgangswerte  $g_2 = g_{y}(t = 2T)$  und  $g_3 = g_{y}(t = 3T)$.

$g_2 \ = \ $

$g_3\ = \ $

4

Welche der folgenden Aussagen sind zutreffend?

	Beim gegebenen Eingangsimpuls  $g_x(t)$  ist mit einem Transversalfilter zweiter Ordnung keine Verbesserung möglich.
	Die erste Aussage ist unabhängig vom Eingangsimpuls  $g_x(t)$.
	Beim gegebenen Eingangsimpuls ergibt sich mit einem „unendlichen” Transversalfilter eine weitere Verbesserung.

Musterlösung

Musterlösung

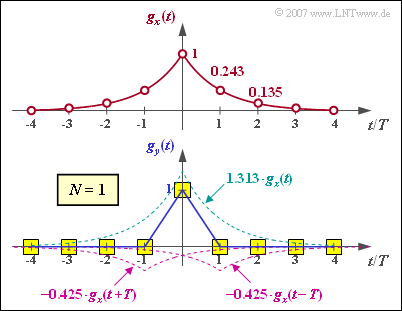
(1)  Die fünf ersten Abtastwerte des Eingangsimpulses im Abstand  $T$  lauten:

$$g_x(0)\hspace{0.25cm}\underline{ = 1},\hspace{0.2cm}g_x(1) \hspace{0.25cm}\underline{= 0.368},\hspace{0.25cm}g_x(2) \hspace{0.25cm}\underline{= 0.135},\hspace{0.2cm}g_x(3) = 0.050,\hspace{0.2cm}g_x(4) {= 0.018} \hspace{0.05cm}.$$

(2)  Entsprechend der  Aufgabe 3.6  kommt man auf folgendes Gleichungssystem:

$$2t = T \hspace{-0.1cm}:\hspace{0.2cm}g_1 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} k_0 \cdot g_x(1) +k_1 \cdot [g_x(0)+g_x(2)]= 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{k_1}{k_0} = - \frac{g_x(1)}{g_x(0)+g_x(2)} \hspace{0.05cm},$$

$$t = 0 \hspace{-0.1cm}:\hspace{0.2cm}g_0 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} k_0 \cdot g_x(0) + k_1 \cdot 2 \cdot g_x(1) = 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_1 = \frac{1-k_0}{0.736} \hspace{0.05cm}.$$

• Dies führt zum Ergebnis:

$$k_0 - 0.324 \cdot 0.736 \cdot k_0 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_0 \hspace{0.15cm}\underline {= 1.313}, \hspace{0.2cm}k_1\hspace{0.15cm}\underline { = -0.425} \hspace{0.05cm}.$$

Eingangsimpuls  (oben),  und Ausgangsimpuls für  $N = 1$

(3)  Für den Zeitpunkt  $t = 2T$  gilt:

$$g_2 \ = \ k_0 \cdot g_x(2) +k_1 \cdot [g_x(1)+g_x(3)]$$

$$\Rightarrow\hspace{0.3cm} g_2 \ = \ 1.313 \cdot 0.050 -0.425 \cdot [0.135+0.018]\hspace{0.15cm}\underline {\approx 0} \hspace{0.05cm}.$$

• Ebenso ist auch der Ausgangsimpuls zum Zeitpunkt $t = 3T$ gleich Null:

$$g_3 \ = \ k_0 \cdot g_x(3) +k_1 \cdot [g_x(2)+g_x(4)$$

$$\Rightarrow\hspace{0.3cm}g_3 \ = \ 1.313 \cdot 0.135 -0.425 \cdot [0.368+0.050]\hspace{0.15cm}\underline {\approx 0} \hspace{0.05cm}.$$

• Die Abbildung zeigt,  dass bei diesem exponentiell abfallenden Impuls das Transversalfilter erster Ordnung eine vollständige Entzerrung bewirkt.

• Außerhalb des Intervalls  $-T < t < T$  ist  $g_y(t)$  identisch Null, innerhalb ergibt sich eine Dreieckform.

(4)  Richtig ist nur der  erste Lösungsvorschlag:

• Nachdem bereits mit einem Laufzeitfilter erster Ordnung alle Vor– und Nachläufer kompensiert werden,  ergeben sich auch mit einem Filter zweiter Ordnung und auch für  $N → ∞$  keine weiteren Verbesserungen.

• Dieses Ergebnis gilt  jedoch ausschließlich für den (beidseitig) exponentiell abfallenden Eingansgimpuls.

• Bei fast jeder anderen Impulsform ist das Ergebnis um so besser,  je größer  $N$  ist.