Aufgabe 3.10: Transinformation beim BSC

• Zurück zum Buch

Betrachtetes BSC–Modell

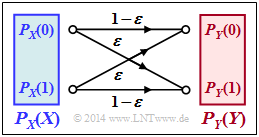
Wir betrachten den  Binary Symmetric Channel  $\rm (BSC)$.  Für die gesamte Aufgabe gelten die Parameterwerte:

• Verfälschungswahrscheinlichkeit:   $\varepsilon = 0.1$,
• Wahrscheinlichkeit für $0$:   $p_0 = 0.2$,
• Wahrscheinlichkeit für $1$:   $p_1 = 0.8$.

Damit lautet die Wahrscheinlichkeitsfunktion der Quelle:   $P_X(X)= (0.2 , \ 0.8)$  und für die Quellenentropie gilt:

$$H(X) = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_0} + p_1\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_1} = H_{\rm bin}(0.2)={ 0.7219\,{\rm bit}} \hspace{0.05cm}.$$

In der Aufgabe sollen ermittelt werden:

• die Wahrscheinlichkeitsfunktion der Sinke:

$$P_Y(Y) = (\hspace{0.05cm}P_Y(0)\hspace{0.05cm}, \ \hspace{0.05cm} P_Y(1)\hspace{0.05cm}) \hspace{0.05cm},$$

• die Verbundwahrscheinlichkeitsfunktion:

$$P_{XY}(X, Y) = \begin{pmatrix} p_{00} & p_{01}\\ p_{10} & p_{11} \end{pmatrix} \hspace{0.05cm},$$

• die Transinformation:

$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm},$$

• die Äquivokation:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \big ] \hspace{0.05cm},$$

• die Irrelevanz:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \big ] \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Anwendung auf die Digitalsignalübertragung.
• Bezug genommen wird insbesondere auf die Seite  Transinformationsberechnung für den Binärkanal.
• In der  Aufgabe 3.10Z  wird die Kanalkapazität  $C_{\rm BSC }$  des BSC–Modells berechnet.
• Diese ergibt sich als die maximale Transinformation  $I(X;\ Y)$  durch Maximierung bezüglich der Wahrscheinlichkeiten  $p_0$  bzw.  $p_1 = 1 - p_0$.

Fragebogen

1

Berechnen Sie die Verbundwahrscheinlichkeiten  $P_{ XY }(X, Y)$

$P_{ XY }(0, 0) \ = \ $

$P_{ XY }(0, 1) \ = \ $

$P_{ XY }(1, 0) \ = \ $

$P_{ XY }(1, 1) \ = \ $

2

Wie lautet die Wahrscheinlichkeitsfunktion  $P_Y(Y)$  der Sinke?

$P_Y(0)\ = \ $

$P_Y(1) \ = \ $

3

Welcher Wert ergibt sich für die Transinformation  $I(X;\ Y)$?

$I(X; Y)\ = \ $ $\ \rm bit$

4

Welcher Wert ergibt sich für die Äquivokation  $H(X|Y)$?

$H(X|Y) \ = \ $ $\ \rm bit$

5

Welche Aussage trifft für die Sinkenentropie  $H(Y)$  zu?

	$H(Y)$  ist nie größer als  $H(X)$.
	$H(Y)$  ist nie kleiner als  $H(X)$.

6

Welche Aussage trifft für die Irrelevanz  $H(Y|X)$  zu?

	$H(Y|X)$  ist nie größer als die Äquivokation  $H(X|Y)$.
	$H(Y|X)$  ist nie kleiner als die Äquivokation  $H(X|Y)$.

Musterlösung

Musterlösung

(1)  Für die gesuchten Größen gilt allgemein bzw. mit den Zahlenwerten  $p_0 = 0.2$  und  $\varepsilon = 0.1$:

$$P_{XY}(0, 0) = p_0 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.18} \hspace{0.05cm}, \hspace{0.5cm} P_{XY}(0, 1) = p_0 \cdot \varepsilon \hspace{0.15cm} \underline {=0.02} \hspace{0.05cm},$$

$$P_{XY}(1, 0) = p_1 \cdot \varepsilon \hspace{0.15cm} \underline {=0.08} \hspace{0.05cm}, \hspace{1.55cm} P_{XY}(1, 1) = p_1 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.72} \hspace{0.05cm}.$$

(2)  Allgemein gilt:

$$P_Y(Y) = \big [ {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1) \big ] = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon & \varepsilon\\ \varepsilon & 1 - \varepsilon \end{pmatrix}.$$

Daraus ergeben sich folgende Zahlenwerte:

$${\rm Pr}( Y = 0)= p_0 \cdot (1 - \varepsilon) + p_1 \cdot \varepsilon = 0.2 \cdot 0.9 + 0.8 \cdot 0.1 \hspace{0.15cm} \underline {=0.26} \hspace{0.05cm},$$

$${\rm Pr}( Y = 1)= p_0 \cdot \varepsilon + p_1 \cdot (1 - \varepsilon) = 0.2 \cdot 0.1 + 0.8 \cdot 0.9 \hspace{0.15cm} \underline {=0.74} \hspace{0.05cm}.$$

(3)  Für die Transinformation gilt gemäß der Definition mit  $p_0 = 0.2$,  $p_1 = 0.8$  und  $\varepsilon = 0.1$:

$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \hspace{-0.05cm}\cdot \hspace{-0.05cm} P_{Y}(Y) }\right ] \hspace{0.3cm} \Rightarrow$$

$$I(X;Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.18}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.02 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.02}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} + 0.08 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.08}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.72 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.72}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} \hspace{0.15cm} \underline {=0.3578\,{\rm bit}} \hspace{0.05cm}.$$

(4)  Mit der angegebenen Quellenentropie  $H(X)$  erhält man für die Äquivokation:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(X) - I(X;Y) = 0.7219 - 0.3578 \hspace{0.15cm} \underline {=0.3642\,{\rm bit}} \hspace{0.05cm}.$$

• Man könnte aber auch die allgemeine Definition mit den Rückschlusswahrscheinlichkeiten  $P_{X|Y}(⋅)$  anwenden:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \hspace{0.05cm}\right ] = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{P_Y(Y)}{P_{XY} (X, Y)} \hspace{0.05cm} \right ] \hspace{0.05cm}$$

• Im Beispiel erhält man auch nach dieser Berechnungsvorschrift das gleiche Ergebnis  $H(X|Y) = 0.3642 \ \rm bit$:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.18} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.02} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.08} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.72} \hspace{0.05cm}.$$

(5)  Richtig ist der Lösungsvorschlag 2:

• Bei gestörter Übertragung  $(ε > 0)$  ist die Unsicherheit hinsichtlich der Sinke stets größer als die Unsicherheit bezüglich der Quelle.  Man erhält hier als Zahlenwert:

$$H(Y) = H_{\rm bin}(0.26)={ 0.8268\,{\rm bit}} \hspace{0.05cm}.$$

• Bei fehlerfreier Übertragung  $(ε = 0)$  würde dagegen  $P_Y(⋅) = P_X(⋅)$  und  $H(Y) = H(X)$  gelten.

(6)  Auch hier ist der zweite Lösungsvorschlag richtig:

• Wegen  $I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)$  ist  $H(Y|X)$  um den gleichen Betrag größer als  $H(X|Y)$, um den  $H(Y)$  größer ist als  $H(X)$:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) -I(X;Y) = 0.8268 - 0.3578 ={ 0.4690\,{\rm bit}} \hspace{0.05cm}$$

• Bei direkter Berechnung erhält man das gleiche Ergebnis  $H(Y|X) = 0.4690\ \rm bit$:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \right ] = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} \hspace{0.05cm}.$$